Molekula

Dio molekule DNK.

Kalotni model molekule vode, molekulske formule H₂O.

Slika pretražnog mikroskopa s tuneliranjem molekule pentacen, koja se sastoji od linearnih lanaca od 5 ugljikovih prstenova.

AFM (eng. Atomic Force Microscopy) molekule PTCDA, u kojoj je vidljivo 5 prstena sa 6 ugljikovih atoma.

AFM slika 1,5,9-triokso-13-azatriangulena i njegove kemijske strukture.

Model kuglica-štapić molekule metanola.

Strukturna formula metana.

Temperatura idealnog plina je mjera prosječne kinetičke energije molekula.

Gay-Lussacov zakon za stalan tlak.

Molekula (novolat. molecula: mala masa, od lat. moles: masa) je najmanja elementarna čestica neke jednostavne ili složene čiste kemijske tvari koja još ima za tu tvar karakteristična kemijska svojstva. Molekula se sastoji od atoma, među sobom jednakih u elementarnim tvarima, a različitih u kemijskim spojevima. Molekula je u načelu električki neutralna, sa sparenim brojem elektrona, iako se katkad molekulama smatraju i ioni i slobodni radikali (koji su električno nabijeni). Atome u molekuli drže na okupu kemijske veze. Broj atoma u molekuli može biti vrlo različit, tako na primjer molekula kisika sastoji se od 2 atoma (O₂), ugljikova dioksida od 3 atoma (CO₂) i tako dalje, sve do više milijuna atoma (na primjer molekule virusa). Molekularna formula pokazuje koji atomi i u kojem omjeru tvore molekulu, a iz toga slijedi i relativna molekularna masa. Način povezivanja atoma u molekuli prikazuje strukturna formula, a prostorni smještaj atoma u molekuli stereokemijska formula (kemijska formula).

Veličina molekule ovisi o broju, vrsti i rasporedu atoma i većinom je u granicama između od 0,1 do 10 nanometara, dok je masa obično između 10^–24 i 10^–20 grama. Masa golemih molekula (makromolekula), koje se katkad mogu vidjeti elektronskim mikroskopom, mnogo je veća (oko 10^–18 grama). Postojanje manjih molekula očituje se u mnogim pojavama kao što su difuzija, Brownovo gibanje, volumni odnosi pri spajanju plinova, toplinsko zračenje, raspršenje svjetlosti u atmosferi, ogib ili difrakcija rendgenskih zraka i drugo. Podrobni podatci o strukturi molekula pokusima (eksperimentalno) se dobivaju njihovim međudjelovanjem s elektromagnetskim zračenjem (spektroskopija)

O postojanju molekula može se govoriti samo ako postoje određene (definirane) skupine atoma koje se na okupu drže silama dovoljno jakima da se ta skupina može smatrati jedinkom. Tako su građeni spojevi u kojima su atomi povezani kovalentnim vezama, ponajprije većina organskih spojeva, plinovi (osim plemenitih plinova) i drugo. Nasuprot tomu, u mnogim kristaliziranim anorganskim tvarima (metali i njihove soli) svi su atomi međusobno povezani ionskim ili metalnim vezama pa nema izdvojenih atomskih skupina koje bi se mogle smatrati jedinkama i imati svojstva molekula. Kemijska formula u takvom slučaju pokazuje samo kemijski sastav tvari, odnosno formulsku jedinku (kemijska veza). Ima i primjera kada molekule određena sastava postoje u čvrstom i kapljevitom stanju, ali ne postoje u plinovitom stanju (jer se pri isparavanju raspadaju), ili postoje u čvrstom stanju ali se, prelazeći u kapljevito stanje, raspadaju (na primjer većina kompleksnih spojeva). Kemijska svojstva mnogih tvari određena su najvećim dijelom sastavom i strukturom njihovih molekula. Golem broj pojava i procesa u prirodi i industriji povezan je stoga s postojanjem i pretvorbama molekula i s reakcijama među njima. Molekule postoje i u međuzvjezdanoj tvari u obliku golemih molekularnih oblaka koji se mogu prepoznati po svojstvenim emisijskim linijama u radiofrekvencijskom spektralnom području.

Postojanje molekula prvi je spoznao talijanski fizičar i kemičar A. Avogadro (1811.), ali je pravu razliku između atoma i molekula objasnio gotovo 50 godina poslije talijanski kemičar S. Cannizzaro.

Među molekulama postoje međumolekularne sile, na primjer poznate Van der Waalsove sile, koje su u plinovima vrlo slabe (silama te vrste objašnjava se na primjer odstupanje realnih plinova od vladanja idealnoga plina), ali su u mnogim kapljevinama i čvrstim tvarima dovoljno jake da molekule drže na okupu, iako su bitno slabije od kemijskih veza.

Znanost biologije koja se bavi molekulama naziva se molekularna biologija.

Povijest

Naziv molekula prvi je uporabio A. Avogadro 1811. u želji da objasni ponašanje plinova u kemijskim reakcijama. Pretpostavio je da su najmanje čestice plinova nakupine atoma koje je nazvao molekule. Ta ideja je zatim pala u zaborav ali ju je obnovio S. Cannizzaro 1858. od kada je općenito prihvaćena.

Građa molekula

Molekula se može sastojati od atoma istog elemenata ili od atoma više različitih elemenata. Primjerice, dušikova molekula N₂ sastoji se od dva atoma dušika. S druge strane, molekula vode H₂O sastoji se od dva atoma vodika i jednog atoma kisika. Molekule jednog elementa javljaju se isključivo u nemetala, i to obično dva atoma po molekuli. Neki se nemetali, poput kisika, fosfora, sumpora mogu pojaviti u molekulama od različitog broja atoma. To se svojstvo zove alotropija.

Veličina molekula

Molekule su premale da bi se vidjele golim okom, pa čak ni elektronskim mikroskopom. Duljina kovalentne veze najmanje molekule (H₂) iznosi 74 pm (74•10^-12 m). Njihov promjer obično iznosi od 0,1 do 100 nanometara (10^-9 m). Međutim duljina molekula može biti puno veća, poput makromolekule DNK. Kada bi se jedna DNK izvadila iz stanične jezgre i razmotala, dosezala bi duljinu od jednog do dva metra. No, i tada bi bila nevidljiva jer bi njezino vlakno bilo debelo svega 5 nm. Zato se za određivanje veličine i oblika molekula primjenjuju posebne metode fizikalne kemije, uglavnom instrumentalne prirode.

Relativna molekulska masa je zbroj masa atoma koji čine molekulu. Kao i atomska masa, molekulska masa se izražava u atomskim jedinicama mase (u = 1/12 mase ugljikova izotopa ¹²C). Masa najmanje molekule H₂ iznosi m(H₂) = 3,346•10^-24 g ili 3,346•10^-27 kg. Makromolekule mogu imati na stotine tisuća atoma ali i tada su to teško zamislive male mase.

Dugo se vjerovalo da su duljine kemijskih veza i njihovi prostorni kutovi u molekuli konstantni, ali novija istraživanja ukazuju na njihovu neznatnu promjenjivost, posebice kod složenijih molekula.

Molekule opisujemo formulama

Odnos elemenata koji grade molekule izražava se empirijskom formulom. Na primjer, vodik i kisik grade vodu u najmanjem omjeru 2:1 zato formula H₂O istovremeno predstavlja empirijsku i molekulsku formulu. Ugljik, vodik i kisik grade etanol u omjeru 2:6:1 (C₂H₆O). Ovaj omjer ne mora nužno određivati samo jednu jedinstvenu molekulu — dimetil eter ima isti omjer kao etanol, no nema istu molekularnu strukturu. Takve se molekule zovu izomeri. Sažeta strukturna formula točnije određuje raspored atoma u molekuli, pa je tako formula etanola CH₃–CH₂–OH, a formula dimetil etera CH₃–O–CH₃. Za predstavljanje složenijih molekula, gdje atomi mogu biti raspoređeni u prostoru na različite načine, rabi se strukturna formula.

Osim formulama molekule se prikazuju modelima koji mogu biti kalotni ili kuglica-štapić.

Atomska teorija tlaka i specifične topline

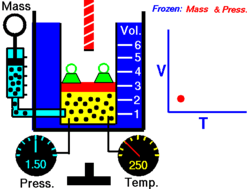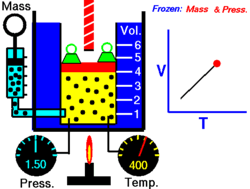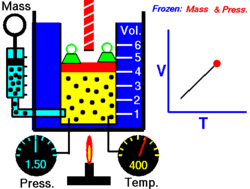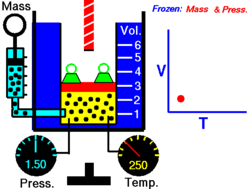
Prema atomističkim predodžbama tlak plina uzrokovan je udarcima molekula o zid posude. Da pojednostavimo stvarne odnose, pretpostavit ćemo da se u kocki sve molekule kreću istom brzinom. Dalje možemo zamisliti da se jedna trećina molekula kreće gore-dolje, druga trećina lijevo-desno, a ostatak naprijed-nazad. Prema svakom zidu kocke kreće se dakle 1/6 svih molekula. Pri udaru o zid promijeni se smjer brzine. Ima li molekula prije sraza impuls sile p + m∙v, to poslije odbijanja (refleksije) ima impuls - m∙v. Odbijanjem od zida promijeni se impuls molekula za 2∙m∙v. Toliki impuls preuzme zid kocke. Mnogobrojni udari molekula očituju se kao neprekinuti (kontinuirani) tlak plina. Tlak plina je pritisak (sila) na jedinicu površine. Sila je po Newtonovom zakonu gibanja jednaka promjeni impulsa sile u jedinici vremena. Tlak plina dobivamo dakle, tako da proračunamo, koliki impulsi prenesu molekule u jednoj sekundi na 1 m² zida.

Očito je da će na 1 m² zida kocke u jednoj sekundi udariti one molekule koje se nalaze pred zidom u stupcu koji je dug upravo toliko, kolika je brzina molekula. Broj molekula u 1 m³ označit ćemo sa n. U stupcu dugom v s presjekom od 1 m² nalazi se n∙v. Jedna šestina tih molekula kreće se prema zidu i prenese u sekundi na zid impuls jednak:

$p={\frac {1}{6}}\cdot n\cdot v\cdot 2\cdot m\cdot v={\frac {1}{3}}\cdot n\cdot m\cdot v^{2}$

To je tlak plina. Vidi se, da je tlak plina dan brojem molekula u 1 m³ i njihovom kinetičkom energijom 1/2∙m∙v². To je vrlo razvidan rezultat. Gornju jednadžbu možemo još pisati u drugom obliku, da za n stavimo omjer između L - broja molekula u molu i V - volumena mola:

$p\cdot V={\frac {1}{3}}\cdot L\cdot m\cdot v^{2}$

Tlak na zid kocke opažamo kao stalan tlak, iako je on uistinu posljedica isprekidanih udaraca molekula. Ta kontinuiranost tlaka je znak da se plin sastoji od vrlo velikog broj molekula. Mnoštvo sitnih molekula proizvodi učinke, koji se u makroskopskim dimenzijama očituju kao kontinuirane osobine ili trajne sile.

U teorijskoj jednadžbi možemo po Gay-Lussacovu zakonu umnožak p∙V zamijeniti sa R∙T. Tada dobivamo jednadžbu:

$R\cdot T={\frac {1}{3}}\cdot L\cdot m\cdot v^{2}$

Odatle dobivamo za kvadrat brzine izraz:

$v^{2}={\frac {3\cdot R\cdot T}{L\cdot m}}$

Broj i masa molekula zasad su nepoznate, ali je njihov umnožak iskustveno ustanovljena veličina. L∙m je masa jednog mola plina. Kako se razabire, brzina je dana samim poznatim veličinama. Po toj jednadžbi izračunate su brzine molekula kod temperature ledišta vode za različite plinove:

Brzine molekula

Plin	Masa mola (g)	Brzina (m/s)
Vodik	2	1 840
Dušik	28	490
Kisik	32	460
Radon	222	170

Da bi se ispitala ispravnost atomske teorije, morale su se pokusima odrediti brzine molekula. Taj zadatak je pokusima riješio O. Stern 1920. On je pomoću električne struje ugrijao nit srebra tako da je isparivala atome. Atome je pustio da jure u evakuiranoj staklenoj cijevi.

Otvorima na uzastopnim zastorima atomi su se u cijevi izdvojili u homogeni snop. Takvu se snopu vrlo točno mogla izmjeriti brzina. Čitava se aparatura stavila u brzu vrtnju. Atomi srebra zbog toga nisu na ploči pali točno iza otvora na zastoru, nego malo više prema gore. Taj pomak dan je vremenom što ga atom srebra treba da bi prošao razmak od zastora do ploče. Tako izmjerene brzine molekula potpuno su se slagale s teorijom.

Energija plina dana je zbrojem kinetičkih energija svih molekula. Kinetička energija pojedine molekule jednaka je 1/2∙m∙v², a cjelokupna energija mola umnošku 1/2∙L∙m∙v². Energiju mola dakle dobivamo da gornju atomističku jednadžbu pomnožimo sa 3/2. Učinivši to, dobivamo za energiju U mola plina:

$U={\frac {3}{2}}\cdot R\cdot T$

Energija je u bitnom dana umnoškom plinske konstante i temperature. Taj zaključak teorije može se pokusima točno provjeriti. Energiju plina možemo povećati ili umanjiti tako, da plin grijemo ili hladimo. Prema gornjoj jednadžbi, specifična toplina plina jednaka je:

$C_{V}={\frac {3}{2}}\cdot R$

Ova teorijska vrijednost vrlo se dobro slaže s mjerenjem na jednoatomnim plinovima, kao što su helij, neon, argon i tako dalje. Za druge plinove, gdje su molekule građene od dva ili više atoma, daju mjerenja veće vrijednosti. To je jasno ako pomislimo da energija višeatomnih molekula može biti sadržana i u vrtnji atoma oko unutarnjih osi, a ne samo u prostornom gibanju molekula kroz prostor. Specifične topline višeatomnih plinova proračunat će se kasnije.

Taj primjer lijepo osvjetljuje kako atomistička teorija povezuje različita svojstva materije. Na plinsku konstantu R ispitivači su nadošli ispitujući tlak plinova. U početku se nije očekivalo da će postojati neka uska veza između plinske konstante i energije plina. Atomistika ujedinjuje energetsko ponašanje plinova s njihovim napetostima. Takvo povezivanje različitih osobina materije u izraz jedinstvene stvarnosti je glavna crta atomske teorije.

Što je niža temperatura plina, to su polaganija gibanja molekula. na apsolutnoj nuli nastupa potpuno mirovanje. Jasno je da se ispod te temperature materija ne može ohladiti. Hlađenje se sastoji u oduzimanju kinetičke energije molekula. No kad sve molekule miruju, ne može se više ništa energije oduzeti. Materija se nalazi u stanju najniže energije. To je puno fizičko značenje apsolutne nule temperature.

Dijeleći ukupnu energiju mola Avogadrovim brojem L, dobivamo prosječnu energiju čestice u plinu:

$U={\frac {3}{2}}\cdot k\cdot T$

$k={\frac {R}{L}}$

gdje je: k - Boltzmannova konstanta, koja se može izračunati, čim je Avogadrov broj određen (broj molekula u molu).

Vrtnje molekula i specifična toplina

Pored pravocrtnog (translacijskog) gibanja mogu se molekule okretati i oko sebe samih. Energija vrtnje ili rotacijska energija zavisi također od temperature te daje svoj doprinos specifičnoj toplini plina. Molekulu možemo shvatiti kao kruto tijelo, jer atomi imaju stalne međusobne razmake. S obzirom na to da nema vanjskih sila, težište molekule kreće se s konstantnom brzinom. To gibanje zasad nas ne zanima i pretpostavit ćemo da težište molekule miruje. Molekula se vrti oko neke čvrste osi koja prolazi kroz težište. Općenito se rotacijska energija dobije iz pravocrtnog gibanja tako da se masa zamijeni momentima tromosti s obzirom na glavne osi, a komponente impulsa p_x, p_y i p_z komponentama momenta impulsa. Prema tome, za prosječnu rotacijsku energiju dobivamo iste izraze kao i za pravocrtno gibanje. Na svaki stupanj slobode otpada prosječna energija 1/2∙k∙T. Prosječna rotacijska energija molekule jednaka je:

$E_{rot}={\frac {3}{2}}\cdot k\cdot T$

Energija molekule plina zbroj je kinetičke i rotacijske energije:

$E=E_{kin}+E_{rot}={\frac {3}{2}}\cdot k\cdot T+{\frac {3}{2}}\cdot k\cdot T=3\cdot k\cdot T$

Pomnoživši to Avogadrovim brojem L, dobivamo energiju jednog mola plina:

$U=3\cdot L\cdot k\cdot T=3\cdot R\cdot T$

Iz ove jednadžbe proizlazi da je specifična toplina (kod konstantnog volumena) jednaka:

$C_{V}=3\cdot R$

To se slaže s pokusima i mjerenjima. Odstupanje se opaža za plinove sastavljene od dvoatomnih molekula. Tamo, čini se, otpada vrtnja oko one osi koja prolazi kroz obje molekule. S obzirom na tu os moment tromosti molekule gotovo isčezava. Time imamo stupanj slobode manje. Prosječna energija dvoatomne molekule nije jednaka 6∙1/2∙k∙T, nego 5∙1/2∙k∙T. Za specifičnu toplinu dvoatomnih plinova dobivamo:

$C_{V}={\frac {5}{2}}\cdot R$

prema starim mjernim jedinicama, R je približno 2 cal/°C. Specifična toplina višeatomnih plinova iznosi dakle po teoriji 6 cal/°C, a dvoatomnih plinova 5 cal/°C. Ove vrijednosti izvrsno se slažu s iskustvom.

Od kinetičke energije molekula zavisi u kakvom se agregatnom stanju nalazi materija. Dok se molekule kreću s velikim brzinama, bez važnosti su međusobne sile molekula. Svaka molekula juri kroz prostor nezavisno o stanju. Za velike kinetičke energije molekula materija se nalazi u plinskom stanju. Da plin pretvorimo u tekućinu moramo molekulama oduzeti mnogo energije. Plin postaje tekućina ako ga ohladimo na određenu nisku temperatura. Na toj niskoj kritičnoj temperaturi molekule ostaju sve duže jedna uz drugu pa se počinju gomilati u male hrpe. Postepenim oduzimanjem kinetičke energije plin postaje tekućina. U tekućini molekule kližu jedna uz drugu. Materija je zadobila stalnu gustoću.