Brownovo gibanje


Brownovo gibanje je nasumično gibanje čestica koje su mnogo veće nego atomi i obične molekule, ali premalene da bi bile vidljive golim okom u nekom fluidu, kao primjerice gibanje čestica dima u zraku ili peludnih čestica u vodi. Škotski botaničar Robert Brown otkrio je oko 1820. s pomoću mikroskopa da se čestice peluda raspršene u tekućini neprekidno nasumce gibaju amo-tamo. Ta je pojava po njemu nazvana Brownovo gibanje. Ona je izravan dokaz molekularno-kinetičke teorije. Prema toj teoriji molekule fluida neprestano se nasumce gibaju, udaraju u čestice koje se vide mikroskopom i potiskuju ih amo-tamo. Konačan rezultat sudara s molekulama fluida gibanje je čestice po izlomljenoj crti. Što su veće te čestice, manja je razlika između broja molekula koje su se sudarile s česticama s pojedinih strana i to se manje ističe njihovo Brownovo gibanje. Ono se i ne opaža za čestice dovoljno velike da se vide golim okom. Promjer čestica koje pokazuju intenzivno Brownovo gibanje je oko 10–7 do 10–6 metara, što je približno tisuću puta više od promjera molekula. Teoriju Brownova gibanja razvio je Albert Einstein 1905. godine. Godine 1908. Jean Baptiste Perrin pokusom s pomoću Brownova gibanja odredio je vrijednost Avogadrovog broja i tim pokusima potvrdio atomsku građu tvari. [1]
Uvod
Kao što znamo, čestice se fluida kreću potpuno kaotično, zbog čega primjerice ne možemo predvidjeti ponašanje kapljice tinte u čaši vode. Ako u neki fluid stavimo neko veliko tijelo, promjera na primjer 50 cm, čestice će fluida na to tijelo djelovati potpuno jednoliko, zbog velikog broja čestica koje se u svakom trenutku sudaraju s tijelom. No, ako umjesto tog tijela u fluid stavimo mnogo manje tijelo koje je od čestica fluida veće do nekoliko tisuća puta (na primjer zrnce peluda u vodu), čestice će se fluida sudarati s tim tijelom neravnomjerno, te će se ono pod utjecajem njihove kinetičke energije polako kretati u potpuno kaotičnom režimu, nestalnog smjera i brzine. Gibanje tog tijela zove se Brownovo gibanje.
Povijest
Jan Ingenhousz je opisao nepravilno gibanje čestica ugljene prašine na površini alkohola 1785.. Pa ipak, otkriće se Brownovog gibanja tradicionalno pripisuje Robertu Brownu, 1827. Vjeruje se da je Brown mikroskopirao čestice peluda kako plutaju u vodi. Nakon toga promatrao je sićušne čestice unutar vakuola zrna peluda koje se kreću "drhtavo". No, uzrok takvog gibanja još nije imao objašnjenje.
Torvald N. Thiele 1880. je godine prvi matematički opisao Brownovo gibanje. Nezavisno od toga, Louis Bachelier je 1900. učinio isto u svom doktoratu. No, Albert Einstein je 1905. došao do odgovora i time pokazao da je Brownovo gibanje način da se indirektno potvrdi postojanje atoma i molekula.
U to vrijeme atomska priroda tvari još uvijek nije bila priznata. Einstein i Marian Smoluchowski primijetili su da, ako je kinetička teorija fluida točna, molekule vode bi se gibale nasumično. Dakle, mala bi se čestica slučajnom snagom iz slučajnog smjera sudarila sa slučajnim brojem molekula vode u nekom kratkom vremenskom intervalu. Takvo bi sudaranje molekula vode s dovoljno malom česticom prouzrokovalo jednako gibanje čestice kakvo je opisao Brown. Theodor Svedberg je demonstrirao Brownovo gibanje u koloidima, a Felix Ehrenhaft s česticama srebra u zraku. Jean Baptiste Perrin proveo je pokuse kojima je ispitao nove matematičke modele te su njegovi rezultati konačno, nakon 2000 godina raspravâ, dokazali postojanje atoma i molekula.
Fraktalna svojstva
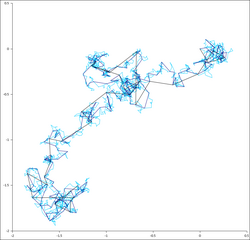
Ako Brownovo gibanje preslikamo na graf, dobit ćemo fraktalnu strukturu. Fraktalnu strukturu možemo promatrati ako za različite iteracije uzmemo grafove u kojima je položaj čestice označen u različitim vremenskim intervalima (te su položaji spojeni ravnim crtama). Na slici desno vidimo tri "iteracije". Povećavanjem nekog dijela druge iteracije dobit ćemo strukturu koja uvelike sliči strukturi prve iteracije, i tako unedogled. Treba primijetiti da ove strukture nisu potpuno samoslične, nego se neka njihova svojstva ne mijenjaju sa stupnjem povećanja. Drugim riječima, ako pogledamo graf nekog Brownovog gibanja na području od 100 cm2 kroz vrijeme od 100 s i graf na području od 1 cm2 kroz vrijeme od 1 s, nećemo ni na koji način moći prepoznati koji graf označava koje vrijeme promatranja (i koju površinu). Kao i svi ostali stohastični fraktali, ovi se fraktali odlikuju samo svojstvom da njihova fraktalna dimenzija pri svakom uvećanju ostaje ista.