Auguste Bravais
| Auguste Bravais | |
| Pogreška pri izradbi sličice: | |
| Rođenje | 23. kolovoza 1811. Annonay, Ardèche, Francuska |
|---|---|
| Smrt | 30. ožujka 1863. Le Chesnay, Yvelines, Francuska |
| Narodnost | Francuz |
| Polje | Kristalografija |
| Institucija | Politehnička škola u Parizu |
| Alma mater | Politehnička škola u Parizu |
| Poznat po | Bravaisove ili translacijske rešetke |
<templatestyles src="Multiple image/styles.css" wrapper=".tmulti"></templatestyles>


Auguste Bravais (Annonay, 23. kolovoza 1811. – Le Chesnay, 30. ožujka 1863.), francuski fizičar i mineralog . U okviru hipoteze, koju je razradilo nekoliko matematičara i fizičara, i po kojoj se kristali sastoje od najsitnijih, pravilno trodimenzionalno periodički razmještenih čestica koje stvaraju prostornu rešetku, Bravais je 1848. dokazao da 14 tipova prostornih rešetaka (danas ih zovemo i Bravaisove ili translacijske rešetke) pokriva sve tipove periodičkog ponavljanja čestica u kristalnim strukturama. Godine 1912. njemački fizičar M. Laue potvrdio je njegovu teoriju. [1]
Kristalna struktura čvrstog tijela
U prirodi se često nalaze komadići materije, koji su omeđeni ravnim plohama i predstavljaju pravilna geometrijska tijela kao kocke, piramide, oktaedre i tako dalje. Proučavanje takvih pravilnih kristala već je odavno jedan od osnovnih zadataka mineraloga, a matematičari su našli poticaja u kristalima da nauku o simetrijama razviju do vrlo visokog stupnja. Duboko fizičko značenje dobilo je ispitivanje kristala tek modernom atomnom teorijom. Činjenice o kristalima nesumljivo govore da je to prototip sastava čvrstog tijela. Čvrsti oblik materije osniva se na kristalnoj strukturi. Ako je komadić čvrste materije jedan kristal, tad se pravilni oblik razabire na prvi pogled. No ako se čvrsto tijelo sastoji od mnogo sitnih kristala, koji su poredani u svim mogućim smjerovima, tad je simetrija strukture izbrisana za naše oko.
Već u 18. stoljeću je naslutio R. J. Haüy, da je pojava kristala uzrokovana pravilnim rasporedom osnovnih djelića. Zamislimo li te djeliće kao kocke, možemo njima izgraditi razna geometrijska tijela. Haüyev model kristala usavršio je A. Bravais 1848. On se oslobodio naivnih predodžbi o kompaktnim djelićima i uzeo, da su težišta molekula poredana u pravilnim geometrijskim razmacima. Ona čine kristalnu rešetku. Opću sistematiku kristalnih rešetaka razvili su 1891. J. S. Fjodorov i Arthur Moritz Schoenflies (1853. - 1928.).
Za kristal je svojstveno da se određeni raspored molekula periodički ponavlja u prostoru. Promatrat ćemo najprije jednostavnu kristalnu rešetku koja je građena od samih jednakih atoma ili molekula. Onaj određeni raspored molekula koji se ponavlja u prostoru obuhvatimo u jednu elementarnu ćeliju. Paralelnim pomakom ćelije u sva tri prostorna smjera možemo izgraditi čitavu rešetku. Tip rešetke možemo prema tome jednoznačno utvrditi elementarnom ćelijom.
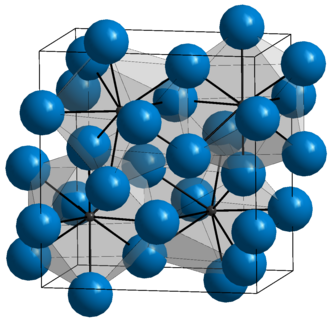
Najjednostavniju elementarnu ćeliju predstavlja kocka koja u svakom kutu sadrži jedan atom ili molekulu. Takva ćelija zove se još prosta kubna. Nešto složenija je ćelija koja u centru kocke sadrži još jedan atom ili molekulu. Takvu kubičnu rešetku s prostornim centrima imaju kristali alkalijskih metala (Li, Na, K, Rb, Cs), zatim vanadij V, krom Cr, molibden Mo, tantal Ta i neki drugi. Mjesto u prostornom centru kocke može po jedan atom stajati u centru svake stranice. Kubne rešetke s takvim plošnim centrima također su česte u prirodi. Tako se kristaliziraju kemijski elementi srebro Ag, zlato Au, platina Pt, bakar Cu, olovo Pb i drugi.
Svakom kristalu pripadaju 3 glavne osi smjera ili osi. Ako je elementarna ćelija kocka, tada su osi među sobom okomite. Općenito mogu osi kristala zatvarati kutove različite od 90°. Elementarnu ćeliju možemo općenito opisati s 3 vektora , i , koji određuju bridove ćelije. Čvor ove jednostavne rešetke dobijemo tako da vektore , i nanesemo cijeli broj puta. Točke rešetke su dane sa:
gdje n1, n2 i n3 mogu poprimiti sve cijele brojeve. Pomakom rešetke u glavnim smjerovima za veličinu , ili ne mijenja se raspored molekula u prostoru. Ta invarijantnost prema prostornim pravocrtnim pomacima (translacijama) osnovna je simetrija kristala.
Jednostavna rešetka izgrađena je od jednakih atoma ili jednakih atomskih grupa. Svaki atom ili svaka atomska grupa na isti su način opkoljeni od drugih atoma ili atomskih grupa. Nijedan atom ne ističe se ničim ispred drugog. Ako se kristal sastoji od različitih atoma ili više vrsta atomskih grupa, tad svaka čini za sebe jednu jednostavnu rešetku. Kristal je složena rešetka. U takvom kristalu opet svaki atom ili svaka ista atomna grupa ima istu okolinu, ali različiti atomi opkoljeni su različitim rasporedom atoma.
Najjednostavniju složenu rešetku čine kristali kuhinjske soli. Atomi natrija i klora poredani su u 3 okomita smjera u jednakim razmacima. Da su atomi jednaki, imali bismo prostu kubnu rešetku. Budući da nisu jednaki, moramo kristal NaCl sastaviti od dvije jednostavne kubne rešetke s plošnim centrima. Vidi se da je svaki natrijev atom opkoljen sa 6 klorovih atoma, i obratno, svaki klorov sa 6 natrijevih atoma. Kod kristala od mnogo različitih elemenata simetrije su mnogo složenije. Tek odabranim geometrijskim rasporedom može se postići da jednaki atomi budu opkoljeni istovrsnom skupinom drugih atoma. Po osnovnom načelu simetrije moraju jednaki atomi imati jednaku okolinu; ničim ne smije biti jedan isti atom istaknut pred drugim istim atomom.
Matematičari su općenito ispitivali koji su kristalni oblici mogući po zakonu simetrije. Matematička disciplina, teorija grupa, pruža općenito pregled nad svim mogućim kristalnim oblicima. Najveći broj matematičkih simetrija je zaista nađen kod stvarnih kristala u prirodi. Svaka kristalna mreža u prirodi odgovara jednoj matematički mogućoj simetriji. Nikada se još nije naišlo na kristale koji bi se protivili zakonu simetrije. Simetrija kristalnih oblika jedan je od najdubljih prirodnih zakona. Simetrija proniče čitavu prirodu, savršeno u njenim najsitnijim dijelovima, a djelomično u njenim makroskopskim oblicima. Stvarajući pravilne geometrijske likove, čovjek je samo oponašao prirodu, koja je upravo neiscrpna u stvaranju raznih simetričnih oblika. Simetrije, koje je narod dugogodišnjim radom razvio u ornamentici, one lijepe oblike na vezovima, nalazimo i u prirodi. Atomni sistemi poprimaju nužno izvjesne simetrije, oni iz samih sebe proizvode uvijek nove i uvijek ljepše oblike. Simetrija je najljepši izraz duboke harmonije i zakonitosti koje vladaju u atomnim procesima.
Sva svojstva čvrstog tijela određena su kristalnom rešetkom. Ako se jedan element javlja u dvije različite modifikacije, tad se njegovi atomi na dva različita načina raspoređuju u rešetke. Premda su na primjer dijamant i grafit građeni od jednakih ugljikovih atoma, oni se ipak u osnovi razlikuju čemu je uzrok različita struktura kristalne rešetke.
Ispitivanje rendgenskim zrakama dalo je uvid u strukturu kristala. Iz rendgenskih slika utvrđene su elementarne ćelije pojedinih kristala. Zasad ćemo samo iznijeti, da hipoteza o rešetki objašnjava sva svojstva čvrstog stanja materije. Poznato je, da postoji izvjesna anizotropija u elastičnim i optičkim svojstvima kristala. Postojanje triju glavnih osi obzirom na prolaz svjetlosti ili deformaciju čvrstog tijela objašnjava se s tri glavna smjera kristalne rešetke. Samo kod apsolutne nule miruju atomi u čvorovima rešetke. Titranjem molekula ili atoma oko položaja mogu se objasniti sva akustična i toplinska svojstva čvrstih tijela.
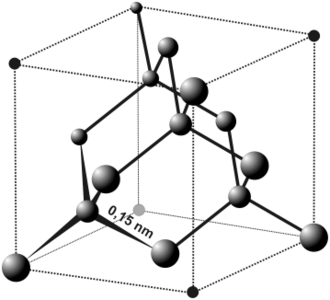
Na kraju nameće se pitanje: koliki su razmaci između atoma ili molekula u kristalnoj rešetki? Razmake možemo proračunati kad znamo vrstu elementarne ćelije i broj atoma u m3. Uzmimo da se kemijski element, što je često slučaj, kristalizira u kubnoj rešetki s prostornim centrom. Volumen ćelije jednak je a3, gdje je a stranica kocke. Svakoj elementarnoj ćeliji pripadaju dva atoma. Jedan daje prvi ugao kocke, a drugi je centar kocke. Na svaki atom, otpada polovina volumena ćelije:
gdje je: V - volumen koji otpada na jedan atom, pomnožen sa N, brojem atoma u 1 m3, daje 1:
Broj atoma u 1 m3 odnosi se prema broju atoma u jednom molu L kao gustoća ρ prema masi mola M:
Uzmemo li u obzir sva tri odnosa, dobivamo da je razmak između atoma u kubnoj rešetki s prostornim centrima jednak:
Težinu mola, kao i specifičnu težinu, poznajemo za svaki kemijski element, pa odatle možemo proračunati razmak između atoma rešetke. U donjoj tablici su dane vrijednosti za neke elemente koji se kristaliziraju u kubičnoj rešetki s prostornim centrima. Te vrijednosti su provjerene rendgenskim snimkama:
Litij Natrij Kalij Volfram Alfa-željezo Molna masa M 6,94 22,997 39,096 184 55,84 Gustoća ρ 0,534 0,97 0,86 19,3 7,86 Razmak između atoma a (nm) 35,1 43,0 53,3 31,59 28,61
Vidi se odmah da kubična rešetka s prostornim centrima ne prestavlja najgušći oblik rešetke. Gušća je kubična rešetka s plošnim centrima. Tu otpadaju četiri čestice na svaku elementarnu ćeliju. Jedna čestica određuje početni čvor ćelije, a tri čestice leže u centrima stranica koje polaze od te točke. Prema tome, između volumena ćelije a3 i volumena V koji otpada na česticu postoji kod kubične rešetke s plošnim centrima relacija:
Brid ćelije dan je sada izrazom:
Prema toj jednadžbi izračunati su razmaci između atoma za neke elemente i korigirani rendgenskim zrakama:
Aluminij Bakar Srebro Platina Olovo Molna masa M 26,97 63,57 107,88 195,23 207,22 Gustoća ρ 2,72 8,93 10,5 21,4 11,34 Razmak između atoma a (nm) 40,41 36,08 40,78 39,16 49,39
Razmaci između čestica kristala veličine su istog reda kao i molekularni promjeri. Približnu sliku kristala možemo dobiti ako atome ili molekule predočimo kao kugle koje su naslagane jedna do druge. Već prema tome kako slažemo kugle jednu do druge dobivamo različite tipove elementarnih ćelija.
Kristalna rešetka vrlo je čvrsta tvorevina. Ona se teško razara mehaničkim silama. Oko svojih položaja ravnoteže koji se podudaraju sa čvorovima rešetke mogu se atomi samo malo pomicati. Kristalnu rešetku možemo razoriti tako da čvrsto tijelo ugrijemo do temperature tališta. Tada temperaturna titranja atoma prevladavaju kohezione sile, i kristalna struktura iščezava. Teorija sila koje drže rešetku izlazi iz okvira klasične fizike i pripada modernoj valnoj mehanici (L. de Broglie, Heisenberg, E. Schrödinger). [2]
Bravaisove ili translacijske rešetke
| Kristalni sustavi | |||||||||||||||||||
| Redni broj | Kristalni sustav | Tip rešetke | Elementarna ćelija | ||||||||||||||||
| Međusobni odnos bridova i kutova | Bridovi i kutovi koji su specifični | Broj rešetki | Simetrija rešetke | Primitivna | Bazno centrirana | Volumno centrirana | Plošno centrirana | ||||||||||||
| 1 | Triklinska | a≠b≠c α≠β≠γ | a,b,c, α,β,γ | 1 | - | - | - | ||||||||||||
| 2 | Monoklinska | a≠b≠c α=γ=90°≠β | a,b,c, β | 2 | - | - | |||||||||||||
| 3 | Rompska | a≠b≠c α=β=γ=90° | a,b,c | 4 | |||||||||||||||
| 4 | Trigonska | a=b=c α=β=γ<120°≠90° | a α | 1 | - | - | - | ||||||||||||
| 5 | Tetragonska | a=b≠c α=β=γ=90° | a, c | 2 | - | - | |||||||||||||
| 6 | Heksagonska | a=b≠c α=β=90° γ=120° | a,c | 1 | - | - | - | ||||||||||||
| 7 | Kubna | a=b=c α=β=γ=90° | a | 3 | - | ||||||||||||||
Izvori
- ↑ Bravais, Auguste, [1] "Hrvatska enciklopedija", Leksikografski zavod Miroslav Krleža, www.enciklopedija.hr, 2019.
- ↑ Ivan Supek: "Nova fizika", Školska knjiga Zagreb, 1966.











![{\displaystyle a={\sqrt[{3}]{2\cdot V}}={\sqrt[{3}]{\frac {2\cdot M}{L\cdot \rho }}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/eba3f5495c866c9803229f5ed6147d322115c7a5)

![{\displaystyle a={\sqrt[{3}]{4\cdot V}}={\sqrt[{3}]{\frac {4\cdot M}{L\cdot \rho }}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c5b8729e182d7afad292083e111e985196dfdc3a)






