Vibracijska spektroskopija

Apsorpcijski spektar klorovodika.

Molekularne vibracije kod klorovodika HCl.

Dipolna molekula vode: μ = 6,14·10^-30 Cm.

Datoteka:Molekularne rotacije 1.jpg

Molekularne rotacije ugljikova dioksida CO₂.

Razine energije i položaji spektralnih linija izračunati u aproksimaciji krutog rotora (rotator).

Dio rotacijskog spektra trifluoroiodimetana, CF₃I. Svaki rotacijski prijelaz označen je kvantnim brojevima J, konačnog i početnog stanja, a uvelike je podijeljen djelovanjem spajanja nuklearnog četveropola sa jezgrom ¹²⁷I (jod-127).

Apsorpcijski spektar klorovodika HCl u infracrvenom području.

Apsorpcijski spektar metana CH₄ u infracrvenom području.

Dijagram energetskih razina koji opisuju neke prijelaze koji su uključeni u infracrveni rotacijskotitrajni spektar linearne molekule: R grana (l' = l - 1), P grana (l' = l + 1), Q grana (l' = l).

Toplinske vibracije dijelova bjelančevine: amplituda vibracija raste s temperaturom.

Spektar plamena alkohola.

Vibracijska spektroskopija je grana spektroskopije koja proučava spektre, koji su uzrokovani vibracijama molekula. To obuhvaća infracrvenu spektroskopiju i Ramanovu spektroskopiju.

Vibracijski spektar je dio spektra elektromagnetskog zračenja, većinom u infracrvenom području, valne duljine od 0,1 μm do 3 mm, koji potječe od vibracija atoma i elektrona unutar molekule ili kristalne rešetke. Primjenjuje se za određivanje duljine i jakosti veza između atoma u molekuli, određivanje energije disocijacije molekula, te za kvalitativnu i kvantitativnu kemijsku analizu u krutim, tekućim i plinovitim uzorcima. Poznavanje vibracijskih i rotacijskih spektara neke molekule omogućava njezino prepoznavanje u industrijskim procesima i okolišu.

Vibracije molekula

Podrobniji članak o temi: Molekularne vibracije

Molekularne vibracije su titranja atoma oko ravnotežnih položaja u molekulama, odnosno gibanja kod kojih dolazi do promjene relativnih položaja atoma u molekuli. Dvoatomne molekule mogu vibrirati samo na jedan način (istezanjem i stiskanjem). Troatomne nelinearne molekule, na primjer voda H₂O, silicijev dioksid SO₂, ozon O₃, mogu vibrirati na tri načina, a linearne troatomne molekule, na primjer cijanovodična kiselina HCN i ugljikov dioksid CO₂, mogu vibrirati na četiri načina. Općenito, nelinearna molekula koja sadrži N atoma može vibrirati na 3 ∙ N – 6 načina, a linearna molekula koja sadrži N atoma na 3 ∙ N – 5 načina. Energijske su razine molekularnih vibracija točno određene, a prijelaz između razina može se dogoditi jedino ako molekula emitira ili apsorbira foton energije jednak razlici dviju vibracijskih energijskih razina.

Sve molekule vibriraju. Molekulske vibracije, za razliku od vibracija makroskopskih tijela, su kvantizirane. Molekula može vibrirati točno određenim amplitudama, koje odgovaraju vibracijskim energijskim razinama. Spektroskopski prijelaz se može dogoditi jedino ako je energija apsorbiranog ili emitiranog fotona jednaka razlici dviju vibracijskih energijskih razina (Bohrov uvjet), odnosno ako je razlika energija raspršenog i dolazećeg fotona jednaka razlici energijskih razina.

Ukoliko vibracija molekule uzrokuje promjenu dipolnog momenta molekule, vibracija će se sprezati s elektromagnetskim zračenjem i doći će do apsorpcije ili emisije zračenja. Takva vibracija će biti aktivna u infracrvenom spektru. Vibracija će biti aktivna u Ramanovom spektru ako vibracija uzrokuje promjenu polarizabilnosti molekule. Elektromagnetsko zračenje se može sprezati i s kvadrupolnim ili magnetskim momentom, ali ta sprega je vrlo slaba, pa je takve vibracije izuzetno teško proučavati.

Spektri molekula

Nuklearna mehanika ima svoj početak u Bohrovim razmatranjima o rotatoru. Rotatorom zovemo fizikalno tijelo ili česticu koja se vrti oko čvrstog centra. Tipičan primjer rotatora prestavljaju dvoatomne molekule kao fluorovodik HF, klorovodik HCl, HJ i tako dalje. Kod tih molekula laki se vodikov atom okreće oko drugog znatno težeg atoma. Energija molekule, sadržana u vrtnji, u tom je slučaju direktno dana kinetičkom energijom vodikova atoma. Kod vrtnje je zgodno uvesti moment impulsa. Zamislimo da kamen vrtimo oko ruke. Tad najedanput počnimo polagano vuči konop i skraćivati polumjer staze kamena. Pri tom se brzina okretanja povećava tako da umnožak polumjera i brzine ostaje stalan (konstantan). Konstantni umnožak m∙v∙r zove se momentom impulsa i on u neku ruku mjeri jačinu okretanja. Kinetičku energiju čestice, koja se vrti u kružnici s polumjerom r možemo prema tome pisati u obliku:

[math]\displaystyle{ E = \frac{1}{2 \cdot m \cdot r^2} \cdot (r \cdot m \cdot v)^2 = \frac{1}{2 \cdot J} \cdot p_{\phi}^2 }[/math]

Moment impulsa ili impuls vrtnje označili smo sa p_Φ, a moment tromosti m∙r² sa J. Impuls vrtnje stoji u istom odnosu s kutom Φ, što ga opisuje polumjer vrtnje, kao što stoji kod pravocrtnog kretanja (translacije) obični impuls m∙v s običnom koordinatom x.

Promatrajući spektre molekula, N. Bjerrum je prvi došao na pomisao da u vrtnjama molekula mora vladati diskontinuitet. Kako sam spominje, dobio je N. Bohr ovom idejom moćan poticaj. Bohr je sasvim općenito pretpostavio da moment impulsa čestice, koja se vrti, mora biti cijeli broj osnovne veličine h/2π:

[math]\displaystyle{ M = r \cdot m \cdot v = l \cdot \frac{h}{2 \cdot \pi} }[/math]

gdje je: l - neki cijeli broj.

Energija molekule E s kvantiziranim momentom impulsa M jednaka je:

[math]\displaystyle{ E = \frac{1}{2 \cdot J} \cdot M^2 = \frac{h^2}{8 \cdot \pi^2 \cdot J} \cdot l^2 }[/math]

U analogiji s klasičnim frekvencijama, Bohr je zaključio da se impuls vrtnje može promijeniti samo za veličinu h/2J. Molekula koja iz stanja l prelazi u stanje l - 1 emitira spektralnu liniju frekvencije:

[math]\displaystyle{ \nu = \frac{E_l - E_{l-1}}{h} = \frac{h}{4 \cdot \pi^2 \cdot J} \cdot (l - \frac{1}{2}) }[/math]

Ovaj izraz malo ćemo popraviti. Potpuno slaganje s iskustvom postiže se kad se ispusti dodatni član 1/2. Prema tome, frekvencije emitiranih linija iznose:

[math]\displaystyle{ \nu = \frac{h}{4 \cdot \pi^2 \cdot J} \cdot l }[/math]

Rotacijski spektri molekula dani su nizom linija koje imaju među sobom jednaki razmak. Razmak između spektralnih linija iznosi:

[math]\displaystyle{ \Delta \nu = \frac{h}{4 \cdot \pi^2 \cdot J} }[/math]

Pokusima se takvi ekvidistantni (s jednakim razmacima) spektri opažaju duboko u infracrvenom području. Za svaku vrst molekula svojstven je razmak između linija. Kod tako jednostavnih molekula, kao što su HCl, HF ili HJ, možemo odmah proračunati moment tromosti J. On je jednak umnošku mase vodikova atoma s kvadratom udaljenosti između težišta obaju atoma. Znamo da je masa vodikova atoma jednaka 1,67∙10^-27 kg, a iz kinetičke teorije materije izlazi da je razmak atoma u molekuli HCl jednak 1,3∙10^-10 m. Prema tome dobivamo da je svojstven razmak između rotacijskih linija HCl jednak 6∙10¹¹. Ova vrijednost vrlo dobro se slaže s opažanjima.

Po iskustvu samo one dvoatomne molekule, koje imaju električki dipol, emitiraju rotacioni spektar. Simetrične molekule kao H2 i N2, gdje težište negativnog naboja pada zajedno s težištem pozitivnog, nemaju rotacionog spektra. Električki dipol predstavlja na primjer molekula HCl, pa shematski uzeti da se vodikov atom vrti oko čvrstog klorova atoma.

Prema kinetičkoj teoriji materije, vrtnje molekula pobuđene su temperaturnim gibanjem. Na osnovu računa vjerojatnosti sasvim smo općenito zaključili da na svaki stupanj slobode otpada energija 1/2∙k∙T. Budući da se molekula može vrtjeti oko 3 glavne osi, otpada na rotaciju energija 3/2∙k∙T. S ovim teorijskim rezultatom dobili smo ispravni specifični toplinski kapacitet plinova, osim u slučaju kad se plin sastoji od dvoatomnih molekula. Tu razliku (diskrepanciju) možemo sada objasniti. Iz gornje jednadžbe proizlazi da su energetski nivoi to viši, što je manji moment tromosti. Za glavnu os, koja prolazi kroz težišta obaju atoma, taj moment inercije je izvanredno malen. Prvi energetski nivo leži tu već vrlo visoko. Očito je, dakle, da vrtnja oko te osi uopće ne može biti pobuđena. Pri proračunu prosječne rotacijske energije dvoatomnih molekula moramo uzeti samo 2 stupnja slobode.

Prosječna rotacijska energija dvoatomnih molekula iznosi k∙T. Boltzmannova konstanta k jednaka je 1,37∙10-23 J/K, pa prosječna rotacijska energija molekula na sobnoj temperaturi iznosi oko 4∙10-21 J. Izjednačimo li to s gornjom jednadžbom, vidimo da se molekule HCl na sobnoj temperaturi moraju nalaziti oko stanja s kvantnim brojem l = 5. Linije u emisijskom ili apsorpcijskom spektru klorovodika imaju među sobom razmak 6∙10^-11. Emisijska linija, koja nastaje prijelazom iz stanja l = 5 u stanje l = 4, ima frekvenciju 5 puta veću od tog razmaka, što daje za valnu duljinu λ = 0,1 mm. Ta i sve druge linije leže duboko u infracrvenom dijelu spektra.

Rotacijske spektre možemo zato opažati kod spojeva vodika s halogenim elementima fluorom, klorom, bromom i jodom, jer je moment tromosti njihovih molekula izvanredno malen. Kad bi oko osi okretanja bili znatno teži atomi, energetski nivoi ležali bi mnogo dublje i gušće, pa se rotacijska vrpca ne bi dala spektralnim aparatima rastaviti na linije. Vidljive vrpce osim kod HF, HCl, HBr i HJ, dobivamo i kod simetričnih molekula CH₄ i NH₃. Tu prolaze osi vrtnje kroz teški ugljikov ili dušikov atom, pa njihova masa ne pridonosi momentu tromosti. Zanimljiva su opažanja na molekuli vode. Da su tu dva vodikova atoma simetrično postavljena s jedne i druge strane kisikova atoma na istom pravcu, imali bismo iste rotacijske spektre kao i kod HCl. Međutim, to se ne opaža. Rotacijski spektri vode mogu se objasniti predodžbom da 3 atoma molekule čine trokut, što je u skladu i s mjerenjima električnog momenta molekule.

Rotacijskotitrajni spektri

Spektri molekula, koje smo dosad razmatrali, čisti su rotacijski spektri. Oni potječu od promjene energije vrtnje. No molekula nije kruti sistem, i njeni atomi mogu izvoditi titranja oko svojih položaja ravnoteže. Promjena titrajne energije mora se također mora se također odraziti u molekularnim spektrima. Iz iskustvenih podataka o specifičnim toplinskim kapacitetima plinova proizlazi da su titranja na normalnoj temperaturi tek neznatno pobuđena. Iskustvene vrijednosti specifičnih toplinskih kapaciteta plinova mogli smo ispravno izračunati uzevši u obzir samo energije vrtnje. Dok su kvantni brojevi vrtnje mnogobrojno zastupani, za kvantne brojeve titranja dolaze tek vrijednosti 0 ili 1. Označimo sa ν₀ frekvenciju titranja atoma u molekuli. Tad je po Planckovoj hipotezi energija titranja molekula jednaka n∙h∙ν₀. Ukupna energija molekula jednaka je sumi rotacijske i titrajne energije:

[math]\displaystyle{ E = \frac{h^2}{8 \cdot \pi^2 \cdot J} \cdot l^2 + n \cdot h \cdot \nu_0 }[/math]

Pri kvantnom skoku može molekula istovremeno promijeniti i energiju vrtnje i energiju titranja. Frekvencija emitirane spektralne linije jednaka je:

[math]\displaystyle{ \nu = \frac{h}{8 \cdot \pi^2 \cdot J} \cdot (l^2 - l'^2) + \nu_0 \cdot (n - n') }[/math]

Promatrajmo emisijske linije. Titrajne energije znatno nadmašuju rotacijske. Prema tome, pri emisiji može se titrajna energija samo umanjiti. Stavljamo, dakle, n - n' = 1. No rotacijska energija mogla se pri tom umanjiti ili povećati. Imamo dva slučaja: l' = l - 1 i l' = l + 1. Prema tome imamo i dvije grupe frekvencija:

[math]\displaystyle{ \nu = \nu_0 + \frac{h}{4 \cdot \pi^2 \cdot J} \cdot l }[/math]

[math]\displaystyle{ \nu = \nu_0 - \frac{h}{4 \cdot \pi^2 \cdot J} \cdot (l + 1) }[/math]

Aditivni član 1/2 opet smo ispustili.

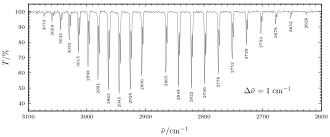
Težište linija dano je frekvencijom titranja. Lijevo i desno imamo dvije grane, od koji jedna odgovara povećanju rotacijskog kvantnog broja, a druga umanjenju. Takvi rotacijski titrajni spektri mjereni su s velikom točnošću. Na slici (apsorpcijski spektar klorovodika HCl u infracrvenom području) vidimo pozitivnu i negativnu stranu rotacijskotitrajnog spektra. Iz usporedbe s čisto rotacijskim spektrom molekule vidi se za koju su frekvenciju ν₀ povećane frekvencije rotacijskotitrajnog spektra.

Prema prethodnim jednadžbama bio bi spektar molekula strogo s jednakim razmacima (ekvidistantan). Međutim, ako se pogledaju slike nekim spektara molekula vidi se da to nije savršeno. Razmak između linija smanjuje se prema manjim valnim duljinama ili višim frekvencijama. To je jasno ako pomislimo da titranje atoma izaziva promjenu momenata tromosti. Samo dok se rotacija i titranje promatraju kao potpuno nezavisni dobivaju se strogo linije s jednakim razmacima (ekvidistantne).

S promjenom rotacijske i titrajne energije molekula može se kombinirati i skok elektrona. Promjena elektronske energije znatno je veća i ona može uzrokovati da se molekularna vrpca pojavi u vidljivom području spektra.

Skok elektrona izaziva znatnu promjenu molekule. Zbog toga će se znatno promijeniti moment tromosti i frekvencija titranja. Cjelokupna promjena energije molekule nastaje promjenom elektronske energije E₂, energije titranja E_t i rotacijske energije molekule:

[math]\displaystyle{ \Delta E = E_e - E'_e + E_t - E'_t + \frac{h^2 \cdot l^2}{8 \cdot \pi^2 \cdot J} - \frac{h^2 \cdot l'^2}{8 \cdot \pi^2 \cdot J'} }[/math]

Opet će kvantni broj l poprimiti vrlo različite vrijednosti. Pri tom treba pomisliti da i elektron ima moment impulsa, što omogućuje prijelaz i bez promjene rotacije. Prema tome su za promjenu rotacijskog kvantnog broja moguća tri slučaja:

l' = l - 1 → R grana

l' = l + 1 → P grana

l' = l → Q grana

Već prema ta 3 slučaja dobivamo tri grupe frekvencija koje ovise kvadratično o kvantnom broju l. Na slici vide se tri grane. Kao apscisa nanesena je frekvencija, a kao ordinata l. U tom dijagramu pojavljuje se tri grane kao tri parabole. Iz grafičkog prikaza može se odmah razabrati spektar. Linije se zgušćuju prema kraju. Ovo zgušćivanje, koje je tipično za sve vrpce u vidljivom dijelu spektra, izazvano je promjenom momenta tromosti molekule.

Kad promatramo molekularne spektre u vidljivom području, tad opažamo niz vrpca. Razmaci između pojedinih vrpca određeni su promjenom titrajne energije. Struktura vrpce, to jest broj linija i njihovo zgušćivanje prema jednom kraju, određeno je promjenom rotacijske energije. Da se ovaj niz vrpca pojavio u vidljivom području, uzrok je kvantni skok nekog elektrona. To je sumarna slika vrpčastog spektra, dobivena na osnovu kvantne teorije.

Opća načela

Molekule se, kao što je gore objašnjeno, ne ponašaju kao makroskopski objekti. Energijske razine molekule, moguće je dobiti kao rješenja Schrödingerove jednadžbe, ako se u jednadžbi zada odgovarajući potencijal. U općem slučaju, potencijal se može prikazati kao Taylorov red:

[math]\displaystyle{ U(r)=U(r_0)+\left(\frac{\partial U}{\partial r}\right)_{r0}\left(r-r_0\right)+\frac{1}{2}\left(\frac{\partial^2U}{\partial r^2}\right)_{r_0}(r-r_0)^2+\frac{1}{6}\left(\frac{\partial^3 U}{\partial r^3}\right)_{r_0}(r-r_0)^3+... }[/math]

Schrödingerova jednadžba s ovako zadanim potencijalom se ne može analitički riješiti, pa se često pribjegava aproksimacijama. Prvi član: [math]\displaystyle{ U(r_0) }[/math] opisuje nultočku energije i može se staviti na nulu. Drugi član: [math]\displaystyle{ \left(\frac{\partial U}{\partial r}\right)_{r0}\left(r-r_0\right) }[/math] je gradijent potencijala. S obzirom da molekula vibrira oko ravnotežnog položaja, drugi član mora biti jednak nuli (u ravnoteži, molekula je u minimumu potencijala, pa je gradijent jednak nuli). Prva aproksimacija je da se u jednadžbi odbace svi osim trećeg člana u razvoju. Ova aproksimacija se naziva aproksimacija harmoničkog oscilatora, jer dani potencijal opisuje harmonički oscilator.

Harmonički oscilator

Derivacija potencijala u prethodnoj jednadžbi je konstanta koja ovisi o čvrstoći sustava koji vibrira. Potencijal u kojem se gibaju mase (atomi) može se jednostavno zapisati:

[math]\displaystyle{ U(x)=k(r-r_0)^2 }[/math]

Rješavanjem jednadžbi gibanja za dani potencijal, dobiva se klasična frekvencija:

[math]\displaystyle{ \omega_e=\frac{1}{2\pi}\sqrt{\frac{k}{\mu}} }[/math]

gdje je [math]\displaystyle{ \mu }[/math] reducirana masa atoma koji titraju. Kako je gore rečeno, molekule se ne ponašaju kao makroskopski objekti, pa je za opis vibracijskog gibanja potrebno primijeniti kvantnu mehaniku. Kao rješenje Schrödingerove jednadžbe dobivaju se diskretne energijske razine; vibracijski term je:

[math]\displaystyle{ G(v)=\omega_e(v+\frac{1}{2}) }[/math]

gdje je [math]\displaystyle{ v }[/math] vibracijski kvantni broj. Vibracijski kvantni broj može biti bilo koji pozitivni cijeli broj, uključujući i nulu: [math]\displaystyle{ v=0, 1, 2, 3, ... }[/math]. Iz prethodne jednadžbe je primjetljivo da je u nultoj vibracijskoj razini, energija različita od nule! Čak i u najnižem vibracijskom stanju, molekula vibrira i ne može izgubiti tu energiju vibracije. Ta energija se naziva energija nulte točke (eng. zero point energy):

[math]\displaystyle{ E_{ZPE}=\frac{hc\omega_e}{2} }[/math]

Izborno pravilo za vibracijski prijelaz harmoničkog oscilatora je [math]\displaystyle{ \Delta v=\pm1 }[/math]. Iz toga se može izračunati energija fotona:

[math]\displaystyle{ E = \Delta G=hc\omega_e }[/math]

Kako je razlika između svih susjednih energijskih razina jednaka za sve energijske razine, jedan harmonički oscilator može dati samo jednu liniju u spektru.

Anharmonički oscilator

Molekule nisu harmonički oscilatori. Philip M. Morse je dao puno bolji potencijal koji opisuje gibanja atoma unutar molekule. Morseov potencijal vrlo dobro opisuje produljivanje i skraćivanje veze između dva atoma:

[math]\displaystyle{ U(x)=D_e[1-e^{-\beta(x-x_0)}]^2 }[/math].

Schrödingerova jednadžba jednadžba za gibanje u Morseovom potencijalu se može egzaktno riješiti; kao rezultat se dobivaju termovi za anharmonički oscilator:

[math]\displaystyle{ G(v)=\omega_e\left(v+\frac{1}{2}\right)-\omega_ex_e\left(v+\frac{1}{2}\right)^2 }[/math]

Usporedba Morseovog i harmoničkog oscilatora.

Izborna pravila za Morseov oscilator dopuštaju i druge prijelaze: [math]\displaystyle{ \Delta v = 0, \pm 1, \pm 2, ... }[/math]. Prijelazi s većim [math]\displaystyle{ \Delta v }[/math] su manje vjerojatni i daju spektralne linije (vrpce) manjeg intenziteta. Prijelazi [math]\displaystyle{ \Delta v= \pm 2 }[/math], [math]\displaystyle{ \Delta v = \pm 3 }[/math], ... se nazivaju overtonovi. Prijelazi 2<-1, 3<-2, ... se ne poklapaju s prijelazom 1<-0, kao kod harmoničkog oscilatora, već se, u spektru vide kao odvojene linije. Ovi prijelazi se nazivaju vrući prijelazi, jer intenzitet njihovih spektralnih linija (vrpci) jako ovisi o temperaturi. Razlike susjednih energijskih razina se smanjuju, kako se vibracijski kvantni broj [math]\displaystyle{ v }[/math] povećava, sve dok ta razlika ne postane nula. Ta energijska razina je i zadnja jer se sustav s energijom većom od najviše energijske razine raspada. Morseov oscilator može opisati disocijaciju molekula! Vrijednost [math]\displaystyle{ D_e }[/math] je zapravo disocijacijska energija anharmoničkog oscilatora iz ishodišta energije (zanemarujući energiju nulte točke). Maksimalna vibracijska energija Morseovog oscilatora se može izračnati po formuli:

[math]\displaystyle{ v_{max}=\frac{1}{2x_e}-1 }[/math]

Razlika u energijama između harmoničkog oscilatora i Morseovog oscilatora je mala, kada su i vibracijski kvantni brojevi mali. Kod velikih vibracijskih kvantnih brojeva, harmonički oscilator jako griješi. Kako se molekule pri sobnim temperaturama, nalaze u najnižim vibracijskim stanjima, harmonički oscilator je opravdana aproksimacija i često se koristi.

Dunhamov oscilator

Dunham je uspio numerički riješiti Schrödingerovu jednadžbu za općeniti potencijal i povezati rezultate s rezultatima rješenja Morseovog potencijala. Term Dunhamovog oscilatora je:

[math]\displaystyle{ G(v) = \omega_e \left( v + \frac{1}{2} \right) - \omega_e x_e \left( v + \frac{1}{2} \right) ^2 + \omega_e y_e \left( v + \frac{1}{2} \right) ^3 - \omega_e z_e \left( v + \frac{1}{2} \right) ^4 + ... }[/math]

Dunhamov potencijal se koristi pri analizi spektra; položaji spektralnih linija se određuju metodom najmanjih kvadrata, a u jednadžbu se uzima onoliko članova, koliko daje željenu preciznost.

Rotacijska struktura

Svaka molekula, pored vibracijskih stupnjeva slobode, ima i rotacijske stupnjeve slobode, ako se ne nalazi u okolini koja će spriječiti rotaciju (molekule koje tvore kristalnu ili amorfnu strukturu). Molekulske rotacije sadrže oko stotinu puta manje energije nego vibracije. To znači da jedno vibracijsko stanje sadrži mnogo rotacijskih stanja. Srednja vrijednost atomskih udaljenosti harmoničkog oscilatora su jednake za sve vibracijske razine. To znači da će i rotacijske konstante tih vibracijskih razina biti jednake. Morseov potencijal nije simetričan kao i harmonički (vidi sliku), pa su i srednje vrijednosti atomskih udaljenosti različite za različite vibracijske razine. Srednje vrijednosti atomskih razmaka se povećavaju s povećavanjem vibracijskog kvantnog broja. To znači da će rotacijske konstante biti različite za različita vibracijska stanja. To je i glavni razlog sprezanja vibracija i rotacija. Termovi rotiajućeg Morseovog oscilatora su:

[math]\displaystyle{ G(v,J) = \omega_e \left( v + \frac{1}{2} \right) - \omega_e x_e \left(v + \frac{1}{2} \right)^2 + B_e J(J + 1) - D_e [J(J+1)]^2 - \alpha_e \left( v + \frac{1}{2} \right) J(J+1) + ... }[/math]

[math]\displaystyle{ B_e }[/math] i [math]\displaystyle{ D_e }[/math] su rotacijske konstante, a [math]\displaystyle{ \alpha_e }[/math] je konstanta sprezanja rotacije i vibracije.

Spektar vibracijskog prijelaza između najnižih vibracijskih stanja ugljikovog monoksida.

Dunham je napravio općenitiji izraz za rotirajući oscilator:

[math]\displaystyle{ G(v,J)=\sum_{j,k} Y_{j,k} \left ( v + \frac{1}{2} \right )^j [J(J+1)]^k }[/math]

Konstante [math]\displaystyle{ Y_{j,k} }[/math] se mogu povezati s konstantama u prethodnoj jednadžbi.

[math]\displaystyle{ Y_{10} = \omega_e }[/math]

[math]\displaystyle{ Y_{20} = -\omega_e x_e }[/math]

[math]\displaystyle{ Y_{30} = \omega_e y_e }[/math]

[math]\displaystyle{ Y_{40} = \omega_e z_e }[/math]

[math]\displaystyle{ Y_{01} = B_e }[/math]

[math]\displaystyle{ Y_{11}= \alpha_e }[/math]

[math]\displaystyle{ Y_{12} = \gamma_e }[/math]

[math]\displaystyle{ Y_{02} = -D_e }[/math]

[math]\displaystyle{ Y_{12} = -\beta_e }[/math]

[math]\displaystyle{ Y_{03} = H_e }[/math]

...

Vibracijski spektri koji pokazuju rotacijsku strukturu, zovu se vibronski spektri. Izborna pravila vibronskih spektara su: [math]\displaystyle{ \Delta v = \pm1, \pm2, \pm3 ... }[/math], [math]\displaystyle{ \Delta J = 0, \pm1 }[/math], za apsorpcijski ili emisijski spektar, te [math]\displaystyle{ \Delta v = \pm1, \pm2, \pm3 ... }[/math], [math]\displaystyle{ \Delta J = 0, \pm2 }[/math] za Ramanov prijelaz. Vibracijski prijelaz se sastoji od niza prijelaza među rotacijskim stanjima vibracijskog stanja koje tvore vibronske linije. Niz vibronskih linija čini vrpcu. Zbog izbornih pravila, vibronske vrpce su podjeljene na dvije ili tri grane. Grane vrpce se označavaju velikim latiničnim slovima: O za [math]\displaystyle{ \Delta J = -2 }[/math], P za [math]\displaystyle{ \Delta J = -1 }[/math], Q za [math]\displaystyle{ \Delta J = 0 }[/math], R za [math]\displaystyle{ \Delta J = +1 }[/math] i S za [math]\displaystyle{ \Delta J = +2 }[/math]. U apsorpcijskim/emisijskim spektrima, prosutne su P i R, a ponekad i Q grane, a u Ramanskim spektrima O i S, a ponekad i Q grana.