Elektrostatika

Elektromagnetizam

Elektricitet • Magnetizam Elektrostatika Električni naboj • Coulombov zakon • Električno polje • Električni tok • Gaussov zakon • Električni potencijal • Elektrostatska indukcija • Električni dipolni moment • Gustoća polarizacije Magnetostatika Ampèreov zakon • Električna struja • Magnetsko polje • Magnetizacija • Magnetski tok • Biot–Savartov zakon • Magnetski dipolni moment • Gaussov zakon za magnetizam Elektrodinamika Zrakoprazan prostor • Lorentzov zakon • ems • Elektromagnetska indukcija • Faradayev zakon • Lenzov zakon • Struja pomaka • Maxwellove jednadžbe • EM polje • Elektromagnetsko zračenje • Liénard-Wiechertov potencijal • Maxwellov tenzor • Vrtložne struje Električna mreža Električna vodljivost • Električni otpor • Električni kapacitet • Električni induktivitet • Impedancija • Rezonantne šupljine • Vodiči valova Kovarijantna formulacija Elektromagnetski tenzor • EM Stres-energijski tenzor • Četvero-struja • Elektromagnetski četvero-potencijal Znanstvenici Ampère • Coulomb • Faraday • Gauss • Heaviside • Henry • Hertz • Lorentz • Maxwell • Tesla • Volta • Weber • Ørsted

Istoimeni električni naboji se djelovanjem elektrostatičke sile odbijaju, a naboji suprotnog predznaka privlače.

Papir privučen natrljanim CD-om.

Munje iznad mjesta Oradea u Rumunjskoj.

Prikaz električnog polja i ekvipotencijalnih ploha oko pozitivnog električnog naboja u prostoru.

Elektrostatsko polje (linije sa strelicama) obližnjeg pozitivnog naboja (+) uzrokuje odvajanje pokretnih elekričnih naboja u vodljivim predmeta zbog elektrostatske indukcije. Negativni naboji (plavi) se privlače i pomiču na površinu predmeta koji je okrenut prema vanjskom naboju. Pozitivni naboji (crveni) odbijaju se i pomiču na površinu okrenutu prema van. Ovi inducirani površinski naboji su točno prave veličine i oblika tako da njihovo suprotno električno polje poništava električno polje vanjskog naboja u unutrašnjosti metala. Stoga je elektrostatsko polje svuda unutar vodljivog predmeta nula, a elektrostatski potencijal je konstantan.

Prikaz električnog polja koje okružuje pozitivni (crveno) i negativni (plavo) električni naboj.

Način rada elektroskopa s kuglicom.

Dielektrična polarizacija kod dielektrika.

Elektrostatika je grana fizike koja se bavi istraživanjem električnih polja, sila i pojava nastalih među električnim nabojima koji miruju.

Povijest

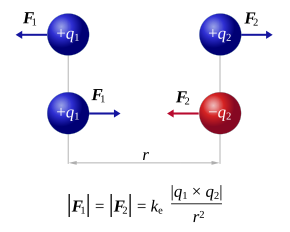
Prvi je Tales iz Mileta (600 pr. Kr.) pisao da jantar (grč. ἤλεϰτρον, ḗlektron), kada se tare, privlači sitne čestice tvari, a W. Gilbert otkrio je da i druge tvari, a ne samo jantar, imaju električno svojstvo. Pojavu električnoga odbijanja prvi je 1672. opazio Otto von Guericke, a 1663. konstruirao je prvi elektrostatički stroj na trenje. Razliku među vodičima i izolatorima otkrio je Stephen Gray. Francuski kemičar C. F. C. du Fay utvrdio je 1734. različitost električnog naboja nastalog trljanjem stakla od naboja nastalog trljanjem smole, a G. Ch. Lichtenberg nazvao je pozitivnim električni naboj nastao trljanjem stakla. Oko 1747. B. Franklin konstatirao je da se pri trenju stvaraju uvijek jednake količine pozitivnog i negativnog električnog naboja. Istraživanjem sila koje djeluju među električnim nabojima bavili su se H. Cavendish i J. Priestley, a zakon o ovisnosti privlačne ili odbojne sile o nabojima i udaljenosti među nabojima, a osnovi pokusa formulirao, C. A. de Coulomb, pa se po njemu mjerna jedinica električnog naboja naziva kulon (C). Prema Coulombovu zakonu sila F koja djeluje između dvaju točkastih električnih naboja q₁ i q₂ razmjerna je produktu obaju naboja, a obrnuto razmjerna kvadratu njihova razmaka r:

$F={\frac {1}{4\cdot \pi \cdot \varepsilon _{0}}}\cdot {\frac {q_{1}\cdot q_{2}}{r^{2}}}$

gdje je: ε₀ - dielektrična permitivnost vakuuma. Sila je najjača u vakuumu, a slabija u svim drugim sredstvima:

$F={\frac {1}{4\cdot \pi \cdot \varepsilon }}\cdot {\frac {q_{1}\cdot q_{2}}{r^{2}}}={\frac {1}{\varepsilon _{r}}}\cdot {\frac {1}{4\cdot \pi \cdot \varepsilon _{0}}}\cdot {\frac {q_{1}\cdot q_{2}}{r^{2}}}$

gdje je: ε_r - relativna dielektrična permitivnost nekog sredstva ili tvari, ε - dielektrična permitivnost (ili samo permitivnosti) tvari.

Sila F je vektor, pa je i jakost električnog polja E vektorska veličina, a kao smjer električnoga polja uzima se onaj smjer u kojem djeluju sile na pozitivni naboj. Električno polje može se opisati i skalarnim veličinama, potencijalima V. Električni naboji mogu pod utjecajem električnih sila obavljati mehanički rad, a to znači da u svakoj točki polja električni naboj q ima izvjesnu potencijalnu energiju (električni potencijal) s obzirom na neku referentnu točku u polju kojoj se pripisuje potencijal φ = 0. To je obično vrlo udaljena točka u polju ili Zemlja. Sve točke u polju koje imaju isti potencijal leže na ekvipotencijalnim plohama.

Za električni naboj q električni potencijal V neke točke na udaljenosti r iznosi:

$V={\frac {1}{4\cdot \pi \cdot \varepsilon _{0}}}\cdot {\frac {q}{r}}$

Budući da je razlika potencijala među dvjema točkama u elektrostatičkom polju jednaka električnom naponu među tim točkama, to će u elektrostatici, gdje naboji miruju, sve točke nekog vodiča biti na istom električnom potencijalu, jer bi inače zbog napona došlo do gibanja naboja. Iz odnosa U_ab = V_a – V_b proizlazi da se električni potencijal i električni napon mjere istom mjernom jedinicom volt (V), a jakost električnog polja mjeri se u voltima po metru (V/m).

Elektriziranje trenjem i dodirom

Već su stari Grci znali da kada se jantar protrlja svilom privlači mala tijela i odmah ih zatim odbija. Jantar se na grčkom jeziku zove elektron, pa je uzrok da jantar privlači tijela nazvan električnom silom. Tako je u znanost uveden izraz elektricitet. Protrljamo li štap od ebonita vunenom krpom, postaje električan i privlači male čestice tvari, ali ih odmah i odbija. Isto tako ako stakleni štap protrljamo suhim papirom ili amalgamiranom kožom, postaje električan. Dakle, trenjem tijela mogu postati električna. Kažemo da nose električni naboj, odnosno da su električno nabijena. Približimo li dva naelektrizirana staklena ili dva ebonitna štapa jedan drugome, vidjet ćemo da će se oni odbijati. Naprotiv, približimo li ebonitni štap staklenome, oni će se privlačiti. Prema tome, moramo razlikovati dvije vrste električnog naboja: pozitivan i negativan. Stakleni štap je pozitivno nabijen, a ebonitni negativno. Iz toga možemo zaključiti da se tijela istoimenog naboja odbijaju, a raznoimenoga privlače.

Međutim, tijela se mogu elektrizirati i dodirom. U to se možemo uvjeriti pomoću takozvanog električnog viska. Električni visak je kuglica od bazgine jezgre koja visi na staklenoj niti. Dotaknemo li takvu kuglicu naelektriziranim štapom, na nju će prijeći nešto elektriciteta pa će postati električna i odmah će se odbiti. Kažemo da je kuglica primila električni naboj. U to se možemo uvjeriti tako da kuglicu primaknemo papirićima: ona ih privlači. Prema tome, tijelo postaje električno ne samo trenjem nego i dodirom, s drugim električnim tijelom. Ako od dva jednaka električna viska nabijemo jednu kuglicu staklenim, a drugu ebonitnim štapom, kuglice će se privući, ali čim se dotaknu, one će se rastaviti i nakon toga neće više biti električne. Znači, raznoimeni elektriciteti iste množine odnosno istog električnog naboja međusobno se neutraliziranu, to jest poništavaju.

Coulombov zakon

Podrobniji članak o temi: Coulombov zakon

U povijesti znanosti o elektricitetu temeljni je bio zakon koji je našao 1785. C. A. de Coulomb o sili između električki nabijenih tijela. Coulombova sila općenito se potpuno podudara s Newtonovom gravitacijom, samo što u njoj mjesto mase dolaze električni naboji q, koji mogu biti i pozitivni i negativni:

$F={\frac {q_{1}\cdot q_{2}}{r^{2}}}$

Konstanta proporcionalnosti stavljena je ovdje 1, što znači određenu jedinicu električnog naboja. Pozitivni i negativni predznak naboja vodi računa o tome da se elektrizirana tijela mogu i odbijati, a ne samo privlačiti kao kod Newtonove gravitacije.

Coulombov zakon električnog privlačenja i odbijanja vrijedi samo dotle dok su veličine električnog naboja male, pa ih možemo smatrati matematičkim točkama. Općenito su sile između elektriziranih tijela različite od Coulombove sile. Ponovo se može naći jednostavan zakon ako je jedno električno tijelo vrlo malo prema drugom.

Električno polje

Podrobniji članak o temi: Električno polje

Promatrajmo djelovanje električne sile na malu električnu kuglicu u blizini velikog elektriziranog metala. Iz ubrzanja ili iz pritiska nabijene kuglice na elastičnu oprugu možemo precizno mjeriti silu velikog metalnog tijela na malu kuglicu. Pokusi su pokazali da je sila na malu kuglicu to veća što je veći njezin električni naboj. Povećamo li naboj čestice dva puta, to je i sila u svakoj točki oko velikog tijela dvaput veća. Sila na malu kuglicu sukladna (proporcionalna) je njezinu električnom naboju. Mjesto da mijenjamo električni naboj kuglice, možemo je postavljati u različite položaje oko metalnog tijela. U svakoj točki prostora ima sila na malu kuglicu općenito različit smjer i veličinu. Električna sila na malu kuglicu ovisi dakle o jednom fizikalnom čimbeniku, koji je stvoren prisutnošću velikoga elektriziranog metalnog tijela. Taj čimbenik zove se električno polje elektriziranog metalnog tijela, a obično se označuje slovom E. Silu na mali električni naboj možemo prema tome izraziti umnoškom dvaju nezavisnih čimbenika, električnog naboja i električnog polja:

$F=q\cdot E$

Električno polje u prostoru možemo mjeriti tako da određene pojedinačne naboje stavljamo u različite točke oko velikog elektriziranog tijela i mjerimo silu, kojom djeluje veliko tijelo na malo. Električno polje E dano je tada s omjerom između sile i naboja male kuglice.

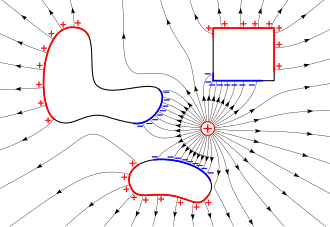
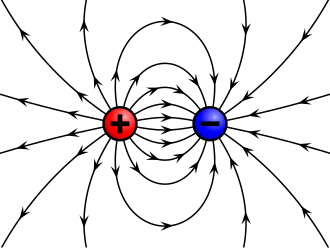
Sila na mali naboj q ima u svakoj točki općenito različitu veličinu i smjer, a tako mijenja i električno polje E. Električno polje ima uvijek smjer sile na mali električni naboj; smjer električnog polja poklapa se sa smjerom sile prouzrokovane na malu električnu kuglicu. Kad smo jedanput tako odredili električno polje u čitavom prostoru, možemo smjesta izračunati silu na bilo koji električni naboj. Ta sila dana je umnoškom povoljnog naboja i sada poznatoga električnog polja. Odavde se razabire praktična korist električkih polja, koja nam omogućuju da izračunamo sile na bilo kakve električne naboje. Grafički možemo električna polja oko električnih tijela prikazati vektorima ili strelicama, koja u svakoj točki prostora imaju duljinu jednaku veličini električnog polja, a smjer električnog polja.

Coulombovu električnu silu možemo također svesti na djelovanje električnih polja. Coulombovu silu na jedan naboj q₁ možemo prikazati kao umnožak toga naboja q₁ i električnog polja E, prouzročenog od drugog električnog naboja q₂. Električnom naboju q pripada na udaljenosti r električno polje E jednako:

$E={\frac {q}{r^{2}}}$

Električno polje je to veće, što je veći električni naboj q, a pada s kvadratom udaljenosti r. To je drugi oblik za isti Coulombov zakon. U Coulombovoj sili:

$F={\frac {q_{1}\cdot q_{2}}{r^{2}}}$

možemo uvijek jedan električni naboj odijeliti, pa silu prikazati kao umnožak toga odvojenog naboja i električnog polja, koje pripada drugom tijelu na udaljenosti r. Tada zamišljamo da je sila na taj naboj prouzrokovana djelovanjem električnog polja drugog naboja na taj odijeljeni naboj.

S obzirom na to da električno polje ima smjer radijvektora r, možemo ga pisati kao vektor:

${\vec {E}}={\frac {q}{r^{2}}}\cdot {\vec {r}}$

Električni potencijal

Podrobniji članak o temi: Električni potencijal

Jedna od najvažnijih električnih veličina je električni potencijal V. Na tu veličinu dolazimo ako promatramo rad koju vršimo micanjem jediničnog naboja u električnom polju. Označimo sa E_s projekciju vektora električnog polja na smjer malog puta ds. Općenito pri pomaku dr jedinični pozitivni naboj vrši mehanički rad jednak:

$W=E_{s}\cdot \mathrm {d} s$

Rad što ga vršimo na putu od točke a do točke b jednak je zbroju preko svih malih putova:

$W=E_{s1}\cdot \mathrm {d} s_{1}+E_{s2}\cdot \mathrm {d} s_{2}+E_{s3}\cdot \mathrm {d} s_{3}+....$

što možemo pisati kao integral, u granici sve manjih puteva ds:

$\int _{a}^{b}{E_{s}\cdot \mathrm {d} s}=V_{b}-V_{a}$

Izvršeni mehanički rad jednak je promjeni električnog potencijala V. Prema tome nam potencijal V daje energiju jediničnog pozitivnog naboja u električnom polju. Iz gornje jednadžbe, kao i iz prijašnje, vidi se da je potencijal određen do na povoljnu aditivnu konstantu. U tim jednadžbama ne mijenja se ni električno polje ni rad ako potencijalu dodamo povoljnu konstantu, to jest ako prijeđemo od V na novu funkciju V + konstanta. Prirodno je da tu konstantu odaberemo tako da potencijal u beskonačnoj udaljenosti od naboja iščezava. Taj izbor smo izvršili pri postavljanju funkcije e/r. Sada možemo odrediti jedinicu potencijala.

Elektrostatska jedinica električnog napona je jedan volt, a to je onaj električni napon između dvije točke pri kojoj se mora izvršiti rad od 1 džula da se jedinica električnog naboja kulon prenese od jedne točke do druge duljine 1 metar.

Električno polje pomnoženo električnim nabojem jednako je sili.

Ako jedan električni naboj po zatvorenoj krivulji vratimo na ishodište, tad iščezava cjelokupni rad što smo ga izvršili pri micanju naboja. To izlazi da je rad između dviju točaka jednak razlici potencijala u tim točkama. Po zatvorenoj krivulji je, dakle:

$\oint {E_{s}\cdot \mathrm {d} s}=0$

$W=\int _{a}^{b}{E_{s}\cdot \mathrm {d} s}$

Taj mehanički rad jediničnog električnog naboja određuje električni napon između dvije točke ili razlike potencijalne energije.

Kad taj linijski integral ne bi bio jednak nuli, tad bismo iz polja crpili povoljno mnogo energije da naboj vučemo mnogo puta po krivulji. No elektrostatsko polje ne može biti takvim izvorom energije. Rad po zatvorenom putu mora iščezavati. To je osnovni zakon za elektrostatsko polje.

Dugo vremena su električna polja shvaćali samo kao matematičke konstrukcije, kojima se vrlo pregledno mogu prikazati sile u okolini električnih naboja. Realnim su se shvaćale samo sile i električni naboji.

Električna polja su u kasnijem razvoju zadobila sve veću vrijednost. Pomalo su ih počeli prikazivati pomoću različitih mehaničkih modela. Postavljanje takvih mehaničkih modela ima veliku prednost da se takva polja mogu ne samo izračunati, već i zornim slikama prikazati. Takve zorne slike omogućuju brzi pogled nad fizikalnim odnosima. Polja se lijepo mogu predočiti silnicama. Gustoća silnica daje jakost polja, a tangenta na silnice prikazuje u svakoj točki smjer električnog polja. M. Faraday je u nizu godina neumornih pokusa došao na izvrsnu ideju da takva električna polja shvati kao prave stvarne tvorevine. S Faradayem su električna polja prestala biti matematičke izmišljotine, ona su dobila duboko fizikalno značenje. Mi nemamo osjetila za električna polja, ali ta okolnost nije nimalo smetala Faradaya da ta polja promatra kao stvarna, kao što su stvarna vidljiva fizikalna tijela. Dokaze o opstanku takvih polja iznijeli su Faraday i J. C. Maxwell promatranjem pojava, kod kojih se naglo mijenjaju električni naboji i struje.