Biot–Savartov zakon

Elektromagnetizam

Elektricitet • Magnetizam Elektrostatika Električni naboj • Coulombov zakon • Električno polje • Električni tok • Gaussov zakon • Električni potencijal • Elektrostatska indukcija • Električni dipolni moment • Gustoća polarizacije Magnetostatika Ampèreov zakon • Električna struja • Magnetsko polje • Magnetizacija • Magnetski tok • Biot–Savartov zakon • Magnetski dipolni moment • Gaussov zakon za magnetizam Elektrodinamika Zrakoprazan prostor • Lorentzov zakon • ems • Elektromagnetska indukcija • Faradayev zakon • Lenzov zakon • Struja pomaka • Maxwellove jednadžbe • EM polje • Elektromagnetsko zračenje • Liénard-Wiechertov potencijal • Maxwellov tenzor • Vrtložne struje Električna mreža Električna vodljivost • Električni otpor • Električni kapacitet • Električni induktivitet • Impedancija • Rezonantne šupljine • Vodiči valova Kovarijantna formulacija Elektromagnetski tenzor • EM Stres-energijski tenzor • Četvero-struja • Elektromagnetski četvero-potencijal Znanstvenici Ampère • Coulomb • Faraday • Gauss • Heaviside • Henry • Hertz • Lorentz • Maxwell • Tesla • Volta • Weber • Ørsted

Magnetsko polje oko ravnog električnog vodiča.

Smjer jakosti magnetskoga polja može se odrediti prema pravilu desne ruke: ako ispruženi palac pokazuje smjer električne struje, tada su prsti savinuti u smjeru jakosti magnetskoga polja.

Amper (A) je jakost one stalne električne struje koja, tekući kroz dva ravna, paralelna i neizmjerno duga električna vodiča, zanemarivo malog kružnog presjeka u vakuumu, međusobno udaljena 1 metar (m), prouzrokuje između njih silu od 2 ∙ 10^-7 njutna po metru (N/m).

Ampèreov zakon je fizikalni zakon koji izražava činjenicu da magnetsko polje nastaje kao posljedica gibanja električnih naboja.

Najjednostavniji je elektromagnet električna zavojnica kroz koju može teći električna struja.

Magnetsko polje zatvorene električne struje.

Biot–Savartov zakon ili Laplaceov zakon je fizikalni zakon koji opisuje vezu između jakosti magnetskoga polja i stalne električne struje koja ga je prouzročila. Otkrili su ga J. Biot i F. Savart izvodeći su pokus (1820.) s dugim ravnim električnim vodičem kojim teče električna struja I između dvaju magnetskih štapova. Pokazali su da je jakost magnetskoga polja na udaljenosti R od vodiča razmjerna električnoj struji I, a obrnuto razmjerna toj udaljenosti, i da smjer jakosti magnetskoga polja ovisi o smjeru električne struje. P. Laplace poopćio je taj eksperimentalni rezultat u matematički vektorski zakon, koji daje iznos i smjer jakosti magnetskoga polja dH u bilo kojoj točki prostora na udaljenosti r od elementa električne struje I, što protječe vodičem proizvoljna oblika:

$\mathrm {d} {\boldsymbol {H}}={\frac {1}{4\cdot \pi \cdot R^{2}}}\cdot (I\cdot d{\boldsymbol {\ell }}\times {\frac {\mathbf {r'} }{|\mathbf {r'} |}})$

gdje je dl infinitezimalna duljina žice u smjeru električne struje. Može se izraziti i u obliku:

$\mathrm {d} {\boldsymbol {B}}={\frac {\mu _{0}}{4\cdot \pi \cdot R^{2}}}\cdot (I\cdot d{\boldsymbol {\ell }}\times {\frac {\mathbf {r'} }{|\mathbf {r'} |}})$

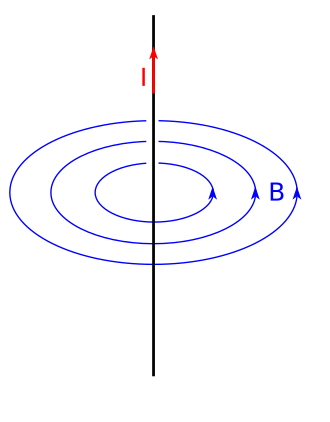
gdje je B - magnetska indukcija, a μ₀ - magnetska permeabilnost vakuuma. Smjer jakosti magnetskoga polja može se odrediti prema pravilu desne ruke: ako ispruženi palac pokazuje smjer električne struje, tada su prsti savinuti u smjeru jakosti magnetskoga polja.

Biot–Savartov zakon je temelj za magnetostatiku, gdje igra sličnu ulogu kao Coulombov zakon u elektrostatici. Kada se magnetostatika ne primjenjuje, Biot–Savartov zakon zamjenjuje se Jefimenkovim jednadžbama. Zakon vrijedi u magnetostatskoj aproksimaciji, a sukladan je i Ampèreovom kružnom zakonu i Gaussovom zakonu za magnetizam.

Električne struje (uzduž zatvorene krivulje / žice)

Biot–Savartov zakon koristi se za računanje rezultirajućeg magnetskog polja 'B' na položaju 'r' u 3D prostoru generiranom stalnom strujom "I" (na primjer zbog žice). Stalna (ili stacionarna) struja je kontinuirani protok električnog naboja koji se ne mijenja s vremenom, a električni naboj se ni u jednom trenutku ne akumulira niti iscrpljuje. Zakon je fizički primjer linijskog integrala, koji se procjenjuje na putu "C" u kojem prolazi struja (na primjer žica). Jednadžba u SI jedinicama je

$\mathbf {B} (\mathbf {r} )={\frac {\mu _{0}}{4\pi }}\int _{C}{\frac {Id{\boldsymbol {\ell }}\times \mathbf {r'} }{|\mathbf {r'} |^{3}}}$

gdje je $d{\boldsymbol {\ell }}$ vektor na putu $C$ čija je veličina duljina elementa diferencijal duljine žice u smjeru konvencionalne struje. $\mathbf {r'} =\mathbf {r} -{\boldsymbol {\ell }}$ je cijeli vektor pomaka elementa žice($d{\boldsymbol {\ell }}$) do točke u kojoj se izračunava polje ($\mathbf {r}$), a μ₀ je magnetska konstanta. Alternativno:

$\mathbf {B} (\mathbf {r} )={\frac {\mu _{0}}{4\pi }}\int _{C}{\frac {Id{\boldsymbol {\ell }}\times \mathbf {{\hat {r}}'} }{|\mathbf {r'} |^{2}}}$

gdje je $\mathbf {{\hat {r}}'}$ jedinični vektor vektora $\mathbf {r'}$. Simboli označeni podebljano označavaju vektorske veličine.

Integral je obično oko zatvorene krivulje, budući da stacionarne električne struje mogu teći samo oko zatvorenih staza kada su omeđene. Međutim, zakon vrijedi i za beskonačno dugu žicu (kako se koristi u definiciji SI jedinice električne struje - amper).

Za primjenu jednadžbe arbitražno se odabire točka ($\mathbf {r}$) u prostoru gdje se mora izračunati magnetsko polje. Držeći tu točku fiksiranom, izračunava se linijski integral preko puta električne struje kako bi pronašli ukupno magnetsko polje u toj točki. Primjena ovog zakona implicitno se oslanja na superpozicijski princip za magnetska polja, to jest na činjenicu da je magnetsko polje suma vektora polja stvorenog svakim infinitezimalnim dijelom žice pojedinačno.

Postoji i 2D verzija Biot-Savartove jednadžbe, koja se koristi kada su izvori nepromjenjivi u jednom smjeru. Općenito, struja ne treba protjecati samo u ravnini koja je okomita na nepromjenljivi smjer, a dana je pomoću $\mathbf {J}$ (gustoćom struje). Dobivena formula je:

$\mathbf {B} (\mathbf {r} )={\frac {\mu _{0}}{2\pi }}\int _{C}\ {\frac {(\mathbf {J} \,d\ell )\times \mathbf {r} '}{|\mathbf {r} '|}}={\frac {\mu _{0}}{2\pi }}\int _{C}\ (\mathbf {J} \,d\ell )\times \mathbf {{\hat {r}}'}$

Zakon se također koristi u aerodinamici, za izračunavanje brzine tijela na kojeg djeluju silnice vrtloga.

Električne struje i njihova magnetska polja

Elektricitet se može kretati, a to kretanje elektriciteta javlja se kao električna struja. Elektricitet se može kretati slobodno kroz prostor. Međutim, u povijesti klasične elektrodinamike bile su od najveće važnosti struje koje teku u metalnim žicama. Djelujemo li na metalne žice električnim naponom, u njima počinju teći struje. Električne su struje to jače, što je jače električno polje. Struju mjerimo količinom električnog naboja, koji prođe u jedinici vremena kroz presjek metalne žice. Prođe li u jednoj sekundi (s) električni naboj od 1 kulona (C) kroz presjek metalne žice, tada jakost struje iznosi 1 amper (A).

Električne struje bile su prvi fizikalni proces, koji je postavio most između magnetskih i električnih pojava. U početku bile su magnetske i električne pojave potpuno odijeljene; osim neke sličnosti u obliku zakona, nisu pokazivale nikakvu dublju vezu. Godine 1820. je H. C. Oersted otkrio, da se u okolini električnih struja nalazi magnetsko polje. Time je bila konačno nađena veza između magnetizma i elektriciteta. Električne struje proizvode magnetska polja oko sebe. Ta magnetska polja mogu se utvrditi djelovanjima na male magnete u blizini električnih struja. Poteče li električna struja kroz metalnu žicu, tada se počinju kretati i magneti u okolini struje. Teče li konstantna struja kroz metalnu žicu, i magnetsko polje ostaje konstantno. Iz djelovanja na magnet može se točno odrediti magnetsko polje, prouzrokovano strujom. Magnetska polja obavijaju električne struje poput prstenova. Smjer magnetskog polja leži u kružnicama koje koncentrično obavijaju struju. U svakoj točki iste koncentrične kružnice ima magnetsko polje istu vrijednost.

Magnetsko polje oko električnih struja prvi su točno proučili J. Biot i F. Savart iste godine, kada je i Oersted došao do svojeg otkrića. Pokusima se opaža, da je jakost magnetskog polja to veća što je veća struja. Teče li kroz metalnu žicu dvaput jača struja, to je i magnetsko polje dvaput jače. Nadalje, magnetsko polje ima manju vrijednost na većim udaljenostima od žice. Na dvaput većoj udaljenosti od žice ima magnetsko polje polovinu prvobitne veličine. Iskustveno je dakle potvrđeno da je veličina magnetskog polja razmjerna (proporcionalna) jakosti struje, a obrnuto razmjerna udaljenosti. Jakost električne struje označit ćemo sa J, a polumjer koncentrične kružnice sa r. Tada je magnetsko polje H na udaljenosti r jednako:

$H={\frac {2}{c}}\cdot {\frac {I}{r}}$

gdje je: c - konstanta razmjernosti. Iskustveno se dobiva da ta konstanta ima vrijednost jednaku 3∙10¹⁰. Iz gornje jednadžbe razabire se da konstanta proporcionalnosti c ima fizikalno značenje jedne brzine. Ona je dakle identična s brzinom svjetlosti. Konstanta c može se precizno odrediti iz Biot-Savartova zakona tako da mjerimo nezavisno magnetsko polje H, električnu struju J i udaljenost r. Takva točna mjerenja potpuno su utvrdila identičnost između elektromagnetske konstante i brzine svjetlosti. Ovo podudaranje potpuno je neočekivano postavilo zagonetnu vezu između dva u povijesti potpuno odijeljena područja, elektromagnetizma i optike.

Otkriće magnetskih polja u okolini električnih struja dobilo je veliku važnost u praksi. Električnim strujama mogu se proizvesti jaka magnetska polja, i tim poljima može se svijanjem žica dati povoljan oblik. Osim toga, jakost struje može se u metalnim žicama mijenjati, pa se tako mogu ujedno dobiti promjenjiva magnetska polja. To je velika prednost magnetskih polja struja pred magnetskim poljima prirodnih magneta. Mijenjanjem smjera struje u žici mijenja se i smjer magnetskog polja. Kada teče struja odozdo prema dolje, tada magnetsko polje ovija žicu zdesna nalijevo. U praksi mogu se proizvesti struje koje čas idu prema gore, čas prema dolje, a kako one izmjenično mijenjaju svoj smjer, tako isto mijenja svoj smjer i magnetsko polje. Takva magnetska polja koja periodički ovijaju žicu čas u smislu gibanja kazaljke na satu, a čas u suprotnom smjeru, od velike su važnosti u tehnici.

Postojanje magnetskih polja oko električnih struja navela je brzo na pomisao da su magneti možda rezultat električnih struja u molekulama ili atomima. Strogo matematički može se dokazati da je magnetsko polje oko kružne struje (na primjer električne zavojnice) jednako s magnetskim poljem koje okružuje mali magnet. Silnice magnetskog polja idu tada od jedne strane na drugu. Ta slika magnetskih silnica jednaka je sa silnicama koje okružuje magnet. Ova sličnost navela je Ampèrea na hipotezu da uopće nema magnetske tvari (supstancije), već da su magnetska polja samo popratna pojava električnih struja koje teku u atomima. Po toj Ampèreovoj hipotezi jasno je zašto se uvijek zajedno pojavljuje pozitivni i negativni pol; oni su dvije strane kruga na čijem rubu teče električna struja. Tom svojom teorijom Ampère je prethodio modernoj elektronskoj teoriji. Gibanje sitnih čestica elektriciteta, elektrona, u atomima prouzrokuje takve osnovne (elementarne) struje.

Treba da dokažemo jednakost (identičnost) između magnetskih polja zatvorenih struja i magnetskih dipola. Prije svega potrebni su nam neki opći stavci o magnetskim poljima. Vidjeli smo da magnetsko polje oko duge žice na udaljenosti r ima iznos:

$H={\frac {2\cdot I}{c\cdot r}}$

Silnice magnetskog polja su kružnice, koje ovijaju žicu. Izračunat ćemo mehanički rad što ga vrši magnetsko polje, kad pozitivni jedinični (zamišljeni) magnetski naboj obiđe kružnicu. Na jedinični naboj djeluje sila jednaka H. Uzmimo na kružnici linijski element ds. Smjer magnetskog polja poklapa se sa smjerom linijskog elementa. Na putu ds vrši magnetsko polje rad H∙ds. Mehanički rad po čitavoj kružnici jednak je umnošku iznosa polja H i opsega kružnice 2∙r∙π:

$H\cdot 2\cdot r\cdot \pi ={\frac {2\cdot I}{c\cdot r}}\cdot 2\cdot r\cdot \pi ={\frac {4\cdot \pi \cdot I}{c}}$

Rad što ga vrši magnetsko polje, kad jedinični naboj obiđe kružnicu oko žice, sukladan (proporcionalan) je jakosti struje. On ne ovisi o polumjeru kružnice. Taj rezultat vrijedi samo općenito. Uzmemo li oko struje bilo kakvu zatvrorenu krivulju, rad što ga magnetsko polje na tom putu vrši, proporcionalan je jakosti struje, koja teče unutar krivulje. Sa H∙s označit ćemo komponentu magnetskog polja na tangentu krivulje. H∙s∙ds je rad pri pomaku ds na krivulji. Integral po zatvorenoj krivulji jednak je:

$\int H_{s}\cdot d\mathbf {s} ={\frac {4\cdot \pi \cdot I}{c}}$

Da to dokažemo, potrebno je prije svega da uvidimo da je linijski integral magnetskog polja po zatvorenoj krivulji jednak nuli ako kroz krivulju ne teče električna struja:

$\int H_{s}\cdot d\mathbf {s} =0$

Kad to ne bi bilo tako, tad bi u statičkom magnetskom polju magnetski naboj dobivao po volji veliku energiju kad bi mnogo puta prolazio po takvoj stazi. To je očito nemoguće. Ako krivulja, naprotiv, obilazi oko električne struje, tada i statičko magnetsko polje može izvršiti rad. Potrebna energija dolazi tada od izvora električne struje. Zamislimo sada oko neke struje mali kružić, okomit na linijski element struje. Magnetsko polje u neposrednoj blizini struje podudara se s magnetskim poljem duge žice. Očito je za polje oko linijskog elementa bez važnosti da li dalje od tog mjesta ide žica ravno ili zakrivljeno. Prema tome je linijski integral magnetskog polja po maloj kružnici oko žice jednak 4∙π∙J/c. Uzmimo sad povoljnu krivulju oko žice. Obiđimo najprije tu krivulju, pa po nekom putu prijeđimo na mali kružić oko žice; obiđimo i njega, ali sad u protivnom smjeru, i vratimo se natrag do krivulje. Očito tako učinjen put ne zatvara struje, i prema tome linijski magnetskog polja iščezava. No, integral na dvostrukom putu po spojnici obiju krivulja ne poništava jer ide u suprotnom smjeru. Odatle izlazi da je linijski integral po povoljnoj krivulji jednak linijskom integralu po kružnici oko žice, uzetom u istom smjeru. Time je gornja integralna jednadžba dokazana. Ovaj zakon posljedica je Biot-Savartova zakona. No on se može neposredno pokusima utvrditi. Integral projekcije magnetskog polja po nekom putu znači razliku potencijala između početka i kraja puta:

$\int _{1}^{2}H_{s}\cdot d\mathbf {s} =V_{1}-V_{2}$

Ovaj magnetski napon između dvije točke može se direktno mjeriti. Ako se na zatvorenom putu vratimo na istu točku, tad je taj integral, kao i u elektrostatici, jednak nuli, izuzev da kroz površinu omeđenu krivuljom teku električne struje. U tom važnom slučaju je linijski integral magnetskog polja proporcionalan zbroju svih omeđenih struja.

Poslije ovog općeg razmatranja vratit ćemo se problemu koji smo postavili na početku: jednakosti (ekvivalentnosti) zatvorene struje s magnetom. Promatrati ćemo magnetsko polje oko električne struje koja teče u kružnoj žici. Sasvim blizu žice mora se magnetsko polje podudarati s magnetskim poljem oko duge žice. U blizini žice je sporedno da li ona dalje ide ravno ili se svija. Prvo što možemo zaključiti jest to magnetske silnice u blizini ovijaju žicu. Dalje iz simetrije moramo zaključiti da jedna magnetska silnica prolazi kroz os kružnice. Na taj način dobili smo već dobar uvid u magnetske silnice oko zatvorene kružne struje. Na prvi pogled se vidi da se njeno magnetsko polje podudara s poljem kratkog magneta koji bi imao oblik kola omeđenog električnom strujom. Naša je sada zadaća da proračunamo magnetski moment zamišljenog (fiktivnog) magneta, koji bi po svojem polju zamijenio električnu struju.

Promatramo prostor izvan magnetskog kola. Samo u tom prostoru mora se polje magneta podudarati s poljem zatvorene struje. Naravno, unutar magnetskog kola ide njegovo polje u obratnom smjeru od magnetskih silnica struje. U prostoru izvan kola očito je po zatvorenoj krivulji integral:

$\int H_{s}\cdot d\mathbf {s} =0$

To vrijedi za magnetsko polje zatvorene struje, jer u tom vanjskom prostoru ne teče nikakva struja. No za polje magneta vrijedi to i onda, ako zatvorena krivulja prolazi kroz električnu zavojnicu. U tome je bitna razlika između magnetostatičkih polja i magnetskih polja električnih struja. No mi upravo želimo postići slaganje samo između oba polja u okolnom prostoru zavojnice. Očito, ako se oba polja podudaraju, tada moraju imati istu potencijalnu razliku između bilo koje dvije točke izvan zavojnice. Uzmimo jednu točku na jednoj strani zavojnice, a drugu točku na drugoj strani zavojnice. Potencijalnu razliku između obiju strana zavojnice možemo proračunati tako da uzmemo u okolnom prostoru jedan put od jedne do druge strane zavojnice i na tom putu izračunamo integral:

$\int _{1}^{2}H_{s}\cdot d\mathbf {s} =V_{1}-V_{2}$

No kod magneta možemo tu potencijalnu razliku izračunati i na najkraćem putu između oba pola - kroz samu zavojnicu. Na jednoj strani šuplje zavojnice stoji naboj + m, na drugoj -m. Plošna gustoća naboja na sloju jednaka je omjeru naboja i površine sloja: m/f. Magnetsko polje u prostoru između sloja jednako je kao i kod električnog kondenzatora plošnoj gustoći pomnoženoj sa 4∙π:

$H=4\cdot \pi \cdot \omega =4\cdot \pi \cdot {\frac {m}{f}}$

Potencijalna razlika između oba sloja jednaka je umnošku tog polja i udaljenosti d između oba sloja:

$V_{1}-V_{2}=H\cdot d=4\cdot \pi \cdot {\frac {m}{f}}\cdot d$

Pri prolazu kroz dvostruki sloj skače potencijal za vrijednost 4∙π∙ω∙d.

Ovoliku potencijalnu razliku mora dati i integral od jedne do druge strane zavojnice po krivulji koja prolazi prostorom izvan zavojnice. Za polje zatvorene struje možemo odmah napisati koliko ta potencijalna razlika iznosi. Integral uzduž zatvorene kružnice koja ovija električnu struju jednak je:

$\int H_{s}\cdot d\mathbf {s} =4\cdot \pi \cdot {\frac {I}{c}}$

U tom integralu možemo ispustiti mali put kroz zamišljenu zavojnicu, a da se zbog toga vrijednost integrala znatno ne promijeni. No tada nam taj integral znači razliku (diferenciju) potencijala s jedne i druge strane zavojnice, a ta razlika mora biti jednaka gornjem izrazu. Iz jednadžbe:

$4\cdot \pi \cdot {\frac {m}{f}}\cdot d=4\cdot \pi \cdot {\frac {I}{c}}$

dobivamo da magnetski moment magneta koji bi imao isto polje kao i struja mora biti jednak:

$\mu =m\cdot d={\frac {I\cdot f}{c}}$

Zatvorena električna struja djeluje kao magnet čiji je magnetski moment proporcionalan umnošku jakosti struje i površine, omeđene strujom.

U atomu vrte se elektroni oko jezgre. Njihova gibanja moraju izazvati magnetske momente. Razmotrimo sada magnetski moment što ga stvara elektron koji se vrti oko atomske jezgre. Po definiciji struja je jednaka količini naboja koji proteče u sekundi. Elektron stvara prema tome električnu struju e∙v jer v puta prođe u sekundi kroz presjek svoje staze. Magnetski moment elektrona jednak je:

$\mu ={\frac {1}{c}}\cdot e\cdot v\cdot f={\frac {1}{c}}\cdot e\cdot {\frac {f}{\tau }}$

gdje je: τ - vrijeme jedne ophodnje, jednako 1/v. Omjer između površine f i vremena ophodnje τ proporcionalan je impulsu vrtnje. To je lako uvidjeti. Impuls vrtnje je za kružno gibanje dan umnoškom r∙m∙v. Brzinu možemo izraziti umnoškom polumjera i kutne brzine φ. Za impuls vrtnje dobivamo:

$p_{\phi }=m\cdot r^{2}\cdot {\frac {\mathrm {d} {\boldsymbol {\phi }}}{\mathrm {d} {\boldsymbol {t}}}}$

No 1/2∙r²∙dφ je diferencijal površine. Po drugom Keplerovom zakonu je omjer 1/2∙r2∙dφ : dt konstantan. Mjesto omjera diferencijala možemo, dakle, staviti omjer čitave površine i vremena ophodnje:

${\frac {1}{2}}\cdot r^{2}\cdot \mathrm {d} {\boldsymbol {\phi }}:\mathrm {d} {\boldsymbol {t}}=f:\tau$

Odatle se vidi da je impuls vrtnje jednak:

$p_{\phi }=m\cdot r^{2}\cdot {\frac {\mathrm {d} {\boldsymbol {\phi }}}{\mathrm {d} {\boldsymbol {t}}}}=2\cdot m\cdot {\frac {f}{\tau }}$

Ovaj opći odnos vrijedi kod svih staza elektrona. Uvrstimo li u gornju jednadžbu za omjer površine i vremena ophodnje impuls vrtnje, dobivamo:

$\mu ={\frac {e}{2\cdot c\cdot m}}\cdot p_{\phi }$

Ovaj važan odnos postoji u klasičnoj teoriji između magnetskog momenta i impulsa vrtnje. Ona nam pokazuje ujedno porijeklo magnetskih momenata. Oni su prouzrokovani impulsima vrtnje.