Paralelogram vektora
Paralelogram vektora je geometrijski način zbrajanja vektora. Ako se dva vektora [math]\displaystyle{ \overrightarrow{F_1} }[/math] i [math]\displaystyle{ \overrightarrow{F_2} }[/math] predoče usmjerenim dužinama sa zajedničkim hvatištem, njihov se zbroj:
- [math]\displaystyle{ \overrightarrow{F} = \overrightarrow{F_1} + \overrightarrow{F_2} }[/math]
može predočiti kao dijagonala paralelograma kojemu su [math]\displaystyle{ \overrightarrow{F_1} }[/math] i [math]\displaystyle{ \overrightarrow{F_2} }[/math] dvije stranice. Prema vrsti vektorskih veličina postoje posebni nazivi: paralelogram sila, paralelogram brzina i drugo. [1]
Obnovivši grčku statiku, prodrla je renesansna fizika u razdoblju od dva stoljeća do općeg određivanja zakona o ravnoteži. Od velikog značenja bilo je ispitivanje ravnoteže utega na kosim ravninama. Mogu se spojiti dva utega koncem i ispitivati kada na različitim kosinama međusobno drže ravnotežu. Nakon takvih ispitivanja, S. Stevin je došao do najvažnijeg pravila statike, paralelogram o sastavljanju sila. Po tom pravilu mogu se uvijek dvije sile koje djeluju na jedno fizikalno tijelo zamijeniti jednom silom. I obrnuto: svaka sila može se rastaviti na dvije sile. Sile se mogu geometrijski prikazati strelicama (vektorima) koje imaju smjer sila, a dužine jednake veličinama sila. Djeluju li u jednoj točki dvije sile istog smjera, tada se u tom njihovom smjeru zbrajaju djelovanja obiju sila. Djeluju li naprotiv na jedno tijelo dvije sile različitog smjera, rezultat je djelovanja tih dviju sila nova sila, koja ima smjer djelovanja između smjerova obiju sila. Prikažemo li dvije prve sile kao stranice paralelograma, ta je nova sila jednaka dijagonala paralelograma. To sastavljanje sila po pravilu paralelograma jedan je od najdubljih zakona fizike.
Pravilo paralelograma ne vrijedi samo za sile već i za niz fizikalnih veličina kao brzine, ubrzanje (akceleracije), električna i magnetska polja. Sve te fizikalne veličine imaju pored nekog iznosa i neki smjer, pa se mogu geometrijski prikazati vektorima ili strelicama. Zakon o sastavljanju sila bio je osnovni element za opće formuliranje zakona ravnoteže. [2]
Grafičko predočivanje sile
Svaka sila ima svoje hvatište, veličinu (jakost ili intenzitet), pravac i smjer u kome djeluje. Tako na primjer sila teža, kojom Zemlja privlači sva fizikalna tijela, djeluje okomito prema središtu Zemlje. Točka u kojoj sila djeluje zove se hvatište sile, a njen pravac - pravac djelovanja. Smjer sile određujemo strelicom. Tako je na slici točka A hvatište sile. Grafičku silu predočujemo dužinom i smjerom u određenom mjerilu.
Sila je, dakle, određena:
Ovakve veličine koje su određene svojom veličinom (jakošću ili intenzitetom) i smjerom zovu se vektori. To su na primjer sila, brzina, ubrzanje i tako dalje. Ostale veličine koje nemaju smjera, a potpuno su određene svojom veličinom (jakošću ili intenzitetom), zovu se skalari. To su na primjer temperatura, vrijeme i tako dalje. [3]
Sastavljanje sila koje djeluju u istom pravcu
Vuku li da čovjeka jedna kolica, onda je ukupna sila kojom se kolica vuku jednaka zbroju sila oba čovjeka, to jest zbroj tih sila može zamijeniti obje sile. Znači, kad dvije sile djeluju na jedno fizikalno tijelo, onda se one mogu zamijeniti jednom silom koja ima isto djelovanje kao ove spomenute sile. Takva se sila zove rezultanta datih sila, a same sile njenim komponentama. Pronalaženje rezultante zadanih sila zove se sastavljanje sila.
Djeluju li dakle sile [math]\displaystyle{ \overrightarrow{F_1} }[/math] i [math]\displaystyle{ \overrightarrow{F_1} }[/math] ili više njih u istom pravcu i u istom smjeru, rezultanta [math]\displaystyle{ \overrightarrow{F_R} }[/math] jednaka je njihovu zbroju, to jest:
- [math]\displaystyle{ \overrightarrow{F_R} = \overrightarrow{F_1} + \overrightarrow{F_2} +... + \overrightarrow{F_n} }[/math]
Guraju li da čovjeka kolica u suprotnom smjeru, ali u istom pravcu, i to na primjer jedan silom F1 = 70 N, a drugi silom F2 = 50 N, kolica će se gibati u smjeru jačeg djelovanja. Rezultanta će biti jednaka razlici obiju sila, to jest:
- [math]\displaystyle{ F_R = F_1 - F_2 = \mbox{70}\,\mbox{N} - \mbox{50}\,\mbox{N} = \mbox{20}\,\mbox{N} }[/math]
i imat će smjer veće komponente [math]\displaystyle{ \overrightarrow{F_1} }[/math].
Moramo li sastaviti više sila koje djeluju u istom pravcu, ali su suprotnoga smjera, zbrojit ćemo sve sile jednoga i sve sile drugoga smjera, od većeg zbroja odbiti manji i dobiti rezultantu.
Međutim, kad bi zbroj svih sila jednog predznaka bio jednak zbroju svih sila protivnog predznaka, onda bi se djelovanje svih sila poništavalo, i one bi si držale ravnotežu. To isto vrijedi kad na tijelo djeluju samo dvije sile u istom pravcu, protivnog smjera, a po veličini su jednake. Prema tome, da bi dvije sile bile u ravnoteži, moraju biti ispunjeni ovi uvjeti:
- da djeluju u istome pravcu,
- da su suprotnoga smjera,
- da su po veličini jednake.
Poučak o premještanju hvatišta sile
Uzmimo da na neko kruto tijelo djeluje sila [math]\displaystyle{ \overrightarrow{F_1} }[/math] u točki A. U pravcu u kojem ta sila djeluje možemo zamisliti u točki B dvije sile [math]\displaystyle{ \overrightarrow{F_2} }[/math] i [math]\displaystyle{ \overrightarrow{F_3} }[/math] koje su međusobno jednake, a jednake i sili [math]\displaystyle{ \overrightarrow{F_1} }[/math], ali suprotnoga smjera. Ovu pretpostavku možemo učiniti zato što se sile [math]\displaystyle{ \overrightarrow{F_2} }[/math] i [math]\displaystyle{ \overrightarrow{F_3} }[/math] poništavaju, odnosno što si drže ravnotežu. Također se tako poništavaju i sile [math]\displaystyle{ \overrightarrow{F_3} }[/math] i [math]\displaystyle{ \overrightarrow{F_1} }[/math], pa ostaje samo sila [math]\displaystyle{ \overrightarrow{F_2} }[/math]. To je isto kao da smo silu [math]\displaystyle{ \overrightarrow{F_1} }[/math] premjestili iz hvatišta A u hvatište B. Odatle zaključujemo da hvatište sile možemo premjestiti u bilo koju točku u pravcu njena djelovanja.
Paralelogram sila i trokut sila
Svi primjeri do sada su bili kada su sile djelovale u istom pravcu. Drugačija je stvar ako sile čine neki kut. Na primjer, neku splav vuku ljudi na jednoj i drugoj obali rijeke. Pita se kolikom bi silom morao motor tjerati tu splav da nadomjesti vuču ljudi? Traži se, dakle, rezultanta dviju komponenata koje čine kut. Da odredimo rezultantu, nacrtat ćemo sile [math]\displaystyle{ \overrightarrow{F_1} }[/math] i [math]\displaystyle{ \overrightarrow{F_2} }[/math] po veličini i po smjeru u zadanom mjerilu i načiniti paralelogram sila. U tom paralelogramu povući ćemo dijagonalu iz zajedničkog hvatišta obiju sila. Ta dijagonala daje traženu rezultantu. Što je kut koji čine sile manji, to je rezultanta veća. Kad bi kut bio jednak nuli, onda bi rezultanta bila najveća.
Mjesto da crtamo paralelogram sila, možemo nacrtati samo polovinu paralelograma, to jest trokut sila, jer su suprotne stranice u paralelogramu jednake. Kod trokuta sila je bitno da jednu silu nanosimo na drugu po veličini i po smjeru (početak druge sile je na kraju prve sile i tako dalje), a zatim početak prve spojimo sa završetkom zadnje.
Sastavljanje dviju sila s različitim hvatištima
Djeluju li na neko tijelo dvije sile koje nemaju isto hvatište, njihovu ćemo rezultantu naći tako da hvatište tih sila prenesemo u presjecište njihovih pravaca djelovanja. Nakon toga treba konstruirati paralelogram sila i na uobičajen način naći njihovu rezultantu. Ovu metodu sastavljanja sila možemo upotrijebiti samo onda ako se pravci djelovanja sijeku na slici.
Poligon sila
Na jednu kuglu djeluju 4 sile [math]\displaystyle{ \overrightarrow{F_1} }[/math], [math]\displaystyle{ \overrightarrow{F_2} }[/math], [math]\displaystyle{ \overrightarrow{F_3} }[/math] i [math]\displaystyle{ \overrightarrow{F_4} }[/math]. Pita se u kojem će se pravcu i smjeru kugla gibati. Da nađemo rezultantu tih sila, uzet ćemo bilo koju točku O i od nje nacrtati paralelno, iste veličine i istoga smjera silu [math]\displaystyle{ \overrightarrow{F_1} }[/math]. Iz kraja sile [math]\displaystyle{ \overrightarrow{F_1} }[/math] nanijet ćemo isto taku silu [math]\displaystyle{ \overrightarrow{F_2} }[/math]. Sile [math]\displaystyle{ \overrightarrow{F_1} }[/math] i [math]\displaystyle{ \overrightarrow{F_2} }[/math] dat će rezultantu [math]\displaystyle{ \overrightarrow{F_{R12}} }[/math] po trokutu sila. Na silu [math]\displaystyle{ \overrightarrow{F_2} }[/math] nanesimo silu [math]\displaystyle{ \overrightarrow{F_3} }[/math], pa će sila [math]\displaystyle{ \overrightarrow{F_3} }[/math] i [math]\displaystyle{ \overrightarrow{F_{R12}} }[/math] dati rezultantu [math]\displaystyle{ \overrightarrow{F_{R123}} }[/math]. Isto tako na silu [math]\displaystyle{ \overrightarrow{F_3} }[/math] nanesimo silu [math]\displaystyle{ \overrightarrow{F_4} }[/math], pa će sila [math]\displaystyle{ \overrightarrow{F_4} }[/math] i sila [math]\displaystyle{ \overrightarrow{F_{R123}} }[/math] dati rezultantu [math]\displaystyle{ \overrightarrow{F_R} }[/math]. Vidimo da je posve nepotrebno bilo crtanje pomoćnih pomoćnih rezultanta [math]\displaystyle{ \overrightarrow{F_{R12}} }[/math] i [math]\displaystyle{ \overrightarrow{F_{R123}} }[/math]. Dovoljno je sile [math]\displaystyle{ \overrightarrow{F_1} }[/math], [math]\displaystyle{ \overrightarrow{F_2} }[/math], [math]\displaystyle{ \overrightarrow{F_3} }[/math] i [math]\displaystyle{ \overrightarrow{F_4} }[/math] nanijeti jednu na drugu po veličini i po smjeru i početak prve spojiti sa svršetkom posljednje. Dobiveni poligon naziva se poligon sila.
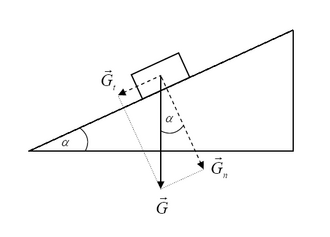
Rastavljanje sile na dvije komponente
Na okretnoj stupnoj dizalici visi teret [math]\displaystyle{ \overrightarrow{G} }[/math]. Da odredimo sile kojima su štapovi AC i BC opterećeni, rastavit ćemo silu [math]\displaystyle{ \overrightarrow{G} }[/math] na komponente [math]\displaystyle{ \overrightarrow{F_1} }[/math] i [math]\displaystyle{ \overrightarrow{F_2} }[/math]. Smjerovi komponenata su pravci štapova, pa možemo nacrtati paralelogram sila kojem je sila [math]\displaystyle{ \overrightarrow{G} }[/math] dijagonala. Iz slike vidimo da komponenta [math]\displaystyle{ \overrightarrow{F_1} }[/math] nastoji rastegnuti štap, pa je štap BC opterećen na vlak. Komponenta [math]\displaystyle{ \overrightarrow{F_2} }[/math] nastoji štap AC stlačiti, stoga je on opterećen na tlak.
Postupak kod kojeg iz zadane sile pronalazimo komponente zove se rastavljanje sila.
Slike
|
Izvori
- ↑ paralelogram vektora, [1] "Hrvatska enciklopedija", Leksikografski zavod Miroslav Krleža, www.enciklopedija.hr, 2017.
- ↑ Ivan Supek: "Nova fizika", "Školska knjiga" 1966.
- ↑ Velimir Kruz: "Tehnička fizika za tehničke škole", "Školska knjiga" Zagreb, 1969.