Keplerovi zakoni

Slika prikazuje 3 Keplerova zakona s dvije planetarne putanje:
(1) Putanje planeta su elipse, sa žarištima F₁ i F₂ za prvi planet i F₁ i F₃ za drugi planet. Sunce je smješteno u žarištu F₁.
(2) Dva zasjenčena područja A₁ i A₂ imaju jednake površine i vrijeme za planet 1 da prekrije područje A₁ je jednako da prekrije područje A₂.
(3) Ukupna ophodna vremena planeta 1 i planeta 2 imaju odnos t₂/t₁ = (a₂/a₁)^3/2.

Keplerovi zakoni opisuju gibanje planeta oko Sunca. Tri su Keplerova zakona:

1. Prvi Keplerov zakon − svi planeti gibaju se po elipsama kojima je jedno od žarišta Sunce.
2. Drugi Keplerov zakon − radijvektor (provodnica) Sunce-planet (dužina koja spaja središte Sunca i trenutni položaj planet), prelazi u jednakim vremenskim razmacima jednake površine.
3. Treći Keplerov zakon − Kvadrati ophodnih vremena planeta proporcionalni su kubovima njihovih srednjih udaljenosti od Sunca.

Gibanje satelita oko matičnog planeta i svaki drugi sličan sustav također se opisuju Keplerovim zakonima. Naziv su dobili po njemačkom astronomu Johannesu Kepleru.

Povijesna bilješka

Obrađujući vrlo precizna promatranja koja je izvršio Tycho Brahe, Kepler je uočio neslaganje kretanja planeta s njihovim pretpostavljenim kružnim putanjama. Analizirajući geometrijski oblik planetskih putanja zaključio je da se planeti ne gibaju oko Sunca po pravilnim kružnicama (kao što je mislio Kopernik), već da su njihove staze, zapravo, (uglavnom blage) elipse i da se po njima planeti kreću po određenim zakonitostima. Usporedivši svoje pretpostavke s rezultatima promatranja, ustanovio je da se vrlo dobro slažu. Tako je formulirao tri najznačajnija zakona kinematike Sunčeva sustava.

Pokazalo se da svi Keplerovi zakoni vrijede i za sustave satelita svakog planeta, odnosno općenito za sve sustave u Svemiru, samo je za svaki od njih konstanta $k$ iz trećega zakona različita. Pošavši od Keplerovih zakona, Newton je postavio temelje ogromnom području nebeske mehanike i posredno utjecao na nagli razvoj matematike, fizike i pojavu sasvim novog pravca u filozofskom tumačenju svijeta.

Prvi Keplerov zakon

Podrobniji članak o temi: Prvi Keplerov zakon

Geometrija planetarnog kretanja: planet ($M$) obilazi oko Sunca ($S$) po elipsi ($P$-perihel, $A$-afel)

Sa smanjenjenjem ekscentriciteta (ε → 0) elipsa prelazi u kružnicu, a njezina velika poluos prelazi u polumjer kružnice. Ulogu srednje udaljenosti ima tada, naravno, sam polumjer kružnice. S druge strane, s povećanjem ekscentriciteta (ε → 1) elipsa prelazi u parabolu. Za hiperbolu vrijedi ε > 1.

Prvi Keplerov zakon glasi:

Planeti se oko Sunca kreću po eliptičnim putanjama; u zajedničkom žarištu tih elipsa nalazi se Sunce.

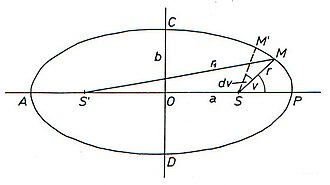
Na prikazanoj slici elipsa predstavlja putanju nekog planeta. Linearni ekscentricitet je:

$e={\overline {OS}}={\overline {OS'}}={\sqrt {a^{2}-b^{2}}}$

a numerički ekscentricitet je:

$\varepsilon ={\frac {e}{a}}={\frac {\sqrt {a^{2}-b^{2}}}{a}}$

Iz toga proizlazi:

${\frac {b^{2}}{a}}=p=a(1-\varepsilon ^{2})$

gdje se $p$ naziva parametrom elipse.

Po definiciji elipse, $r+r_{1}=2a$. Iz trokuta $S'SM$, primjenom kosinusnog poučka i supstitucijom parametra elipse, slijedi da je:

$r={\frac {p}{1+\varepsilon \cos v}}$

i to bi bila jednadžba planetske putanje (jednadžba elipse), odnosno matematski izraz prvoga Keplerova zakona. Iz te se jednadžbe vidi ovisnost udaljenosti planeta od Sunca o kutu $v$ koji se naziva pravom anomalijom planeta.

Kad je $v={\frac {\pi }{2}}$, tada je $r=p$, pa iz toga proizlazi definicija parametra planetske putanje kao radijus-vektora planeta koji je okomit na glavnu os elipse.

Karakteristične točke planetske putanje su afel i perihel (označene na slici s $A$ i $P$). Afel je točka u kojoj je planet najudaljeniji od Sunca, a perihel je točka u kojoj je planet najbliži Suncu. Ako je $a$ srednja udaljenost planeta od Sunca, onda proizlazi da su:

$A=a(1+\varepsilon )$

$P=a(1-\varepsilon )$

Drugi Keplerov zakon

Podrobniji članak o temi: Drugi Keplerov zakon

Radijvektor (provodnica) Sunce-planet opisuje u jednakim vremenskim razmacima jednake površine (plava površina). Zelena strelica prikazuje brzinu (vektor brzine). Ljubičasta strelica usmjerena prema Suncu prikazuje ubrzanje (ostale dvije ljubičaste strelice su komponente ubrzanja, jedna okomita i druga paralelna (normalna) s brzinom.

Drugi Keplerov zakon glasi:

Radijvektor (provodnica) Sunce-planet opisuje u jednakim vremenskim razmacima jednake površine.

Na prikazanoj slici $dv$ je priraštaj kuta $v$ koji odgovara kratkom intervalu $dt$. Za to vrijeme radijus-vektor prebriše površinu:

$dp={\frac {r^{2}\pi }{2\pi }}dv={\frac {1}{2}}r^{2}dv$

($v$ u radijanima), jer, s obzirom na to da je priraštaj $dv$ vrlo malen, može se površina isječka elipse smatrati površinom isječka kruga s polumjerom $r$. Tako proizlazi:

${\frac {dp}{dt}}={\frac {1}{2}}r^{2}{\frac {dv}{dt}}$

${\frac {dp}{dt}}$ naziva se površinskom brzinom. Prema drugom Keplerovu zakonu ta je brzina konstantna:

$r^{2}{\frac {dv}{dt}}=C$

i to je matematički izraz drugoga Keplerova zakona.

Treći Keplerov zakon

Podrobniji članak o temi: Treći Keplerov zakon

Kretanje Sunca (žuto), Zemlje (plavo) i Marsa (crveno) prema heliocentričnom sustavu (lijevo) i geocentričnom sustavu (desno).
Napomena: putanje planeta su kružnice prema Kopernikovom sustavu i putanja Marsa je 2 godine (umjesto stvarnih 1.88 godina) zbog jednostavnosti.

Treći Keplerov zakon glasi:

Kvadrati ophodnih vremena srazmjerni su kubovima srednjih udaljenosti (velikih poluosi elipse) planeta od Sunca

${\frac {a^{3}}{T^{2}}}=k$

gdje je $k$ jedan te isti broj za sve planete. Ako se za jedinicu udaljenosti uzme 1 a. j., a za jedinicu vremena jedna godina, matematski izraz trećega Keplerova zakona poprima oblik:

${a^{3}}={T^{2}}$

Treći Keplerov zakon jasno povezuje udaljenosti planeta s njihovim sideričkim periodima.