Treći Keplerov zakon

Veza između sideričkog i sinodičkog perioda ($S$-Sunce, $Z$-Zemlja, $P$-gornji planet)

Kretanje Sunca (žuto), Zemlje (plavo) i Marsa (crveno) prema heliocentričnom sustavu (lijevo) i geocentričnom sustavu (desno).
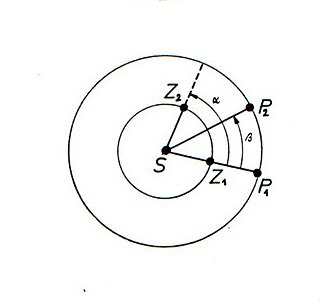
Napomena: putanje planeta su kružnice prema Kopernikovom sustavu i putanja Marsa je 2 godine (umjesto stvarnih 1.88 godina) zbog jednostavnosti.

Newtonov zakon gravitacije: Dva nebeska tijela se privlače uzajamno silom koja je proporcionalna (u skladu) umnošku njihovih masa, a obrnuto proporcionalna kvadratu njihove međusobne udaljenosti.

Venera (žuta kružnica) obiđe Sunce za 0.615 godine ili 224.65 dana. Prosječna udaljenost Venereod Sunca je ono 108 milijuna kilometara (ono 0.7 AJ).

Newtonov zakon gravitacije je pomogao da se pronađe planet Neptun. Usporedba Zemlje i Neptune.

Prema Općoj teoriji relativnosti, planet u svom obilasku oko Sunca opisuje elipsu koja se polako okreće u svojoj ravnini.

Treći Keplerov zakon glasi:

Kvadrati ophodnih vremena srazmjerni su kubovima srednjih udaljenosti (velikih poluosi elipse) planeta od Sunca

${\frac {a^{3}}{T^{2}}}=k$

gdje je $k$ jedan te isti broj za sve planete. Ako se za jedinicu udaljenosti uzme 1 a. j., a za jedinicu vremena jedna godina, matematski izraz trećega Keplerova zakona poprima oblik:

${a^{3}}={T^{2}}$

Treći Keplerov zakon jasno povezuje udaljenosti planeta s njihovim sideričkim periodima. Promatrači sa Zemlje mogu izravno opažati samo sinodički period. Veza između sideričkog ($T$) i sinodičkog ($S$) perioda nekog planeta, uz poznat period Zemljina obilaska oko Sunca ($E$) je:

za gornje planete:

${\frac {1}{S}}={\frac {1}{E}}-{\frac {1}{T}}$

za donje planete:

${\frac {1}{S}}={\frac {1}{T}}-{\frac {1}{E}}$

odnosno, općenito:

${\frac {1}{T}}={\frac {1}{S}}\mp {\frac {1}{E}}$

Treći Keplerov zakon u modernom obliku

Treći Keplerov zakon se može napisati u modernom obliku kao:

${\frac {T^{2}}{r^{3}}}={\frac {4\pi ^{2}}{GM}}$

gdje je: T - ophodno vrijeme planeta, M - masa zvijezde, G - gravitacijska konstanta i r - polumjer (velika poluos elipse). U punom obliku prema Newtonovom zakonu gravitacije, M bi trebalo zamijeniti s:

$M+m,$

gdje je: m - masa planeta koji obilazi zvijezdu. U stvarnosti, konstanta proporcionalnosti nije sasvim jednaka za sve planete. Ipak, ako je m dovoljno mala u odnosu na M, približenje je sasvim dobro.

Povijest

S prva dva Keplerova zakona opisano je gibanje planeta. Kepler je htio riješiti još jedno veliko pitanje, naći u kakvom odnosu stoje vremena ophoda planeta prema njihovim udaljenostima od Sunca. Nije bilo dosta reći da Venera obiđe Sunce u kraćem vremenu negoli Zemlja zato što mu je bliže, nego je trebalo naći brojeve koji točno označuju taj odnos za sve planete. Ophodna vremena planeta bila su odavna poznata. Ustanovljeno je opažanjima da :

• Merkur obiđe Sunce za 0.241 godine ili 88 dana
• Venera obiđe Sunce za 0.615 godine ili 225 dana
• Zemlja obiđe Sunce za 1 godinu ili 365.25 dana
• Mars obiđe Sunce za 1.881 godinu ili 687 dana
• Jupiter obiđe Sunce za 11.86 godina ili 4332.6 dana
• Saturn obiđe Sunce za 29.46 godina ili 10759.2 dana

Kepler je na razne načine pokušavao dovesti u vezu ove brojeve sa srednjim udaljenostima planeta. Napokon mu je uspjelo utvrditi zanimljivu i važnu činjenicu, da je za svaki planet kvadrat ophodnog vremena bio gotovo jednak trećoj potenciji njegove srednje udaljenosti od Sunca. Na primjer ophodno vrijeme Marsa je zabilježeno da iznosi 1.881 godine. Ako izračunajmo kvadrat tog broja, dobivamo 1.881 * 1.881 = 3.538. Srednja je udaljenost Marsa od Sunca jednaka 1.524. Treća potencija ovog broja je 1.524 * 1.524 * 1.524 = 3.540. Takav račun se može provesti za sve planete.

Tablica ispod pokazuje Kopernikove i današnje rezultate (osnova je udaljenost Zemlje od Sunca a_Z):

Odnos a/aZ	Kopernik	Danas
Merkur	0.376	0.387
Venera	0.7196	0.723
Mars	1.52	1.524
Jupiter	5.217	5.203
Saturn	9.184	9.54

Newtonov zakon gravitacije

Podrobniji članak o temi: Newtonov zakon gravitacije

Prva teorija gravitacije započinje 1687., kada je Isaac Newton objavio svoje glavno djelo Matematička načela prirodne filozofije (Philosophiae naturalis principia mathematica). Newton temelji svoja razmatranja na osnovu Keplerovih zakona. Newton je zamišljao da bi se Zemljina sila gravitacije morala protezati do Mjeseca. Ako se računa kolika ta privlačna sila Zemlje mora biti da Mjesec prisili na njegovu (približno) kružnu stazu, izlazi da je privlačna sila obrnuto proporcionalna kvadratu udaljenosti od Zemljina težišta. Prenoseći taj rezultat na sva nebeska tijela, Newton postavlja svoj Newtonov zakon gravitacije. Pri tome se masa nebeskog tijela zamišlja koncentrirana u točki. Newton dokazuje da tijelo sa sferno simetričnim rasporedom mase (a takva su približno sva nebeska tijela) djeluje kao da je sva njegova masa koncentrirana u njegovu središtu.

Iz Općeg zakona gravitacije dobiveni su matematički izrazi za Keplerove zakone, pa tako treći Keplerov zakon za dva planeta točnije glasi:

${\frac {a_{1}^{3}}{a_{2}^{3}}}\ ={\frac {T_{1}^{2}(M+m_{1})}{T_{2}^{2}(M+m_{2})}}\$

gdje su: a₁, a₂ - velike osi putanja tih planeta, T₁, T₂ - ophodna vremena tih planeta, a m₁, m₂ - mase tih planeta, koje su malene prema M - masa Sunca. Ako se mase m₁, m₂ zanemare prema M, posljednji razlomak je jednak 1, pa izlazi treći Keplerov zakon u izvornom obliku:

${\frac {a^{3}}{T^{2}}}=k$

Uzme li se u obzir djelovanje međusobnog privlačenja planeta (račun smetnji ili pertubacija), dobiva se izuzetno točno slaganje s astronomskim opažanjima. Tako je na temelju nepravilnosti u gibanju planeta Urana računom smetnji određeno mjesto novog planeta. Taj su račun nezavisno izvršili Francuz Urban Le Verrier (1811. – 1877.) i Englez John Couch Adams (1819. – 1892.). Na temelju toga našao je Johann Gottfried Galle (1812. –1910.) taj planet 1846., koji je dobio ime Neptun.

Račun smetnji, među ostalima, pokazuje da se eliptična putanja planeta Merkur mora polagano okretati oko Sunca, u istom smjeru u kojem Merkur obilazi Sunce. Taj račun smetnji daje zakretanje za otprilike 532 lučne sekunde u stoljeću, ali opažanja daju zakretanje koje je za 43 lučne sekunde veće. To maleno razilaženje između Newtonove teorije gravitacije i astronomskih opažanja objašnjava tek Einsteinova Opća teorija relativnosti.

Treći Keplerov zakon za sustav dviju masa

Podrobniji članak o temi: Problem dvaju tijela

Dvojna zvijezda Sirius A i B.

Treba zbrojiti izraze za ubrzanje prvog i drugog tijela, i to njihove desne jednakosti, ali tako da uvedemo zbroj polumjera (r₁ + r₂ = r):

$g_{1}=G{\frac {M_{2}}{r^{2}}}\$

$g_{2}=G{\frac {M_{1}}{r^{2}}}\$

Proizlazi:

${\frac {r^{3}}{P^{2}}}={\frac {G}{4\pi ^{2}}}\cdot (M_{1}+M_{2})$

U konstanti trećeg Keplerova zakona nalazi se ukupna masa dvojnog sustava!

U općenitijem slučaju, tijela se gibaju po eliptičnim stazama. Pritom su ispunjeni neki geometrijski uvjeti. Ekscentricitet obiju staza je jednak, smjer velikih poluosi se podudara, a tijela su na stazama uvijek dijametralno suprotno onom žarištu u kojem je centar mase. Kod koncentričnih kružnica koje su razmatrane prije, razmak tijela ima istu ulogu koju kod eliptičnih staza ima srednji razmak (zbroj velikih poluosi), dok putanjska brzina ima ulogu srednje brzine.

Poveznice

• Johannes Kepler
• Keplerovi zakoni
• Ophodno vrijeme
• Prividno gibanje planeta
• Prvi Keplerov zakon
• Drugi Keplerov zakon