Johann Jakob Balmer

1. PREUSMJERI Predložak:Infookvir znanstvenik

Johann Jakob Balmer, (Lausen, Basel-Landschaft, Švicarska, 1. svibnja 1825. – Basel, Švicarska, 12. ožujka 1898.), švicarski fizičar i matematičar. Doktorirao (1849.) na Sveučilištu u Baselu, gdje je i bio zaposlen (od 1865. do 1890.). Godine 1885. pronašao je matematički izraz (Balmerova jednadžba) s pomoću kojega su se mogle izračunati tada poznate valne duljine λ linija u vidljivom dijelu vodikova spektra (Balmerova serija: 656,3 nm, 486,1 nm, 434,1 nm i 410,2 nm):

$\lambda \ =B\cdot {\frac {n^{2}}{n^{2}-2^{2}}}$

gdje je: B - konstanta vrijednosti 364,5 nm, a n - cijeli broj veći od 2 (u spektru vidljive svjetlosti n = 3, 4, 5 ili 6) i predvidjeti valne duljine u nevidljivom dijelu vodikova spektra. Usavršavanjem spektrografskih aparata Balmerova serija proširila se na ultraljubičaste linije (397,0 nm, 388,9 nm, 383,5 nm, 364,6 nm i drugo) vodikova spektra. Godine 1888. J. Rydberg poopćio je Balmerovu jednadžbu a s pomoću nje otkrivene su Lymanova (od 1906. do 1914.), Paschenova (1908.), Brackettova (1922.) i Pfundova (1924.) serija. U okviru svojega modela atoma N. Bohr je (1913.) teorijski protumačio Balmerovu jednadžbu. Ona je značajno pridonijela razvoju kvantne fizike. Po njem je nazvan krater na Mjesecu (Balmer (krater)).

Balmerova serija

Podrobniji članak o temi: Balmerova serija

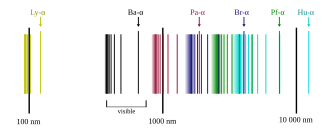
Balmerova serija u atomskoj fizici prestavlja jednu od emisionih spektralnih linija vodika, koja nastaje skokom elektrona iz viših kvantnih energetskih razina u niže kvantne energetske razine. Balmerovu seriju se može izračunati sa Balmerovom jednadžbom, a to je iskustvena jednadžba koju je otkrio J. J. Balmer 1885. Vidljivi dio spektra vodika pokazuje četiri valne duljine: 410 nm, 434 nm, 486 nm i 656 nm, i prestavljaju emisiju fotona, koja nastaje skokom elektrona sa više energetske razine na energetsku razinu 2. Jedan dio Balmerove serije je u ultraljubičastom dijelu spektra, jer je valna duljina manja od 400 nm.

Vidljivi dio spektralnih linija vodika prestavljene Balmerovom serijom. H-alfa je crvena linija na desno. Dvije krajnje lijeve linije su ultraljubičaste, jer imaju valnu duljinu kraću od 400 nm.

Iskustvene činjenice o spektrima

Podrobniji članak o temi: Spektar (fizika)

Užarena čvrsta tijela emitiraju svjetlost s kontinuirano raspodijeljenim valnim duljinama (toplinsko zračenje).

Vodikove spektralne linije, u logaritamskoj skali.

Prijelaz elektrona i njihova rezultirajuća valna duljina za vodik (Bohrov model atoma).

Emisijski spektar natrija koji prikazuje svojstvenu D liniju.

Sunčev spektar sa Fraunhoferovim linijama.

U pojednostavljenom Bohrovom modelu atoma vodika, Balmerova serija nastaje skokom elektrona na drugu energetsku razinu (n = 2). Prikazana je emisija svjetlosti. Prijelaz elektrona prestavlja H-alfa, prvu liniju Balmerove serije, valne duljine 656 nm.

Lymanova serija vodikovog atoma u ultraljubičastom području.

Dvije Balmerove linije (α i β) se jasno vide u emisijskom spektru deuterijeve svjetiljke.

Emisijski spektar željeza.

Dijagram energetske razine elektrona u vodikovom atomu.

Užarena čvrsta tijela emitiraju svjetlost s kontinuirano raspodijeljenim valnim duljinama (toplinsko zračenje). Od temperature užarenog tijela zavisi koji je dio spektra najjači (najintenzivniji), ali od mjesta maksimuma postepeno se gasi svjetlost prema manjim i većim valnim duljinama. Nasuprot tome kontinuiranom spektru čvrstih tijela opaža se kod plinova i para nešto drugo. U njihovu se spektru pojavljuju diskretne linije, koje su svojstvene za pojedine kemijske elemente. Čitav spektar se sastoji od niza oštro određenih linija.

Lako je uvidjeti da linijski spektar potječe od atoma. Takvi se spektri dobivaju pri pokusima s katodnim i kanalnim zrakama. Električno izbijanje u katodnoj cijevi niskog tlaka izaziva uvijek velik broj atoma na emisiju svjetlosti. Linijske spektre emitiraju također i plemeniti plinovi, koji se sastoje od čistih atoma, a ne molekula.

Linijske spektre možemo studirati na emisijskom ili apsorpcijskom spektru. Pusti li se bijela svjetlost kroz neke pare ili plin, opaža se u dobivenom spektru da su neke valne duljine ugušene. Tamne linije stoje točno na onim mjestima spektra gdje bi ležale emisijske linije. Plin dakle apsorbira svjetlost onih valnih duljina koje bi inače emitirao. Apsorpcijski spektar slaže se potpuno s emisijskim. Ova određenost u spektrima kemijskih elemenata jedan je od temeljnih zakona nuklearne fizike.

Iako svakom kemijskom elementu pripadaju posebne, svojstvene spektralne linije, ipak se u njihovim spektrima opažaju neka zajednička svojstva, koja omogućuju da se unese red u golem spektroskopski materijal. Spektralne linije svakog kemijskog elementa daju se srediti u nekoliko serija. Svaka pojedina serija predstavlja niz linija koje su poredane po određenom pravilu. Često se već na prvi pogled vidi da linije jedne serije pripadaju zajedno. Promatramo li linije od većih valnih duljina prema manjim, udara nam odmah u oči da se razmak između njih smanjuje. Linije se gomilaju prema određenoj valnoj duljine, koja je granica te serije.

Prvi je J. J. Balmer 1885. otkrio da se vodikov spektar može prikazati jednostavnom matematičkom jednadžbom. Njemu su tada bile poznate 4 vidljive vodikove linije s valnim duljinama:

• H_α = 656, 199 nm
• H_β = 486, 152 nm
• H_γ = 434, 067 nm
• H_δ = 410, 194 nm

Običaj je da se vodikove linije označe početnim slovima grčkog alfabeta, koja dolaze kao indeksi kemijskom simbolu H. Recipročne vrijednosti valnih duljina tih četiriju linija daje se jednadžbom (Rydbergova formula):

${\frac {1}{\lambda }}=R\cdot \left({\frac {1}{2^{2}}}-{\frac {1}{m^{2}}}\right)$

gdje je: m = 3, 4, 5, 6; a R je takozvana Rydbergova konstanta. Uvrstimo li u Balmerovoj jednadžbi za m cijele brojeve veće od 7 dobivamo valne duljine koje leže u ultraljubičastom području spektra. Pokusima se doista našlo još oko 30 linija koje se potpuno slažu s Balmerovom jednadžbom. Linije se gomilaju prema valnoj duljini koja je dana izrazom:

${\frac {1}{\lambda }}={\frac {R}{2^{2}}}$

To je granica serije. Balmerova serija je idealni tip spektralnih linija uopće. Kako se vidi na slici, razmak između susjednih linija pravilno se smanjuje, i linije se gomilaju prema određenoj granici.

Iz razloga koji će se kasnije iznijeti uvedeno je da se spektralne jednadžbe postavljaju za frekvencije, a ne za valne duljine. Pokusima se, doduše, mjere valne duljine (iz interferentnih, ogibnih ili disperzionih pojava), ali zakoni spektralne analize postaju pregledniji kad se uzimaju u obzir frekvencije. Pri tom treba misliti na slijedeće: frekvencija ν se može izračunati iz valne duljine λ prema poznatom odnosu:

$\nu \cdot \lambda =c$

No brzina svjetlosti c nije tako točno izmjerena kako su točna mjerenja valne duljine. Točnost spektralne analize je nenadmašiva. Iz tog razloga i dalje se u spektralnoj analizi svi iskustveni podaci izražavaju u valnim duljinama.

Uvodeći frekvenciju, možemo Balmerovu jednadžbu pisati u obliku:

$\nu ={\frac {c}{\lambda }}=c\cdot R\cdot ({\frac {1}{2^{2}}}-{\frac {1}{m^{2}}})$

gdje je m = 3, 4, 5…. Frekvencije spektralnih linija vodika mogu se dakle prikazati kao razlike (diferencije) između dva člana, od kojih je prvi konstantan, a drugi opada kao 1/9, 1/16, 1/25, 1/36 …. Tu se odmah nameće pitanje: Mora li se uvijek uzeti kao konstantan broj 1/4? Moguće je pomisliti, da prvi konstantni član bude bilo koji razlomak 1/n². Godine 1908. našao je F. Paschen u infracrvenom području spektralne linije vodika kojima su se valne duljine točno slagale s izrazima:

${\frac {1}{\lambda }}=R\cdot ({\frac {1}{3^{2}}}-{\frac {1}{4^{2}}})$

${\frac {1}{\lambda }}=R\cdot ({\frac {1}{3^{2}}}-{\frac {1}{5^{2}}})$

Tu dakle imamo dva člana jedne serije, kojoj je konstantni član R/3². Taj član ujedno određuje i granicu serije. I od te takozvane Paschenove serije nađen je vrlo velik broj linija. Godine 1916. pronašao je Lyman na drugoj strani od Balmerove serije, duboko u ultraljubičastom području, nove spektralne linije, koje smo mogli prikazati istom Balmerovovom jednadžbom, samo što je za konstantni član trebalo uzeti u nazivniku cijeli broj 1. Vodikov spektar sastoji se, od ovih serija:

Lymanova serija:

$\nu =c\cdot R\cdot ({\frac {1}{1^{2}}}-{\frac {1}{m^{2}}})$

gdje je: m = 2, 3, 4 ….

Balmerova serija:

$\nu =c\cdot R\cdot ({\frac {1}{2^{2}}}-{\frac {1}{m^{2}}})$

gdje je: m = 3, 4, 5 ….

Paschenova serija:

$\nu =c\cdot R\cdot ({\frac {1}{3^{2}}}-{\frac {1}{m^{2}}})$

gdje je: m = 4, 5, 6 ….

Brackettova serija:

$\nu =c\cdot R\cdot ({\frac {1}{4^{2}}}-{\frac {1}{m^{2}}})$

gdje je: m = 5, 6, 7 ….

Pfundova serija:

$\nu =c\cdot R\cdot ({\frac {1}{5^{2}}}-{\frac {1}{m^{2}}})$

gdje je: m = 6, 7, 8 ….

Od tog golemog mnoštva linija padaju u vidljivo područje spektra svega prve 4 linije Balmerove serije. Odatle se vidi kako je važno ispitivati čitav spektar da se nađu osnovni zakoni serije.

Frekvencije spektralnih linija vodika možemo općenito izraziti jednadžbom:

$\nu ={\frac {c\cdot R}{n^{2}}}-{\frac {c\cdot R}{m^{2}}}$

gdje su: n i m - cijeli brojevi.

Frekvencije vodikovih linija dobiju se, dakle, da se od niza c∙R/n² učine sve moguće pozitivne razlike (diferencije). Tako objašnjena, Balmerova jednadžba vodi nas do općeg načela kombinacije, što ga je otkrio W. Ritz 1908. Po tom načelu dade se za svaki kemijski element postaviti niz terma T₁, T₂, T₃, …. tako da su frekvencije njegova spektra dane razlikama (diferencijama):

$\nu =T_{m}-T_{n}$

Ritzovo načelo kombinacije potvrđeno je pri ispitivanju svih spektara. Ono je ključ za sređivanje različitih serija. Načelo kombinacije sadrži u sebi osnovni zakon prirode, koji se u punom smislu razotkriva tek u nuklearnoj fizici.