Fraktalna dimenzija

Fraktalna dimenzija je vrijednost koja nam daje uvid u to u kojoj mjeri neki fraktal ispunjava prostor u kojem se nalazi. Postoji mnogo definicija fraktalne dimenzije, od kojih se niti jedna ne može smatrati univerzalnom. Najjednostavnija je dimenzija samosličnosti, ali se ona može upotrijebiti samo kod vrlo jednostavnih geometrijskih fraktala. Za teoriju je najvažnija Hausdorffova dimenzija, a u praksi se najviše koristi Minkowski-Bouligandova dimenzija.

Uvod

Kako mjeriti fraktale? Uzmimo za primjer Kochovu krivulju. To je krivulja, pa bi bilo logično mjeriti njezinu duljinu, u metrima. Mjerit ćemo ju na način na koji mjerimo ostale nepravilne krivulje – aproksimacijom. Uzimamo sve manje i manje dužine i stavljamo ih uz krivulju te nam zbroj njihovih duljina daje aproksimaciju duljine krivulje. Pokušajmo istom metodom izmjeriti duljinu Kochove krivulje. Recimo da je prvi segment duljine 1m. To nam ne daje dovoljnu preciznost, pa uzimamo manje segmente. Nakon prve iteracije imamo četiri segmenta duljine 1/3 m. Zbroj tih segmenata daje nam duljinu od 4/3 m. Ako nastavimo dalje, krivulja će nakon treće iteracije imati duljinu 16/9 m. Matematičkom indukcijom dolazimo do opće formule ${\mathit {L}}=\left({\frac {4}{3}}\right)^{n}$ , ako je n broj iteracija. Kod krivulje iz našeg primjera (s prvim segmentom duljine 1m) duljina krivulje nakon 128 iteracija bila bi približno jednaka jednoj svjetlosnoj godini (9.46∙10¹⁵m). Pošto "prava" Kochova krivulja ima beskonačno mnogo iteracija, dolazimo do zaključka da je njezina duljina beskonačna, kao i duljina svakog njenog segmenta.

Očito smo se prevarili u pokušaju mjerenja duljine Kochove krivulje, ali bismo joj možda mogli izmjeriti površinu, u kvadratnim metrima. Opet ćemo se poslužiti metodom aproksimacije. Nakon prve iteracije, aproksimacija površine je trokut površine ${\frac {\sqrt {3}}{12}}$ . Sljedeće iteracije daju po četiri puta više sličnih trokuta devet puta manje površine. Opća formula površine glasi ${\frac {\sqrt {3}}{12}}\cdot \left({\frac {4}{9}}\right)^{n}$ . Kada n teži u beskonačno, drugi faktor (a time i cijela površina) teži nuli. Vidimo da površina Kochove krivulje ne postoji. Pa, ako ne možemo mjeriti ni duljinu ni površinu, kako možemo mjeriti fraktale?

Vidimo da je Kochova krivulja "prevelika" da bi bila jednodimenzionalna linija, a "pretanka" da bi bila dvodimenzionalna površina. Dakle, vrijednost njezine dimenzije bi trebala biti negdje između jedan i dva. Na neki način, za Kochovu krivulju moramo naći mjernu jedinicu, m^d, koja je "između" metra i kvadratnog metra. Za d uzimamo vrijednost fraktalne dimenzije.

Dimenzija samosličnosti

Dimenzija samosličnosti koristi promjenu mjere (duljine, površine, volumena...) u odnosu na mijenjanje broja iteracija kod potpuno samosličnih fraktala. Kod Kochove krivulje svaka sljedeća iteracija daje četiri puta više segmenata tri puta manje duljine. Ako broj segmenata označimo s N, a duljinu segmenta s L, ukupna će duljina krivulje biti NL. Za Kochovu krivulju stoga vrijedi $4{\mathit {N}}\left({\frac {\mathit {L}}{3}}\right)={\mathit {N}}{\mathit {L}}^{\mathit {d}}$ , ako za mjeru duljine uvrstimo spomenuti "d-dimenzionalni metar", md. Preuređivanjem jednadžbe dobivamo ${\mathit {d}}=\log _{3}4$ , ili češće ${\mathit {d}}={\frac {\log 4}{\log 3}}$ . Prema tome, mjerna jedinica za Kochovu krivulju bi bila otprilike m^1.2619. Općenito, fraktalna dimenzija potpuno samosličnog fraktala računa se po formuli ${\mathit {d}}={\frac {\log {\mathit {N}}}{\log {\mathit {L}}}}$ .

Minkowski-Bouligandova dimenzija

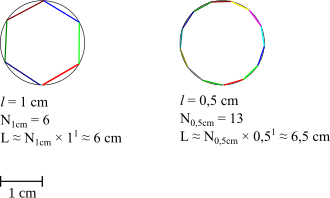
Odnos broja segmenata i duljina njihovih stranica

Uzmimo fraktal koji leži u ravnini i prekrijmo ga proizvoljnim brojem M sukladnih kvadrata duljine stranice A. Smanjivanjem duljine kvadratâ (a time i povećavanjem njihova broja) mijenja se i broj kvadrata koji sadrže fraktal. Ova metoda koristi odnos broja tih kvadrata i duljine stranica. Pokušajmo tako odrediti dimenziju jednostavnih objekata, čija nam je dimenzija već poznata (razne definicije dimenzije ne bi trebale davati različite rezultate kod vrlo jednostavnih objekata), npr. kvadrata. Odnos broja kvadrata i duljina stranice možemo vidjeti na slici desno. Dobivamo opću formulu za kvadrat (za koji znamo da je dvodimenzionalan): ${\mathit {M}}={\frac {1}{{\mathit {A}}^{2}}}$ . Ako učinimo istu stvar s dužinom (jednodimenzionalnom) i kockom (trodimenzionalnom), vidimo opće formule ${\mathit {M}}={\frac {1}{\mathit {A}}}$ i ${\mathit {M}}={\frac {1}{{\mathit {A}}^{3}}}$ . Iz ova tri primjera vidimo opću formulu za objekte bilo koje dimenzije: ${\mathit {M}}={\frac {1}{{\mathit {A}}^{\mathit {d}}}}$ , odnosno ${\mathit {d}}={\frac {\log {\mathit {M}}}{\log {\frac {1}{\mathit {A}}}}}$ . Treba napomenuti da ova metoda ne daje potpuno točne rezultate, te da joj se rezultati primiču stvarnima s povećanjem broja dužina, kvadrata, kocaka... Koristi se kod određivanja fraktalne dimenzije nepravilnih objekata, npr. bifurkacijskog dijagrama populacijske jednadžbe.

Vidi još