Električna rezonancija

Elektromagnetizam

Elektricitet • Magnetizam Elektrostatika Električni naboj • Coulombov zakon • Električno polje • Električni tok • Gaussov zakon • Električni potencijal • Elektrostatska indukcija • Električni dipolni moment • Gustoća polarizacije Magnetostatika Ampèreov zakon • Električna struja • Magnetsko polje • Magnetizacija • Magnetski tok • Biot–Savartov zakon • Magnetski dipolni moment • Gaussov zakon za magnetizam Elektrodinamika Zrakoprazan prostor • Lorentzov zakon • ems • Elektromagnetska indukcija • Faradayev zakon • Lenzov zakon • Struja pomaka • Maxwellove jednadžbe • EM polje • Elektromagnetsko zračenje • Liénard-Wiechertov potencijal • Maxwellov tenzor • Vrtložne struje Električna mreža Električna vodljivost • Električni otpor • Električni kapacitet • Električni induktivitet • Impedancija • Rezonantne šupljine • Vodiči valova Kovarijantna formulacija Elektromagnetski tenzor • EM Stres-energijski tenzor • Četvero-struja • Elektromagnetski četvero-potencijal Znanstvenici Ampère • Coulomb • Faraday • Gauss • Heaviside • Henry • Hertz • Lorentz • Maxwell • Tesla • Volta • Weber • Ørsted

Električni rezonantni sustav može biti predočen, na primjer, serijskim titrajnim krugom sastavljenim od idealnog induktiviteta L i idealnog kapaciteta C, gdje titrajni krug ne sadrži radne otpore koji bi uzrokovali gubitke energije. Pobudimo li takav titrajni krug na titranje, strujnim krugom će poteći struja kao odziv titrajnog kruga na pobudu.

Titrajni krug ili LC krug (lijevo) se sastoji od električne zavojnice s feritnom (feromagnetskom) jezgrom i električnog kondenzatora, a koristi se za radio sat.

Električna rezonancija je pojava pri kojoj za određenu frekvenciju u električnom titrajnom krugu nastupa titranje s ekstremno velikom ili ekstremno malom strujnom amplitudom. Pojam rezonancije povezan je s porastom jakosti (intenziteta) titraja kada se učestalost vanjske sile, koja uzrokuje titraje, podudara s učestalošću rezonantne frekvencije sustava. Tijekom tog procesa dolazi najčešće do naizmjenične pretvorbe jednog oblika energije u drugi, kao na primjer kinetičke u potencijalnu ili energije električnog polja u energiju magnetskog polja. Pojave vezane za rezonanciju mogu se uočiti u brojnim fizikalnim sustavima, no u elektrotehnici je posebno zanimljiva pojava rezonancije u električnim titrajnim krugovima koja ima mnogobrojne primjene.

Objašnjenje

Priključimo u seriju na gradsku mrežu izmjenične struje električnu žarulju, električnu zavojnicu i električni kondenzator. Neka zavojnica ima otvorenu željeznu jezgru koju možemo zatvoriti kotvom. Kad je željezna jezgra otvorena, žarulja slabo svijetli. Međutim, kad željeznu jezgru počnemo zatvarati, žarulja će svijetliti sve jače do nekog najvećeg sjaja, pa će kod konačnog zatvaranja jezgre opet slabo svijetli. Tu pojavu tumačimo na sljedeći način. Pri zatvaranju jezgre mijenjao se induktivitet zavojnice, a prema tome i frekvencija našeg titrajnog kruga. Kad je frekvencija titrajnog kruga postala jednaka frekvenciji gradske mreže, nastala je električna rezonancija. Već nam je, naime, otprije poznato da induktivitet i kapacitet stvaraju izmjeničnoj struji izvjestan električni otpor koji ovisi o frekvenciji te struje. Što je frekvencija veća, to je induktivni otpor veći, a kapacitivni otpor manji. Serijskim spajanjem kondenzatora i zavojnice u oscilatornom krugu, djelovanja njihovih otpora su suprotna. Za izvjesnu vrijednost L i C u titrajnom krugu ti će otpori biti jednaki, a jer djeluju u suprotnom smjeru, oni će se poništavati. Ovi otpori kao da više ne postoje, već ostaje samo omski otpor titrajnog kruga. Frekvencija kod koje je kapacitivni otpor jednak induktivnom otporu zove se rezonantna frekvencija ili vlastita frekvencija titrajnog kruga. Kaže se da je oscilatorni krug u rezonanciji za određenu frekvenciju, pa je jakost struje u tom slučaju najveća. Tako je bilo i kod našeg pokusa, te je u času rezonancije žarulja najjače zasvijetlila.

Iz uvjeta rezonancije da je induktivni otpor jednak kapacitivnom izvodimo Thomsonov izraz za rezonantnu frekvenciju titrajnog kruga, to jest:

$L\cdot \omega ={\frac {1}{C\cdot \omega }}$

pa je:

$\omega ^{2}={\frac {1}{L\cdot C}}$

kako je:

$\omega =2\cdot \pi \cdot f$

to je:

$f={\frac {1}{2\cdot \pi \cdot {\sqrt {L\cdot C}}}}$

U tom izrazu je L izraženo u henrijima, a C u faradima, pa se f dobije u hercima.

Kako je:

$\omega ={\frac {2\cdot \pi }{T}}$

to je period električnih oscilacija:

$T=2\cdot \pi \cdot {\sqrt {L\cdot C}}$

Električni titrajni krugovi

Podrobniji članak o temi: Titrajni krug

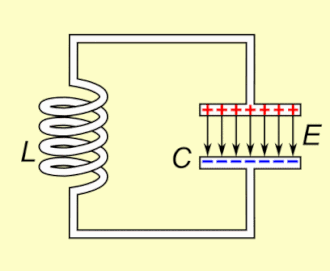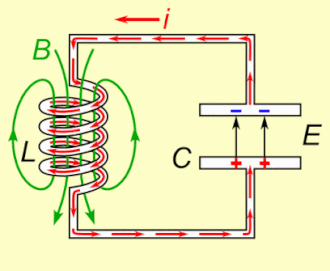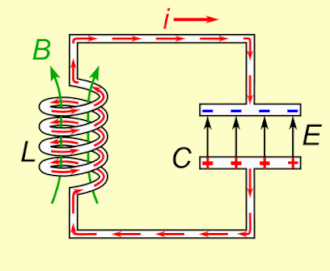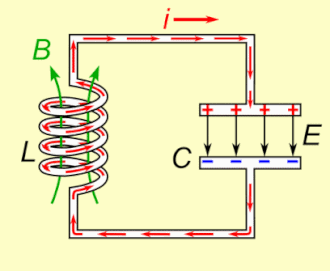
Najjednostavniji titrajni električni sustav sastoji se od električne zavojnice i električnog kondezatora s odgovarajućim nazivnim induktivitetom, odnosno električnim kapacitetom (u daljnjem tekstu skraćeno: zavojnica, kondenzator, induktivitet, kapacitet, struja, napon i tako dalje). Pobuđeni impulsom iz odgovarajućeg električnog izvora, titrajni krug će zatitrati na način da će energija određenom učestalošću naizmjence prelaziti sa zavojnice na kondenzator i natrag na zavojnicu. Tijekom tog procesa dolazi do naizmjenične pretvorbe energije magnetskog polja u zavojnici u energiju električnog polja u kondenzatoru i natrag u energiju magnetskog polja u zavojnici. Energija prelazi u obliku izmjenične električne struje periodičkog sinusoidalnog oblika i to one frekvencije koja je određena rezonantnim svojstvima titrajnog kruga. Ukoliko takav titrajni krug ne bi sadržavao otpore koji bi uzrokovali gubitke energije, takvo neprigušeno titranje bi trajalo praktički neograničeno dugo i to odgovarajućom rezonantnom kružnom frekvencijom $\omega \,$ koja je određena induktivitetom zavojnice i kapacitetom kondenzatora:

$\omega =2\cdot \pi \cdot f={\sqrt {\frac {1}{L\cdot C}}}$

Međutim, ukoliko je u titrajnom krugu prisutan i jedan ili više otpora, titrajni krug će zatitrati na nešto nižoj frekvenciji uz eksponencijalno prigušenje koje u nekom datom titrajnom krugu ovisi o rezultantnom otporu koji prouzrokuje energetske gubitke.

Rezonancija u električnim titrajnim krugovima

Električni rezonantni sustavi imaju svojstvo da im u frekvencijskom području rezonancije električna impedancija poprima ekstremne vrijednosti što ima i odgovarajući utjecaj na veličinu električne struje u strujnom krugu kao odziva na vanjsku pobudu. Električna impedancija serijskog titrajnog kruga bi u idealnim uvjetima na rezonantnoj frekvenciji postala jednaka nuli, a električna impedancija paralelnog titrajnog kruga u istim uvjetima beskonačno velika. Međutim, u stvarnim uvjetima je postizanje ekstrema ograničeno rezultantnim otporom gubitaka u titrajnom krugu (radni otpor zavojnice, odn. otpor izolacije kondenzatora).

Električna rezonancija u serijskom titrajnom krugu

Električna rezonancija u serijskom titrajnom krugu opaža se porastom, odn. povećanjem amplitude odziva (jakosti električne struje) na vanjsku pobudu (priključeni izmjenični električni napon). U tom smislu je u području rezonancije impedancija, a time i struja, određena praktički samo nadomjestnim radnim otporom koji je uzrokom energetskih gubitaka u krugu:

$I(j\omega \,)={\frac {U(j\omega \,)}{Z(j\omega \,)}}={\frac {U(j\omega \,)}{R_{s}+j(\omega \,L-{\frac {1}{\omega \,C}})}}\,$

gdje su I, U i Z električna struja, napon i impedancija kao funkcije kružne frekvencije, Rs nadomjestni otpor gubitaka u serijskom spoju, L induktivitet zavojnice i C kapacitet kondenzatora u titrajnom krugu. Za frekvencije niže od rezonantne, serijski titrajni krug predstavlja kapacitivno opterećenje, za frekvencije više od rezonantne induktivno opterećenje, a na samoj rezonantnoj frekvenciji radno opterećenje.

Apsolutna vrijednost impedancije serijskog titrajnog kruga je određena kao

$|{Z}|={\sqrt {{Z}{Z}^{*}}}={\sqrt {R_{s}^{2}+(\omega \,L-{\frac {1}{\omega \,C}})^{2}}}$

a fazni kut sa

$\varphi =\arctan {\left({\frac {\omega \,L-{\frac {1}{\omega \,C}}}{R_{s}}}\right)}$

Električna rezonancija u paralelnom titrajnom krugu

Električna rezonancija u paralelnom titrajnom krugu opaža se padom, odn. smanjenjem amplitude odziva (jakosti struje) na vanjsku pobudu (priključeni izmjenični napon). U tom smislu je u području rezonancije admitancija, a time i struja, određena praktički samo nadomjestnim radnim otporom koji je uzrokom energetskih gubitaka u krugu:

$I(j\omega \,)=U(j\omega \,)Y(j\omega \,)=U(j\omega \,)({\frac {1}{R_{p}}}+j(\omega \,C-{\frac {1}{\omega \,L}}))\,$

gdje su I, U i Y električna struja, napon i admitancija kao funkcije kružne frekvencije, Rp nadomjestni otpor gubitaka u paralelnom spoju, L induktivitet zavojnice i C kapacitet kondenzatora u titrajnom krugu. Za frekvencije niže od rezonantne, paralelni titrajni krug predstavlja induktivno opterećenje, za frekvencije više od rezonantne kapacitivno opterećenje, a na samoj rezonantnoj frekvenciji radno opterećenje.

Apsolutna vrijednost admitancije serijskog titrajnog kruga je određena kao

$|{Y}|={\sqrt {{Y}{Y}^{*}}}={\sqrt {{\frac {1}{R_{p}^{2}}}+(\omega \,C-{\frac {1}{\omega \,L}})^{2}}}$

a fazni kut sa

$\varphi =\arctan {\left({\frac {\omega \,C-{\frac {1}{\omega \,L}}}{R_{p}}}\right)}$

Pojmovi i veličine u vezi s rezonancijom

Titrajni krugovi definirani su primarno nazivnim vrijednostima induktiviteta zavojnice i kapaciteta kondenzatora, rezonantnom frekvencijom te rezultantnim otporom koji je uzrokom energetskih gubitaka u titrajnom krugu. Za detaljnije razmatranje titrajnih krugova definira se i širina prijenosnog frekvencijskog pojasa s amplitudnim padom od – 3 dB na donjem i gornjem rubu prijenosnog područja kao

$\vartriangle f={\frac {f_{0}}{Q}},$

gdje je Q čimbenik, odn. faktor kvalitete titrajnog kruga, a $f_{0}$ rezonantna frekvencija titrajnog kruga. U serijskom RLC titrajnom krugu faktor kvalitete titrajnog kruga je određen sa:

$Q={\frac {1}{R_{s}}}{\sqrt {\frac {L}{C}}},$

a u paralelnom RLC titrajnom krugu kao:

$Q=R_{p}{\sqrt {\frac {C}{L}}}$

Izvori

1. Frederick Emmons Terman (1932). Radio Engineering. McGraw-Hill Book
2. William McC. Siebert (1986). Circuits, signals, and systems. MIT Press. p. 113. ISBN 9780262192293.
3. Michael H. Tooley (2006). Electronic circuits: fundamentals and applications. ISBN 9780750669238