Pi (broj): razlika između inačica
Bot: Automatski unos stranica |
m Bot: Automatska zamjena teksta (-{{cite book +{{Citiranje knjige) |
||
| Redak 80: | Redak 80: | ||
:<math>\frac{1}{1^2} + \frac{1}{2^2} + \frac{1}{3^2} + \frac{1}{4^2} + \frac{1}{5^2} + \dots = \frac{\pi^2}{6}</math> | :<math>\frac{1}{1^2} + \frac{1}{2^2} + \frac{1}{3^2} + \frac{1}{4^2} + \frac{1}{5^2} + \dots = \frac{\pi^2}{6}</math> | ||
Jednu relativno jednostavnu metodu koja koristi nizove otkrili su [[Gottfried Leibniz]] i [[James Gregory]]<ref>{{ | Jednu relativno jednostavnu metodu koja koristi nizove otkrili su [[Gottfried Leibniz]] i [[James Gregory]]<ref>{{Citiranje knjige |first=Pierre |last=Eymard |coauthors=Jean-Pierre Lafon |others=Stephen S. Wilson (translator)|title=The Number π|url=http://books.google.com/books?id=qZcCSskdtwcC&pg=PA53&dq=leibniz+pi&ei=uFsuR5fOAZTY7QLqouDpCQ&sig=k8VlN5VTxcX9a6Ewc71OCGe_5jk |accessdate=2007-11-04 |year=2004 |month=02 |publisher=American Mathematical Society |language=English |isbn=0821832468 |pages=53 |chapter=2.6 }}</ref>: | ||
:<math>\pi = \frac{4}{1}-\frac{4}{3}+\frac{4}{5}-\frac{4}{7}+\frac{4}{9}-\frac{4}{11}\cdots\! </math>. | :<math>\pi = \frac{4}{1}-\frac{4}{3}+\frac{4}{5}-\frac{4}{7}+\frac{4}{9}-\frac{4}{11}\cdots\! </math>. | ||
| Redak 88: | Redak 88: | ||
{{glavni|Numeričke aproksimacije broja π}} | {{glavni|Numeričke aproksimacije broja π}} | ||
Povijest spoznaja o broju π teče usporedno s razvojem same matematike.<ref>{{ | Povijest spoznaja o broju π teče usporedno s razvojem same matematike.<ref>{{Citiranje knjige |last=Beckmann |first=Petr |authorlink=Petr Beckmann |title=A History of π |year=1976 |publisher=[[St. Martin's Press|St. Martin's Griffin]] |isbn=0-312-38185-9}}</ref> Neki autori napredak na tom polju dijele na tri razdoblja: antičko-u kojem je računat geometrijski, klasično- kojem se računalo pomoću više matematike u Europi oko [[17. stoljeće|17. stoljeća]] te na treće razdoblje-razdoblje digitalnog računanja na računalima.<ref>{{citiranje www|url=http://numbers.computation.free.fr/Constants/Pi/pi.html|naslov=Archimedes' constant π|preuzeto=2007-11-04}}</ref> | ||
=== Geometrijsko razdoblje === | === Geometrijsko razdoblje === | ||
| Redak 123: | Redak 123: | ||
Rekord je [[1424.]] godine potukao perzijski astronom [[Jamshīd al-Kāshī]], koji je izračunao 16 decimala broja π. | Rekord je [[1424.]] godine potukao perzijski astronom [[Jamshīd al-Kāshī]], koji je izračunao 16 decimala broja π. | ||
Prvi veliki napredak u izračunu broja π nakon Arhimeda je napravio njemački matematičar [[Ludolph van Ceulen]] (1540.–1610.), koji je rabio Arhimedovu metodu te pomoću mnogokuta sa 60·20<sup>29</sup> stranica kako bi izračunao 35 decimala broja π. Bio je tako ponosan na izračun, koji je zahtijevao veći dio njegovog života, da je znamenke dao uklesati na svoj nadgrobni spomenik.<ref>{{ | Prvi veliki napredak u izračunu broja π nakon Arhimeda je napravio njemački matematičar [[Ludolph van Ceulen]] (1540.–1610.), koji je rabio Arhimedovu metodu te pomoću mnogokuta sa 60·20<sup>29</sup> stranica kako bi izračunao 35 decimala broja π. Bio je tako ponosan na izračun, koji je zahtijevao veći dio njegovog života, da je znamenke dao uklesati na svoj nadgrobni spomenik.<ref>{{Citiranje knjige | title = Mathematical Tables; Containing the Common, Hyperbolic, and Logistic Logarithms... | author = Charles Hutton | publisher = London: Rivington | year = 1811 | pages = p.13 | url = http://books.google.com/books?id=zDMAAAAAQAAJ&pg=PA13&dq=snell+descartes+date:0-1837&lr=&as_brr=1&ei=rqPgR7yeNqiwtAPDvNEV }}</ref><ref>Isakovič Glaizer, Gerš, ''Povijest matematike za školu'', Školske novine & HMD, Zagreb, 2003., {{ISBN|953-160-176-3}}, str. 210.</ref> | ||
Otprilike u isto doba, metode više matematike i određivanje beskonačnih nizova počele su izranjati po Europi. Prva od poznatih takve vrste je [[Vièteova formula]], | Otprilike u isto doba, metode više matematike i određivanje beskonačnih nizova počele su izranjati po Europi. Prva od poznatih takve vrste je [[Vièteova formula]], | ||
| Redak 181: | Redak 181: | ||
:<math>\pi \approx \frac{(a_n + b_n)^2}{4 t_n}\!</math>. | :<math>\pi \approx \frac{(a_n + b_n)^2}{4 t_n}\!</math>. | ||
Using this scheme, 25 iterations suffice to reach 45 million correct decimals. A similar algorithm that quadruples the accuracy in each step has been found by [[Jonathan Borwein|Jonathan]] and [[Peter Borwein]].<ref>{{ | Using this scheme, 25 iterations suffice to reach 45 million correct decimals. A similar algorithm that quadruples the accuracy in each step has been found by [[Jonathan Borwein|Jonathan]] and [[Peter Borwein]].<ref>{{Citiranje knjige|first=Jonathan M|last=Borwein|authorlink=Jonathan Borwein|coauthors=Borwein, Peter, Berggren, Lennart|date=2004|title=Pi: A Source Book|publisher=Springer|isbn=0387205713}}</ref> The methods have been used by [[Yasumasa Kanada]] and team to set most of the π calculation records since 1980, up to a calculation of 206,158,430,000 decimals of π in 1999. The current record is 1,241,100,000,000 decimals, set by Kanada and team in 2002. Although most of Kanada's previous records were set using the Brent-Salamin algorithm, the 2002 calculation made use of two Machin-like formulas that were slower but crucially reduced memory consumption. The calculation was performed on a 64-node Hitachi supercomputer with 1 [[terabyte]] of main memory, capable of carrying out 2 trillion operations per second. | ||
An important recent development was the [[Bailey-Borwein-Plouffe formula]] (BBP formula), discovered by [[Simon Plouffe]] and named after the authors of the paper in which the formula was first published, [[David H. Bailey]], [[Peter Borwein]], and Plouffe.<ref name="bbpf">{{cite journal | An important recent development was the [[Bailey-Borwein-Plouffe formula]] (BBP formula), discovered by [[Simon Plouffe]] and named after the authors of the paper in which the formula was first published, [[David H. Bailey]], [[Peter Borwein]], and Plouffe.<ref name="bbpf">{{cite journal | ||
Posljednja izmjena od 17. studeni 2021. u 23:10
| Popis brojeva – Iracionalni brojevi s ζ(3) – √2 – √3 – √5 – φ – α – e – π – δ | |
| Binarno | 11,00100100001111110110… |
| Dekadski | 3,14159265358979323846… |
| Heksadekadski | 3,243F6A8885A308D31319… |
| Beskonačni razlomak | Primijeti da niz razlomaka nije periodičan. |
Pi ili π je matematička konstanta, danas široko primjenjivana u matematici i fizici. Definira se kao odnos opsega i promjera kruga. Pi je također poznat i kao Arhimedova konstanta (ne treba ga miješati s Arhimedovim brojem) ili Ludolfov broj. U praksi se bilježi malim grčkim slovom π a u hrvatskom jeziku je pravilno pisati i pi.
Numerička vrijednost pi zaokružena na 64 decimalna mjesta je:
- π ≈ 3,14159 26535 89793 23846 26433 83279 50288 41971 69399 37510 58209 74944 5923
Neke formule u kojima se pojavljuje pi (π)
| Geometrijski oblik | Formula |
|---|---|
| Opseg kruga polumjerа r odnosno promjerа d | |
| Površinа kruga polumjerа r | |
| Površinа elipse sa poluosima a i b | |
| Obujam kugle polumjerа r | |
| Površinа kugle polumjerа r | |
| Obujam valjka visine H i polumjerа r | |
| Površina valjka visinе H i polumjerа r | |
| Obujam stošca visinе H i polumjerа r | |
| Površinа stošca visine H i polumjerа r |
Osnove
Definicija
Broj π se definira kao omjer opsega i promjera kružnice.
Primijetite da omjer O/d ne ovisi o veličini kruga.
Druga pak definicija proizlazi iz površine kruga. Pi je omjer površine kruga i kvadrata radijusa:
Iracionalnost
Konstanta π je iracionalan broj koji se ne može definirati omjerom dva cijela broja. To je 1761. godine dokazao Johann Heinrich Lambert. Dokazi izvedeni u 20. stoljeću vrlo često zahtijevaju znanje integralnog računa i visoke matematike općenito.
Računanje broja π
π se može empirijski procijeniti crtanjem velikog kruga, zatim mjerenjem njegovog promjera i opsega te dijeljenjem opsega promjerom. Drugo geometrijski zasnovano približenje po Arhimedu[1], računanje opsega, Pn, pravilnog mnogokuta sa n stranica upisanih u kružnicu promjera d. Tako se dobije
Postoje i čisto numeričke metode za računanje π. No, u većini slučajeva one su posve nedokučive geometrijskoj intuiciji jer koriste razne jednakosti koje povezuju algebru, trigonometriju i druga područja matematike, a u kojima se (katkada neočekivano) pojavljuje π. Primjer je suma niza recipročnih kvadrata prirodnih brojeva - tzv. Baselski problem, čije je rješenje Euleru dalo motivaciju za Riemannovu zeta-funkciju:[2]
Jednu relativno jednostavnu metodu koja koristi nizove otkrili su Gottfried Leibniz i James Gregory[3]:
- .
Navedeni niz je lagan za izračun, no nije odmah uočljivo da je rezultat π. Štoviše, ovaj niz konvergira tako sporo da je nužno preko 300 članova kako bi se dobile točne 2 decimale [4].
Povijest
Povijest spoznaja o broju π teče usporedno s razvojem same matematike.[5] Neki autori napredak na tom polju dijele na tri razdoblja: antičko-u kojem je računat geometrijski, klasično- kojem se računalo pomoću više matematike u Europi oko 17. stoljeća te na treće razdoblje-razdoblje digitalnog računanja na računalima.[6]
Geometrijsko razdoblje
Činjenica da je omjer opsega kružnice i promjera isti za sve kružnice te da iznosi malo više od 3 bila je poznata i u antičkim vremenima. Tu su činjenicu znali egipatski, babilonski, indijski i grčki matematičari. Najranija poznata aproksimacija datira oko 1900. prije Krista. Ona iznosi 25/8 (Babilon) te 256/81 (Egipat), obe unutar 1 % odstupanja o stvarne vrijednosti.[7] Indijski tekst Shatapatha Brahmana definira vrijednost π kao 339/108 ≈ 3,139. Tanah predlaže u Knjizi o kraljevima da je π = 3. Ta je vrijednost uočljivo netočnija od približenja dostupnih iz tog vremena (600. prije Krista).[8][9]
Arhimed sa Sirakuze (287.-212. pr. Kr.) je bio prvi koji je točno procijenio vrijednost broja π. Shvatio je kako njegova vrijednost može biti određena upisivanjem pravilnih mnogokuta unutar kruga.
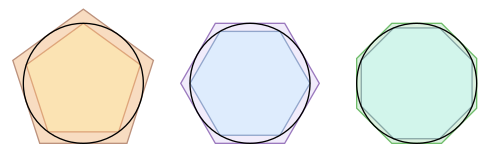
Kako bi izračun bio što točniji trebalo je rabiti mnogokut sa što više kuteva. Koristeći se 96-stranim mnogokutom dokazao je da je 223/71 < π < 22/7.[9]
U sljedećim stoljećima, najveći napredak na tom polju ostvaren je u Indiji i Kini. Oko 265. godine matematičar Liu Hui iz kraljevstva Wei otkrio je jednostavan i točan algoritam za izračun broja pi do bilo koje razine točnosti. On je računao s mnogokutom od 3072 stranice i dobio rezultat pi=3,1416.
Kasnije je Liu Hui izmislio Liu Huijev π algoritam te postigao π=3,1416 koristeći mnogokut od samo 96 stranica, rabeći prednost činjenice da razlika u površinama uzastopnih poligona tvori geometrijski niz s faktorom 4.
Oko 480. godine kineski matematičar Zu Chongzhi dao je aproksimaciju π=355/113 te pokazao da je 3,1415926 < π < 3,1415927. To je dobio rabeći Liu Huijev π algoritam za poligon od 12288 stranica. To će se pokazati najtočnijim izračunom broja u sljedećih 900 godina.
Klasično razdoblje
Do drugog tisućljeća π je bio poznat na manje od 10 decimalnih mjesta. Sljedeći glavni napredak dogodio se pojavom više matematike te posebice otkrićem beskonačnih nizova. Ti nizovi teoretski dopuštaju izračun π do bilo koje željene vrijednosti dodavanjem potrebnog broja članova. Oko godine 1400-te, Madhava iz Sangamagrama je otkrio prvi poznati niz takve vrste:
Ne toliko poznata kao Gregory-Leibnizova formula:
Madhava je uspio izračunati do sljedeće točnosti na 11 decimalnih mjesta:
- π = 3,14159265359 .
Rekord je 1424. godine potukao perzijski astronom Jamshīd al-Kāshī, koji je izračunao 16 decimala broja π.
Prvi veliki napredak u izračunu broja π nakon Arhimeda je napravio njemački matematičar Ludolph van Ceulen (1540.–1610.), koji je rabio Arhimedovu metodu te pomoću mnogokuta sa 60·2029 stranica kako bi izračunao 35 decimala broja π. Bio je tako ponosan na izračun, koji je zahtijevao veći dio njegovog života, da je znamenke dao uklesati na svoj nadgrobni spomenik.[10][11]
Otprilike u isto doba, metode više matematike i određivanje beskonačnih nizova počele su izranjati po Europi. Prva od poznatih takve vrste je Vièteova formula,
koju je otkrio François Viète godine 1593. Drugi poznati rezultat je Wallisov umnožak,
kojega je otkrio John Wallis. Godine 1655. Isaac Newton je osobno izveo niz za računanje π s kojim je izračunao 15 decimala, iako je kasnije priznao: "Sram me reći vam koliko sam figura rabio za ovaj izračun ne imajući nikakvog drugog posla." [12]
Godine 1706. John Machin je prvi izračunao 100 decimala broja π rabeći formulu:
pritom se koristeći formulom
- .
Formule ove vrste, sada poznate pod nazivom strojne formule, su bile korištene za postavljanje nekoliko uspješnih rekorda i ostale zapamćene kao najbolje poznate metode za računanje u doba računala.
Izračuni digitalnog doba
Pojava digitalnih računala u 20. stoljeću dovodi do postavljanja novih rekord u računanju broja π. Koristeći ENIAC, John von Neumann je izračunao 2037 znamenaka broja π godine 1949.. Za taj izračun mu je bilo potrebno 70 sati. Dodatne tisuće decimalnih mjesta dobivene su u sljedećim desetljećima, s prekretnicom godine 1973. kada je izračunata milijunta znamenka.
Napredak nije bio samo posljedica bržih strojeva nego i novih algoritama. Jedan od najznačajnijih napredaka bilo je otkriće Fourierove transformacije godine 1960. koja računalima omogućuje aritmetički izračun ekstremno velikih brojeva vrlo velikom brzinom.
Početkom 20. stoljeća, indijski matematičar Srinivasa Ramanujan je otkrio mnogo novih formula za računanje broja π, od kojih su neke iznimne po svojoj jednostavnosti i matematičkoj pronicljivosti.[13] Dvije njegove najpoznatije formule su:
te
koje donose 14 znamenki po izračunu.[13] Braća Chudnovsky rabila su ovu formulu prilikom nekoliko rekordnih izračuna π krajem 1980-ih, uključujući prvi izračun preko milijardu znamenaka ikad (sa 1.011,196.691 znamenaka) u 1989. godini. Dotična formula i dalje je izbor za računanje u programima za računanje broja na osobnim računalima, za razliku od superračunala koja se rabe za obaranje suvremenih rekorda.
Pamćenje znamenki
Pifilologija je umijeće pamćenja velikog broja znamenki broja π.[14] Rekord u pamćenju znamenki broja π, prema Guinnessovoj knjizi rekorda, je 70 000 znamenki, koje je 21. ožujka 2015. u Indiji izrecitirao Rajveer Meena. Za pothvat mu je trebalo 9 sati i 27 minuti.[15] Jedna od poznatijih tehnika za pamćenje broja pi je tzv piema (poema + pi), gdje pamtimo stihove, a broj slova u svakoj riječi odgovara znamenci broja pi na tom mjestu.
Napredna svojstva
Uporaba u matematici i znanosti
Izvori
- ↑ Groleau, Rick. Infinite Secrets: Approximating Pi. NOVA, preuzeto 2007-11-04
- ↑ +plus magazine An infinite series of surprises, objavljeno 1. prosinca 2001., pristupljeno 1. listopada 2020. (eng.)
- ↑
• Nepoznat parametar:
others
• Nepoznat parametar:month
• Nepoznat parametar:coauthors
• Parametarchapternije dopušten u klasibook
• Parametaraccessdatenije dopušten u klasibook - ↑ • Parametar
typenije dopušten u klasijournal
• Parametarurlnije dopušten u klasijournal
• Parametarformatnije dopušten u klasijournal
• Parametaraccessdatenije dopušten u klasijournal - ↑
• Nepoznat parametar:
authorlink - ↑ Archimedes' constant π, preuzeto 2007-11-04
- ↑ http://mathforum.org/dr.math/faq/faq.pi.html
- ↑ Aleff, H. Peter. Ancient Creation Stories told by the Numbers: Solomon's Pi. recoveredscience.com, preuzeto 2007-10-30
- ↑ 9,0 9,1 O'Connor, J J. A history of Pi, preuzeto 2007-10-30
- ↑ Charles Hutton (1811) Mathematical Tables; Containing the Common, Hyperbolic, and Logistic Logarithms. http://books.google.com/books?id=zDMAAAAAQAAJ&pg=PA13&dq=snell+descartes+date:0-1837&lr=&as_brr=1&ei=rqPgR7yeNqiwtAPDvNEV.
- ↑ Isakovič Glaizer, Gerš, Povijest matematike za školu, Školske novine & HMD, Zagreb, 2003., ISBN 953-160-176-3, str. 210.
- ↑ The New York Times: Even Mathematicians Can Get Carried Away
- ↑ 13,0 13,1 The constant π: Ramanujan type formulas, preuzeto 2007-11-04
- ↑ Script error: The function "harvard_citation_no_bracket" does not exist.
- ↑ "Most Pi Places Memorized", Guinness World Records.
Datoteka:P math.png
Nedovršeni članak Pi (broj) koji govori o matematici treba dopuniti. Dopunite ga prema pravilima uređivanja Hrvatske internetske enciklopedije.























