Beskonačno guste krivulje: razlika između inačica
Bot: Automatski unos stranica |
m Zamjena teksta - '<!--'''(.*)'''-->' u '' |
||
| Redak 1: | Redak 1: | ||
[[Datoteka:Peanocurve.png|mini|400px|prve tri iteracije [[Peanova krivulja|Peanove krivulje]]]] | |||
'''Beskonačno guste krivulje''' su [[fraktali|fraktalne]] [[krivulje]] koje nakon beskonačnog broja [[iteracija]] potpuno prekrivaju dio n-[[dimenzija|dimenzionalnog]] [[prostor]]a u kojem se nalaze, n > 1. Tako će beskonačno gusta krivulja u [[ravnina|ravnini]] zauzimati svaku [[Točka (geometrija)|točku]] npr. [[kvadrat]]a, a u trodimenzionalnom prostoru svaku točku [[kocka|kocke]]. Prvi ih je opisao [[Italija|talijanski]] [[:Kategorija:Matematičari|matematičar]] [[Giuseppe Peano]] pa se sve one ponekad nazivaju [[Peanova krivulja|Peanovim krivuljama]]. | '''Beskonačno guste krivulje''' su [[fraktali|fraktalne]] [[krivulje]] koje nakon beskonačnog broja [[iteracija]] potpuno prekrivaju dio n-[[dimenzija|dimenzionalnog]] [[prostor]]a u kojem se nalaze, n > 1. Tako će beskonačno gusta krivulja u [[ravnina|ravnini]] zauzimati svaku [[Točka (geometrija)|točku]] npr. [[kvadrat]]a, a u trodimenzionalnom prostoru svaku točku [[kocka|kocke]]. Prvi ih je opisao [[Italija|talijanski]] [[:Kategorija:Matematičari|matematičar]] [[Giuseppe Peano]] pa se sve one ponekad nazivaju [[Peanova krivulja|Peanovim krivuljama]]. | ||
Posljednja izmjena od 26. prosinac 2024. u 02:32
Beskonačno guste krivulje su fraktalne krivulje koje nakon beskonačnog broja iteracija potpuno prekrivaju dio n-dimenzionalnog prostora u kojem se nalaze, n > 1. Tako će beskonačno gusta krivulja u ravnini zauzimati svaku točku npr. kvadrata, a u trodimenzionalnom prostoru svaku točku kocke. Prvi ih je opisao talijanski matematičar Giuseppe Peano pa se sve one ponekad nazivaju Peanovim krivuljama.
Svojstva
Fraktalne dimenzije svih beskonačno gustih krivulja odgovaraju topološkoj dimenziji prostora u kojem se nalaze, baš zato što ispunjavaju cijeli taj prostor, iako je njihova topološka dimenzija uvijek 1. Dakle, fraktalna dimenzija beskonačno gustih krivulja na ravnini (jediničnom kvadratu) je 2, u prostoru (jediničnoj kocki) 3 itd.
Uvod

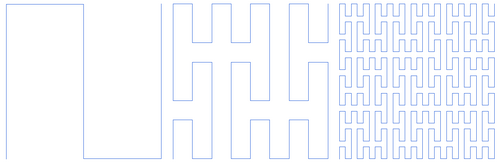
Što znači da krivulja potpuno prekriva kvadrat? U teoriji to znači da ona nakon beskonačnog broja iteracija zauzima svaku točku kvadrata. U praksi se to može shvatiti korištenjem pojma razlučivosti koji označava broj točaka računalnog zaslona (ili slične naprave) koje su potrebne da se nacrta takav kvadrat. Ako nacrtamo sivi kvadrat od n puta n točaka i u njemu krivulju bijele boje te ako nakon njene m-te iteracije svaka od n2 točaka bude bijela, krivulja je beskonačno gusta (vidi sliku Hilbertove krivlje desno).