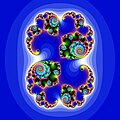
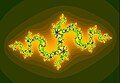
Julijev skup

Julijev skup (u širem smislu) je granica dvaju skupova točaka [math]\displaystyle{ z_0=x+yi }[/math]: onog gdje niz [math]\displaystyle{ \mathit{z}_{n+1} = f(z_n) }[/math] konvergira nekoj vrijednosti te onog gdje taj niz divergira, odnosno teži u beskonačnost ([math]\displaystyle{ f(z_n) }[/math] može biti bilo koja funkcija).

Julijev skup (u užem smislu) dobijemo ako u gorenavedeni niz uvrstimo [math]\displaystyle{ f(z_n)=z_n^2+c }[/math].

Dobio je ime po francuskom matematičaru Gastonu Juliji.

Uvod

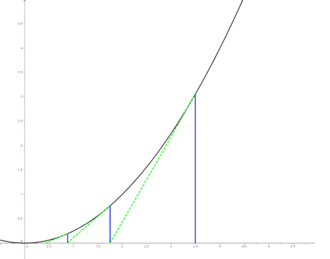
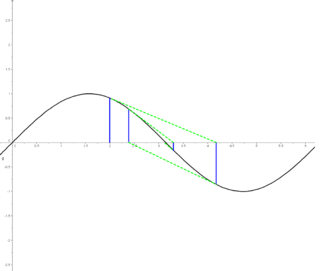
aproksimacija funkcije [math]\displaystyle{ f(x)=\frac{x^2}{4} }[/math]

aproksimacija funkcije [math]\displaystyle{ f(x)=\sin x }[/math]

U 16. stoljeću talijanski su matematičari razvili egzaktne formule za rješavanje algebarskih jednadžba trećeg i četvrtog stupnja, a početkom 19. stoljeća matematičar Niels Abel dokazao je da ne postoje općenite, univerzalne formule, odnosno metode kojima bi se egzaktno rješavale algebarske jednadžbe petog i višeg stupnja. No, takve se jednadžbe mogu rješiti aproksimativno, do potrebne točnosti. Metode aproksimativnog rješavanja jednadžbâ sustavno su se razvijale tijekom više stoljeća. Isaac Newton razvio je specifičnu iteracijsku metodu koju je kasnije usavršio Joseph Raphson.

Graf jednadžbe trećeg stupnja u kompleksnoj ravnini - sve točke iste boje konvergiraju jednom rješenju.

Radi se o aproksimaciji rješenja pomoću tangenata funkcije. Ako znamo da je rješenje neke jednadžbe (nultočka funkcije) u intervalu [a, b] u kojem je funkcija neprekidna, dobit ćemo približno rješenje tako da odaberemo jednu od krajnjih točaka intervala, nađemo vrijednost funkcije u toj točki, povučemo tangentu i označimo njezino sjecište s apscisom. Postupak ponovimo s označenom točkom dok ne postanemo zadovoljni točnošću rješenja. Treba primijetiti da u slučajevima sa slikâ sa strane aproksimativna rješenja postaju sve bliža stvarnom rješenju, odnosno konvergiraju mu, iako su kod lijeve funkcije dva "susjedna" aproksimativna rješenja uvijek sa suprotne strane stvarnog. Općenito za neku funkciju vrijedi da svaka točka skupa [math]\displaystyle{ \mathbb{R} }[/math] konvergira k najbližoj nultočki funkcije. Problem se javlja kod točaka koje su jednako udaljene od dvije nultočke – tada možemo reći da obje nultočke jednakom jačinom "privlače" točku te ona ne konvergira nijednoj, a nazivamo ju divergentnom točkom.

Ako ovu metodu primijenimo na kompleksnu ravninu, sve će biti isto kod funkcija prvog i drugog stupnja. No, za funkcije višeg stupnja stvari nisu toliko jednostavne. Iz grafa sa strane vidimo da su granice tri skupa iznimno složene te da daljnjim uvećavanjem (povećavanjem razlučivosti) dobivamo sve veću složenost. Osim toga, granična područja sadrže područja koja su potpuno slična većim područjima u kojima se nalaze. Drugim riječima, ona sadrže svojstvo samosličnosti. Iz ta dva svojstva možemo zaključiti da su to fraktali.

Konstrukcija

Ako za svaku točku kompleksne ravnine [math]\displaystyle{ z_0=x+yi }[/math] definiramo niz [math]\displaystyle{ \mathit{z}_{n+1} = f(z_n) }[/math], gdje [math]\displaystyle{ f(z_n) }[/math] može biti bilo koja funkcija, možemo definirati dva skupa: skup točaka z₀ za koje definirani niz konvergira nekoj točki i skup točaka z₀ za koje taj niz divergira, odnosno teži u beskonačnost. Julijev skup (u širem smislu) je granica tih dvaju skupova. Obično se Julijev skup, kao i svi algebarski fraktali, prikazuje tako da su točke koje konvergiraju crne, a one koje divergiraju u raznim su nijansama iste ili različitih boja. Nijansa boje ovisi o brzini kojom niz raste – što se više odmičemo od Julijevog skupa, niz brže raste. Mijenjanjem konstante c u Julijevom skupu u užem smislu dobivamo najrazličitije skupove (vidi galeriju pod "Povezanost").

Povezanost

Julijev je skup povezan ako je skup kojeg okružuje kompaktan. Ova je osobina vrlo važna za definiciju Mandelbrotovog skupa.

c=1-φ, φ = zlatni rez
(povezan)
c=(φ-2)+(φ-1)i = -0.4+0.6i
(nepovezan)
c=0.285+0i
(nepovezan)
c=0.285+0.01i
(nepovezan)
c=0.45+0.1428i
(nepovezan)
c=-0.70176-0.3842i
(povezan)
c=-0.835-0.2321i
(povezan)

Vidi još

Na Zajedničkom poslužitelju postoje datoteke na temu: Julijev skup.