Eksponencijalna funkcija

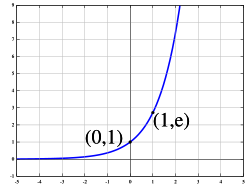
U matematici eksponencijalna funkcija je funkcija f(x) = e^x gdje je broj e prirodna konstanta i baza prirodnih logritama. Funkcija f(x) = e^x je definirana unutar cijelog skupa realnih brojeva, monotono je rastuća porastom nezavisne varijable x, gdje se brzina rasta povećava kako raste x.

Graf funkcije (slika desno) leži iznad x-osi, ali joj se asimptotski približava kako x teži prema sve manjim negativnim vrijednostima. Brzina rasta funkcije je u svakoj točki jednaka vrijednosti funkcije u toj točki. Inverzna funkcija eksponencijalne funkcije je funkcija prirodnog logaritma f(x) = ln(x) te se u starijim izvorima eksponencijalna funkcija spominje kao antilogaritamska funkcija.

Definicija

Eksponencijalna funkcija (plavo) i vrijednost limesa za n=0 do n=8 (crveno).

Eksponencijalna funkcija e^x može biti definirana kao niz potencija razvijenih u Taylorov red:

e^{x}=\sum _{n=0}^{\infty }{x^{n} \over n!}=1+x+{x^{2} \over 2!}+{x^{3} \over 3!}+{x^{4} \over 4!}+\cdots .

Eksponencijalna funkcija se može također izraziti i kao limes:

e^{x}=\lim _{n\rightarrow \infty }\left(1+{\frac {x}{n}}\right)^{n}.

Kako n raste, vrijednost limesa izraza se sve više približava vrijednosti e^x (slika desno).

Jedinstveno svojstvo eksponencijalne funkcije može se izraziti pomoću jednakosti

e^{(x+y)}=e^{x}\cdot e^{y}\,

odnosno napisano drukčije

\exp(x+y)=\exp(x)\cdot \exp(y).

Razvoj funkcije $e^{x}$ preko limesa

Očito za svaki $x\in \mathbb {R}$ kada $n\rightarrow \infty$ vrijedi $e^{\frac {x}{n}}\rightarrow 1.$ Slično se vidi i da $(1+{\frac {x}{n}})\rightarrow 1.$ Za dovoljno veliki $n$ možemo reći da razlika ova dva (pozitivna) broja postaje zanemariva, tj. $e^{\frac {x}{n}}=\lim _{n\to \infty }(1+{\frac {x}{n}})$ pa je zaista $e^{x}=\lim _{n\to \infty }(1+{\frac {x}{n}})^{n}.$

Ovaj je identitet itekako koristan u realnoj analizi pri izučavanja eksponencijalnih, ali i nekih drugih funkcija. Neka imamo primjerice funkciju $f(x)=a^{x},a\in \mathbb {R_{\geq 0}} .$ Tada možemo pisati $f(x)=e^{x\ln _{a}}.$ Ovo je korisno zbog važnog svojstva funkcije $e^{x},$ a to je ${\frac {d}{dx}}e^{x}=e^{x}.$

S druge strane, gore razrađeni identitet je baza kompleksne analize. Defniramo kompleksnu eksponencijalnu funkciju $e^{ix}$ stavljajući $x:=xi,$ gdje je $i^{2}=-1.$ Time se lako dokaže i Eulerova formula.

Derivacija

Važnost eksponencijalne funkcije u matematici i znanosti potječe uglavnom iz svojstava njezine derivacije koja ima svojstvo da je

\,{d \over dx}e^{x}=e^{x}

što znači da je funkcija e^x ujedno i svoja derivacija. Isto takvo svojstvo imaju i funkcija oblika Ke^x gdje je K konstanta.

Za sve funkcije takvih svojstava vrijedi da je:

strmina, odn. nagib grafa funkcije u svakoj točki jednak vrijednosti funkcije u toj točki,
brzina porasta funkcije za vrijednost slobodne varijable x jednaka vrijednosti funkcije u x,
eksponencijalna funkcije rješenje diferencijalne jednadžbe y ′ = y.

Štoviše, i drugi oblici diferencijalnih jednadžbi nalaze rješenje u eksponencijalnim funkcijama uključivši Schrödingerovu jednadžbu, Laplaceovu jednadžbu te jednadžbu jednostavnog harmoničkog gibanja.

Eksponencijalna funkcija s realnim brojem a kao bazom

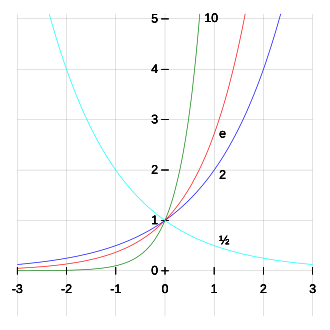
Graf funkcije *f(x)*=a^x za različite baze a: baza10 (zeleno), baza e (crveno), baza 2 (plavo) i baza ½ (cijan). Svaka krivulja prolazi točkom (0,1), a za x=1 vrijednost funkcije je upravo jednaka bazi *f(1)*=a.

Ponekad se pojam eksponencijalne funkcije koristi općenitije za funkcije oblika

f(x)=a^{x}\,

gdje baza a može biti i bilo koji pozitivni realni broj, a ne nužno broj e.

Za eksponencijalne funkcije s drugim bazama vrijedi da je

{d \over dx}a^{x}=(\ln a)a^{x}.

Eksponencijalna funkcija u kompleksnoj ravnini

Eksponencijalna funkcija može se definirati i u kompleksnoj ravnini na nekoliko ravnopravnih načina. Neki od njih odražavaju iste izraze kao i za eksponencijalne funkcije realne varijable. Na primjer, eksponencijalna funkcija kompleksne varijable može se izraziti u obliku reda potencija gdje su realne vrijednosti zamijenjene kompleksnima:

\,\!\,e^{z}=\sum _{n=0}^{\infty }{\frac {z^{n}}{n!}}

Koristeći ovu definiciju jednostavno je pokazati da jednakost

{d \over dz}e^{z}=e^{z}

vrijedi i u kompleksnoj ravnini.

Razmatrana kao funkcija definirana u kompleksnoj ravnini, eksponencijalna funkcija zadržava svoja osnovna svojstva:

\,\!\,e^{z+w}=e^{z}e^{w}

\,\!\,e^{0}=1

\,\!\,e^{z}\neq 0

\,\!\,{d \over dz}e^{z}=e^{z}

za sve kompleksne brojeve z i w. Eksponencijalna funkcija može biti i periodička kada je funkcija imaginarnog argumenta perioda $2\pi i$ jer vrijedi

\,\!\,e^{a+bi}=e^{a}(\cos b+i\sin b)

i

\,e^{z}=e^{x}e^{yi}=e^{x}(\cos y+i\sin y)=e^{x}\cos y+ie^{x}\sin y.

gdje su a i b realne vrijednosti. Jednakost povezuje eksponencijalnu funkciju s trigonometrijskim funkcijama i dalje s hiperboličkim funkcijama. Štoviše, može se definirati i funkcija oblika a^b, gdje su i a i b kompleksne veličine.

Pojam prirodnog logaritma se može također proširiti i na funkciju kompleksnog argumenta ln(z), gdje možemo definirati općenitije da je

\,\!\,z^{w}=e^{w\ln z}

za sve kompleksne brojeve z i w. Ovo je također višeznačna funkcija i identitet vrijedi ukoliko se uzme u obzir višeznačnost funkcije. Naime, upravo zbog višeznačnosti funkcije općenito ne vrijedi pravilo množenja eksponenata za pozitivne realne brojeve

\,\!\,(e^{z})^{w}\neq e^{\left(zw\right)}

Literatura

Gusić J., Mladinić P., Pavković B., "Matematika 2", Školska knjiga, 2006.
Antoliš S., Copić A., "Matematika 4", Školska knjiga, 2006.