Derivacija

Ovo je glavno značenje pojma Derivacija. Za druga značenja pogledajte Derivacija (razdvojba).

Datoteka:Tangency Example 3.svg

Pravac L tangira funkciju f u točki P čija derivacija odgovara nagibu pravca L u točki P

U matematici derivacije funkcija zajedno s integralnim računom glavne su osnove infinitezimalnog računa koji ima široku primjenu u svim znanstvenim i mnogim drugim područjima gdje je potreban proračun razvoja funkcije u određenom intervalu. Tako je npr. u geometriji derivacija nagib tangente na funkciju u određenoj točki, u ekonomiji npr. rast inflacije u vremenu, a u fizici deriviranjem puta po vremenu dobijemo iznos brzine.

Definicija

Ovisno o kontekstu, izraz i smisao definicije derivacije može biti različit. Međutim, u većini primjena u prirodnim, tehničkim i društvenim znanostima, te matematici na razini početnih godina studija, smisao derivacije je sljedeći:

Deriviraju se funkcije. Derivacija opisuje brzinu promjene funkcije u odnosu na promjenu nezavisne varijable (argumenta funkcije). Deriviranjem funkcije dobije se druga funkcija istih argumenata. Za pojedinu vrijednost nezavisne varijable (derivacija u točki), derivacija je u toj točki jednaka 1 ako funkcija raste (povećava se vrijednost funkcije) jednako brzo kao i nezavisna varijabla; ako funkcija raste brže/sporije, derivacija je veća/manja od 1, te jednaka nuli ako se funkcija ne mijenja. Simetrično, ako funkcija pada (umanjuje se vrijednost funkcije dok argument raste), derivacija je negativna. Za neke funkcije derivacija ne postoji u nekim (ili u svim) točkama. Ako derivacija postoji, kaže se da je funkcija derivabilna u tim točkama ili u tome dijelu svoje domene.

Najjednostavnije se definira derivacija realne funkcije jedne realne varijable. Ako je to funkcija f nezavisne varijable označene sa x, tj. funkcija f(x), njezina derivacija u točki x formalno se definira kao:

${\frac {df}{dx}}(x)=f'(x)=Df(x)=\lim _{h\to 0}{\frac {f(x+h)-f(x)}{h}}\,\!$

Na lijevoj strani izraza navedene su tri ekvivalentne oznake za derivaciju funkcije f(x). Derivacija u točki x jednaka je graničnoj vrijednosti ili limesu (oznaka lim) razlomka na desnoj strani.

Sam razlomak je omjer promjene funkcije i promjene nezavisne varijable u blizini proizvoljno odabrane vrijednosti varijable x. Promjena varijable, u nazivniku, obilježena je sa h (često se umjesto h koristi oznaka Δx). Varijabla se, dakle, mijenja sa x na x+h. Pritom se funkcija promijeni sa f(x) na f(x+h), pa njezina promjena iznosi f(x+h)-f(x), kako je navedeno u brojniku.

Vrijednost samog razlomka je prosječna brzina promjene funkcije na intervalu od x do x+h. Ona ovisi o početnoj vrijednosti x i veličini intervala h. Ako se uzastopno uzimaju sve manji i manji intervali h, kod derivabilne funkcije vrijednost razlomka sve se više i više približava broju koji je granična vijednost ili limes razlomka u točki x, odnosno derivacija funkcije u toj točki.

Primjer

Za ilustraciju, ovako se derivira funkcija f(x)=x²:

$(x^{2})'=\lim _{h\rightarrow 0}{\frac {(x+h)^{2}-x^{2}}{h}}=\lim _{h\rightarrow 0}{\frac {2xh+h^{2}}{h}}=\lim _{h\rightarrow 0}(2x+h)=2x$

što znači da je funkcija x² derivabilna u cijeloj domeni (za sve vrijednosti varijable x), a njezina derivacija je funkcija 2x. Derivacija u pojedinoj točki dobije se uvrštavanjem vrijednosti za x, npr. u točki x=3 derivacija funkcije x² iznosi 2x=6.

U gornjem izrazu, prvi razlomak dobiven je upisivanjem funkcije x² umjesto opće oznake f(x) iz definicije derivacije (prethodni izraz). Potom slijedi jednostavni račun u brojniku: kvadriranje binoma u zagradi, te oduzimanje članova x², čime se dobiva drugi razlomak. U narednom koraku pokrati se h (i brojnik i nazivnik podijele se s h), pa se dobije jednostavni izraz 2x+h u zagradi ispred koje je i dalje oznaka "limes h prema nuli".

Jedini konceptualno zanimljiv postupak u opisanome zahvatu je određivanje granične vrijednosti (limesa) promatranih izraza "kada h teži prema nuli". Smisao je sljedeći: za promatrani x (dakle, za proizvoljni broj označen kao x) treba odrediti vrijednost (drugi broj, ovisan o x) kojoj se sve više približava početni razlomak kad se h približava nuli. Prva pomisao mogla bi biti da se odmah naprosto uvrsti h=0 u taj razlomak, ali to ne bi imalo smisla. Naime, h označava promjenu varijable, za koju se računa promjena funkcije; ako je nula, tih promjena nema, pa se iz njih ne može računati brzina promjene funkcije. A i formalno gledano, ne možemo imati nulu u nazivniku, jer je dijeljenje s nulom besmisleno.

Zato provodimo račun kojim se početni razlomak pojednostavnjuje, a oznaka limesa ispred pojedinih izraza govori da h nije jednak nuli, nego ćemo samo promatrati kako se izraz ponaša kad se h približava nuli. Upravo to nam je i omogućilo kraćenje razlomka (dijeljenje s h koje se ne bi moglo provesti ako bi bilo h=0). No, kad dođemo do izraza 2x+h (u zagradi ispred koje još stoji oznaka limesa), postaje napokon očigledno kojoj se vrijednosti taj izraz po volji blizu približava kada h "teži" nuli: ta granična vrijednost je 2x.

Na sličan se način, s malo više računa, određuju derivacije različitih derivabilnih funkcija (neke su navedene u tablici kasnije u tekstu), ili se izvode pravila o deriviranju zbroja funkcija, umnoška itd. Zato se u praktičnom računu opisani postupak više ne mora ponavljati, ako se mogu primjeniti takve "tablične derivacije" i pravila.

O derivacijama višeg reda, parcijalnim derivacijama itd.

Gornja definicija opisuje najjednostavniji pojam derivacije, za koju se još kaže i da je to "obična derivacija prvog reda". Deriviranjem derivacije prvog reda dobiva se derivacija drugog reda iste funkcije. Na sličan način definira se derivacija trećega i viših redova. Za prirodan broj Obrada nije uspjela. (MathML sa SVG ili PNG za rezervu (preporučljivo za moderne preglednike i alate za pristupačnost): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle n} , n-ta derivacija funkcije Obrada nije uspjela. (MathML sa SVG ili PNG za rezervu (preporučljivo za moderne preglednike i alate za pristupačnost): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle f} označava se simbolom

Obrada nije uspjela. (MathML sa SVG ili PNG za rezervu (preporučljivo za moderne preglednike i alate za pristupačnost): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle f^{(n)}(x)}

za Obrada nije uspjela. (MathML sa SVG ili PNG za rezervu (preporučljivo za moderne preglednike i alate za pristupačnost): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle n=0} govori se o nultoj derivaciji koja je neprekidna funkcija Obrada nije uspjela. (MathML sa SVG ili PNG za rezervu (preporučljivo za moderne preglednike i alate za pristupačnost): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle f} .

Ako funkcija ima više nezavisnih varijabli, ona se može derivirati po svakoj varijabli zasebno, smatrajući druge varijable konstantama. Takve se derivacije nazivaju parcijalnim derivacijama. Parcijalno deriviranje drugoga i viših redova može se provoditi po istoj varijabli funkcije, ili po nekoj drugoj od njezinih varijabli (mješovite derivacije).

Parcijalne derivacije se označavaju simbolom Obrada nije uspjela. (MathML sa SVG ili PNG za rezervu (preporučljivo za moderne preglednike i alate za pristupačnost): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \partial} . Tako, na primjer, za funkciju Obrada nije uspjela. (MathML sa SVG ili PNG za rezervu (preporučljivo za moderne preglednike i alate za pristupačnost): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle f} od dvije varijable izraz

Obrada nije uspjela. (MathML sa SVG ili PNG za rezervu (preporučljivo za moderne preglednike i alate za pristupačnost): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{\partial f}{\partial x}}

predstavlja prvu parcijalnu derivaciju. Osim takvih derivacija, za funkcije dviju varijabli može se definirati i derivacija kao polinom Obrada nije uspjela. (MathML sa SVG ili PNG za rezervu (preporučljivo za moderne preglednike i alate za pristupačnost): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle P} :

Obrada nije uspjela. (MathML sa SVG ili PNG za rezervu (preporučljivo za moderne preglednike i alate za pristupačnost): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle P(s, t) = \frac{\partial f}{\partial x}s + \frac{\partial f}{\partial y}t}

Kao i kod realne funkcije realnih varijabli, sličnim graničnim postupkom definiraju se derivacije funkcija kojima su funkcijske vrijednosti ili varijable kompleksni brojevi ili vektori (a često i kada su elementi domene i kodomene neki drugačiji objekti). Pritom se različitim kombinacijama parcijalnih derivacija dobivaju tzv. diferencijalni operatori kao što su gradijent, divergencija itd.

Geometrijska interpretacija

Datoteka:Ableitung.png

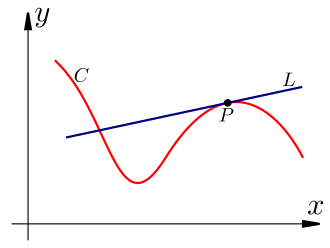
U geometrijskom smislu derivacija funkcije Obrada nije uspjela. (MathML sa SVG ili PNG za rezervu (preporučljivo za moderne preglednike i alate za pristupačnost): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle f} je nagib tangente u određenoj točki Obrada nije uspjela. (MathML sa SVG ili PNG za rezervu (preporučljivo za moderne preglednike i alate za pristupačnost): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle x_0} , odnosno koeficijent smjera pravca koji je tangenta na funkciju Obrada nije uspjela. (MathML sa SVG ili PNG za rezervu (preporučljivo za moderne preglednike i alate za pristupačnost): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle f} u točki čije su koordinate Obrada nije uspjela. (MathML sa SVG ili PNG za rezervu (preporučljivo za moderne preglednike i alate za pristupačnost): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle (x_0,f(x_0))} .

Koeficijent smjera pravca m je:

$m={\frac {y_{2}-y_{1}}{x_{2}-x_{1}}}$

odnosno:

Obrada nije uspjela. (MathML sa SVG ili PNG za rezervu (preporučljivo za moderne preglednike i alate za pristupačnost): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle m =\frac {f(x+h)-f(x)}{(x_0+h)-x_0} =\frac {f(x+h)-f(x)}{h}}

jer je Obrada nije uspjela. (MathML sa SVG ili PNG za rezervu (preporučljivo za moderne preglednike i alate za pristupačnost): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle (x_0+h)-x_0=h} i Obrada nije uspjela. (MathML sa SVG ili PNG za rezervu (preporučljivo za moderne preglednike i alate za pristupačnost): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \Delta x = h} .

Derivacija funkcije je:

Obrada nije uspjela. (MathML sa SVG ili PNG za rezervu (preporučljivo za moderne preglednike i alate za pristupačnost): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle Df =\lim_{h\rightarrow 0}\frac{f(x_0+h)-f(x)}{h}}

Koeficijent smjera pravca usko je povezan sa derivacijom iz razloga što kada interval Obrada nije uspjela. (MathML sa SVG ili PNG za rezervu (preporučljivo za moderne preglednike i alate za pristupačnost): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle x_2-x_1=h} teži nuli, pravac postaje tangenta funkcije, a limes njegovog koeficijenta smjera postaje derivacija funkcije $f$ u točki Obrada nije uspjela. (MathML sa SVG ili PNG za rezervu (preporučljivo za moderne preglednike i alate za pristupačnost): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle (x_0,f(x))} .

Tablica derivacija elementarnih funkcija

Funkcija f(x)	Derivacija Obrada nije uspjela. (MathML sa SVG ili PNG za rezervu (preporučljivo za moderne preglednike i alate za pristupačnost): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle f'(x)}			Funkcija f(x)	Derivacija Obrada nije uspjela. (MathML sa SVG ili PNG za rezervu (preporučljivo za moderne preglednike i alate za pristupačnost): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle f'(x)}
Obrada nije uspjela. (MathML sa SVG ili PNG za rezervu (preporučljivo za moderne preglednike i alate za pristupačnost): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \sin x}	Obrada nije uspjela. (MathML sa SVG ili PNG za rezervu (preporučljivo za moderne preglednike i alate za pristupačnost): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \cos x}			Obrada nije uspjela. (MathML sa SVG ili PNG za rezervu (preporučljivo za moderne preglednike i alate za pristupačnost): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \text{sh}\,x}	Obrada nije uspjela. (MathML sa SVG ili PNG za rezervu (preporučljivo za moderne preglednike i alate za pristupačnost): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \text{ch}\,x}
Obrada nije uspjela. (MathML sa SVG ili PNG za rezervu (preporučljivo za moderne preglednike i alate za pristupačnost): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \cos x}	Obrada nije uspjela. (MathML sa SVG ili PNG za rezervu (preporučljivo za moderne preglednike i alate za pristupačnost): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle -\sin x}			Obrada nije uspjela. (MathML sa SVG ili PNG za rezervu (preporučljivo za moderne preglednike i alate za pristupačnost): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \text{ch}\,x}	${\text{sh}}\,x$
Obrada nije uspjela. (MathML sa SVG ili PNG za rezervu (preporučljivo za moderne preglednike i alate za pristupačnost): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \text{tg}\,x}	Obrada nije uspjela. (MathML sa SVG ili PNG za rezervu (preporučljivo za moderne preglednike i alate za pristupačnost): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{1}{\cos^2 x}}			Obrada nije uspjela. (MathML sa SVG ili PNG za rezervu (preporučljivo za moderne preglednike i alate za pristupačnost): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \text{th}\,x}	${\frac {1}{{\text{ch}}^{2}x}}$
Obrada nije uspjela. (MathML sa SVG ili PNG za rezervu (preporučljivo za moderne preglednike i alate za pristupačnost): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \text{ctg}\,x}	Obrada nije uspjela. (MathML sa SVG ili PNG za rezervu (preporučljivo za moderne preglednike i alate za pristupačnost): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle -\frac{1}{\sin^2 x}}			Obrada nije uspjela. (MathML sa SVG ili PNG za rezervu (preporučljivo za moderne preglednike i alate za pristupačnost): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \text{cth}\,x}	Obrada nije uspjela. (MathML sa SVG ili PNG za rezervu (preporučljivo za moderne preglednike i alate za pristupačnost): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle -\frac{1}{\text{sh}^2 x}}
$\arcsin x$	Obrada nije uspjela. (MathML sa SVG ili PNG za rezervu (preporučljivo za moderne preglednike i alate za pristupačnost): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{1}{\sqrt{1-x^2}}}			Obrada nije uspjela. (MathML sa SVG ili PNG za rezervu (preporučljivo za moderne preglednike i alate za pristupačnost): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \text{Arsh}\,x}	Obrada nije uspjela. (MathML sa SVG ili PNG za rezervu (preporučljivo za moderne preglednike i alate za pristupačnost): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{1}{\sqrt{1+x^2}}}
Obrada nije uspjela. (MathML sa SVG ili PNG za rezervu (preporučljivo za moderne preglednike i alate za pristupačnost): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \arccos x}	$-{\frac {1}{\sqrt {1-x^{2}}}}$			Obrada nije uspjela. (MathML sa SVG ili PNG za rezervu (preporučljivo za moderne preglednike i alate za pristupačnost): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \text{Arch}\,x}	Obrada nije uspjela. (MathML sa SVG ili PNG za rezervu (preporučljivo za moderne preglednike i alate za pristupačnost): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{1}{\sqrt{x^2-1}}}
${\text{arctg}}\,x$	Obrada nije uspjela. (MathML sa SVG ili PNG za rezervu (preporučljivo za moderne preglednike i alate za pristupačnost): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{1}{1+x^2}}			Obrada nije uspjela. (MathML sa SVG ili PNG za rezervu (preporučljivo za moderne preglednike i alate za pristupačnost): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \text{Arth}\,x}	Obrada nije uspjela. (MathML sa SVG ili PNG za rezervu (preporučljivo za moderne preglednike i alate za pristupačnost): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{1}{1-x^2}}
Obrada nije uspjela. (MathML sa SVG ili PNG za rezervu (preporučljivo za moderne preglednike i alate za pristupačnost): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \text{arcctg}\,x }	Obrada nije uspjela. (MathML sa SVG ili PNG za rezervu (preporučljivo za moderne preglednike i alate za pristupačnost): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle -\frac{1}{1+x^2}}			Obrada nije uspjela. (MathML sa SVG ili PNG za rezervu (preporučljivo za moderne preglednike i alate za pristupačnost): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \text{Arcth}\,x}	Obrada nije uspjela. (MathML sa SVG ili PNG za rezervu (preporučljivo za moderne preglednike i alate za pristupačnost): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{1}{1-x^2}}
Obrada nije uspjela. (MathML sa SVG ili PNG za rezervu (preporučljivo za moderne preglednike i alate za pristupačnost): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle e^x}	Obrada nije uspjela. (MathML sa SVG ili PNG za rezervu (preporučljivo za moderne preglednike i alate za pristupačnost): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle e^x}			Obrada nije uspjela. (MathML sa SVG ili PNG za rezervu (preporučljivo za moderne preglednike i alate za pristupačnost): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle a^x}	Obrada nije uspjela. (MathML sa SVG ili PNG za rezervu (preporučljivo za moderne preglednike i alate za pristupačnost): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle a^x \ln a}
$\ln(x)$	Obrada nije uspjela. (MathML sa SVG ili PNG za rezervu (preporučljivo za moderne preglednike i alate za pristupačnost): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{1}{x}}			Obrada nije uspjela. (MathML sa SVG ili PNG za rezervu (preporučljivo za moderne preglednike i alate za pristupačnost): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{1}{x}}	Obrada nije uspjela. (MathML sa SVG ili PNG za rezervu (preporučljivo za moderne preglednike i alate za pristupačnost): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle -\frac{1}{x^2}}
Obrada nije uspjela. (MathML sa SVG ili PNG za rezervu (preporučljivo za moderne preglednike i alate za pristupačnost): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \log_{a} x}	Obrada nije uspjela. (MathML sa SVG ili PNG za rezervu (preporučljivo za moderne preglednike i alate za pristupačnost): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{1}{x \ln a}}			Obrada nije uspjela. (MathML sa SVG ili PNG za rezervu (preporučljivo za moderne preglednike i alate za pristupačnost): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle |x|}	Obrada nije uspjela. (MathML sa SVG ili PNG za rezervu (preporučljivo za moderne preglednike i alate za pristupačnost): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{x}{|x|}}
Obrada nije uspjela. (MathML sa SVG ili PNG za rezervu (preporučljivo za moderne preglednike i alate za pristupačnost): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \sqrt{x}}	Obrada nije uspjela. (MathML sa SVG ili PNG za rezervu (preporučljivo za moderne preglednike i alate za pristupačnost): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{1}{2 \sqrt{x}}}			Obrada nije uspjela. (MathML sa SVG ili PNG za rezervu (preporučljivo za moderne preglednike i alate za pristupačnost): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle x^n}	Obrada nije uspjela. (MathML sa SVG ili PNG za rezervu (preporučljivo za moderne preglednike i alate za pristupačnost): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle n x^{n-1}}

Osnovna pravila deriviranja i izvodi

Ovdje ćemo navesti pravila i dokaze (bez limesa). Ako su funkcije Obrada nije uspjela. (MathML sa SVG ili PNG za rezervu (preporučljivo za moderne preglednike i alate za pristupačnost): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle f, g } diferencijabilne u točki Obrada nije uspjela. (MathML sa SVG ili PNG za rezervu (preporučljivo za moderne preglednike i alate za pristupačnost): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle x } onda možemo derivirati funckije Obrada nije uspjela. (MathML sa SVG ili PNG za rezervu (preporučljivo za moderne preglednike i alate za pristupačnost): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle f \pm g, f \cdot g, \frac{f}{g} } te konačno Obrada nije uspjela. (MathML sa SVG ili PNG za rezervu (preporučljivo za moderne preglednike i alate za pristupačnost): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle f \circ g } u točki Obrada nije uspjela. (MathML sa SVG ili PNG za rezervu (preporučljivo za moderne preglednike i alate za pristupačnost): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle x } .

Derivacija zbroja i razlike

Vrijedi

• Obrada nije uspjela. (MathML sa SVG ili PNG za rezervu (preporučljivo za moderne preglednike i alate za pristupačnost): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \left(f(x)+g(x)\right)'=f'(x)+g'(x)}
• Obrada nije uspjela. (MathML sa SVG ili PNG za rezervu (preporučljivo za moderne preglednike i alate za pristupačnost): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \left(f(x)-g(x)\right)'=f'(x)-g'(x)}

Dokaz. Neka je Obrada nije uspjela. (MathML sa SVG ili PNG za rezervu (preporučljivo za moderne preglednike i alate za pristupačnost): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle h(x) = f(x) + g(x). } Vrijedi Obrada nije uspjela. (MathML sa SVG ili PNG za rezervu (preporučljivo za moderne preglednike i alate za pristupačnost): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle dh = f + df + g + dg - (f + g) = df + dg. } Sada dijeljenjem s Obrada nije uspjela. (MathML sa SVG ili PNG za rezervu (preporučljivo za moderne preglednike i alate za pristupačnost): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle dx } slijedi pravilo. Drugi se slučaj dokazuje analogno, stavljajući Obrada nije uspjela. (MathML sa SVG ili PNG za rezervu (preporučljivo za moderne preglednike i alate za pristupačnost): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle k(x) := - g(x). }

Derivacija umnoška i količnika

• Obrada nije uspjela. (MathML sa SVG ili PNG za rezervu (preporučljivo za moderne preglednike i alate za pristupačnost): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \left(f(x)g(x)\right)'=f'(x)g(x)+f(x)g'(x)}
• Obrada nije uspjela. (MathML sa SVG ili PNG za rezervu (preporučljivo za moderne preglednike i alate za pristupačnost): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \left (\frac{f(x)}{g(x)} \right)'=\frac{f'(x)g(x)-f(x)g'(x)}{g(x)^2}}

Dokaz. Neka je Obrada nije uspjela. (MathML sa SVG ili PNG za rezervu (preporučljivo za moderne preglednike i alate za pristupačnost): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle h(x) = f(x)g(x). } Vrijedi Obrada nije uspjela. (MathML sa SVG ili PNG za rezervu (preporučljivo za moderne preglednike i alate za pristupačnost): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle dh = (f + df)(g + dg) - fg } što daje Obrada nije uspjela. (MathML sa SVG ili PNG za rezervu (preporučljivo za moderne preglednike i alate za pristupačnost): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle fdg + dfg + dfdg. } Sada dijeljenjem s Obrada nije uspjela. (MathML sa SVG ili PNG za rezervu (preporučljivo za moderne preglednike i alate za pristupačnost): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle dx } izraz Obrada nije uspjela. (MathML sa SVG ili PNG za rezervu (preporučljivo za moderne preglednike i alate za pristupačnost): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{dfdg}{dx} } teži u nulu te slijedi pravilo.

Ako su Obrada nije uspjela. (MathML sa SVG ili PNG za rezervu (preporučljivo za moderne preglednike i alate za pristupačnost): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle f, g } obje rastuće i pozitivne može se zamisliti da tražimo stopu promjene površine pravokutnika sa stranicama Obrada nije uspjela. (MathML sa SVG ili PNG za rezervu (preporučljivo za moderne preglednike i alate za pristupačnost): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle f, g.}

Drugi slučaj, odnosno derivacija količnika funkcija Obrada nije uspjela. (MathML sa SVG ili PNG za rezervu (preporučljivo za moderne preglednike i alate za pristupačnost): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle f(x), g(x) } , se dokazuje analogno, stavljajući Obrada nije uspjela. (MathML sa SVG ili PNG za rezervu (preporučljivo za moderne preglednike i alate za pristupačnost): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle h(x) := \frac{1}{g(x)} } i zatim računajući derivaciju funkcije Obrada nije uspjela. (MathML sa SVG ili PNG za rezervu (preporučljivo za moderne preglednike i alate za pristupačnost): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle f(x)h(x)} .

Derivacija složene funkcije (kompozicije)

Vrijedi

• Obrada nije uspjela. (MathML sa SVG ili PNG za rezervu (preporučljivo za moderne preglednike i alate za pristupačnost): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle (f\circ g)'(x)=(f(g(x)))'=f'(g(x)) \cdot g'(x)}

Dokaz. Kada se Obrada nije uspjela. (MathML sa SVG ili PNG za rezervu (preporučljivo za moderne preglednike i alate za pristupačnost): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle x } promijeni na Obrada nije uspjela. (MathML sa SVG ili PNG za rezervu (preporučljivo za moderne preglednike i alate za pristupačnost): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle x + h } to uzrokuje promjenu s Obrada nije uspjela. (MathML sa SVG ili PNG za rezervu (preporučljivo za moderne preglednike i alate za pristupačnost): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle g(x) } na Obrada nije uspjela. (MathML sa SVG ili PNG za rezervu (preporučljivo za moderne preglednike i alate za pristupačnost): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle g(x + h). } Vrijedi Obrada nije uspjela. (MathML sa SVG ili PNG za rezervu (preporučljivo za moderne preglednike i alate za pristupačnost): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle dg = g'(x)dx. } Neovisno o tome vrijedi li Obrada nije uspjela. (MathML sa SVG ili PNG za rezervu (preporučljivo za moderne preglednike i alate za pristupačnost): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle g(x + h) \leq g(x) } ili obrnuto, kada Obrada nije uspjela. (MathML sa SVG ili PNG za rezervu (preporučljivo za moderne preglednike i alate za pristupačnost): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle h \rightarrow 0 } možemo pričati o derivaciji funkcije Obrada nije uspjela. (MathML sa SVG ili PNG za rezervu (preporučljivo za moderne preglednike i alate za pristupačnost): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle f(x) } u Obrada nije uspjela. (MathML sa SVG ili PNG za rezervu (preporučljivo za moderne preglednike i alate za pristupačnost): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle g(x). } Dakle, analogno kao i prije vrijedi Obrada nije uspjela. (MathML sa SVG ili PNG za rezervu (preporučljivo za moderne preglednike i alate za pristupačnost): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle df = f'(g(x)) \cdot dg. } No, vidjeli smo da je Obrada nije uspjela. (MathML sa SVG ili PNG za rezervu (preporučljivo za moderne preglednike i alate za pristupačnost): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle dg = g'(x)dx } odakle slijedi pravilo.

Ulančanost. Ovo se pravilo može objasniti i na sljedeći način. Tražimo stopu promjene izlazne vrijednosti Obrada nije uspjela. (MathML sa SVG ili PNG za rezervu (preporučljivo za moderne preglednike i alate za pristupačnost): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle f } i ulazne vrijednosti Obrada nije uspjela. (MathML sa SVG ili PNG za rezervu (preporučljivo za moderne preglednike i alate za pristupačnost): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle x. } Dakle, Obrada nije uspjela. (MathML sa SVG ili PNG za rezervu (preporučljivo za moderne preglednike i alate za pristupačnost): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle dx } uzrokuje promjenu Obrada nije uspjela. (MathML sa SVG ili PNG za rezervu (preporučljivo za moderne preglednike i alate za pristupačnost): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle dg } koja potom uzrokuje promjenu Obrada nije uspjela. (MathML sa SVG ili PNG za rezervu (preporučljivo za moderne preglednike i alate za pristupačnost): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle df. } Prema tome, vrijedi Obrada nije uspjela. (MathML sa SVG ili PNG za rezervu (preporučljivo za moderne preglednike i alate za pristupačnost): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{df}{dx} = \frac{dg}{dx} \cdot \frac{df}{dg}. }

Lokalna linearizacija. Derivacija kompozicije u točki Obrada nije uspjela. (MathML sa SVG ili PNG za rezervu (preporučljivo za moderne preglednike i alate za pristupačnost): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle x} ima još jedno geometrijsko značenje. Naime, ovo se pravilo vrlo praktično može pokazati linearizirajući stopu izlaznih vrijednosti funkcije Obrada nije uspjela. (MathML sa SVG ili PNG za rezervu (preporučljivo za moderne preglednike i alate za pristupačnost): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle g} lokalno oko točke Obrada nije uspjela. (MathML sa SVG ili PNG za rezervu (preporučljivo za moderne preglednike i alate za pristupačnost): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle x} jer je Obrada nije uspjela. (MathML sa SVG ili PNG za rezervu (preporučljivo za moderne preglednike i alate za pristupačnost): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle g} derivabilna.

Uzmimo na primjer kompoziciju Obrada nije uspjela. (MathML sa SVG ili PNG za rezervu (preporučljivo za moderne preglednike i alate za pristupačnost): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle f(cx)} za, bez smanjenja općenitosti, Obrada nije uspjela. (MathML sa SVG ili PNG za rezervu (preporučljivo za moderne preglednike i alate za pristupačnost): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle c > 1} . Geometrijski možemo shvatiti ovu kompoziciju kao transformaciju skaliranja, u ovom slučaju rastezanja (jer je Obrada nije uspjela. (MathML sa SVG ili PNG za rezervu (preporučljivo za moderne preglednike i alate za pristupačnost): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle c > 1 } ) apscisne osi za faktor Obrada nije uspjela. (MathML sa SVG ili PNG za rezervu (preporučljivo za moderne preglednike i alate za pristupačnost): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle c} .

Rastezanje x-osi za faktor Obrada nije uspjela. (MathML sa SVG ili PNG za rezervu (preporučljivo za moderne preglednike i alate za pristupačnost): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle c} znači da svaki Obrada nije uspjela. (MathML sa SVG ili PNG za rezervu (preporučljivo za moderne preglednike i alate za pristupačnost): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle x_0} na "staroj" x-osi "dovedemo" na mjesto Obrada nije uspjela. (MathML sa SVG ili PNG za rezervu (preporučljivo za moderne preglednike i alate za pristupačnost): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle cx_0} na toj istoj x-osi čime dobivamo novu, rastegnutu x-os. Pritom zamišljamo da je graf, odnosno prikaz njene krivulje, Obrada nije uspjela. (MathML sa SVG ili PNG za rezervu (preporučljivo za moderne preglednike i alate za pristupačnost): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle f(x)} ostao nepromijenjen. Ovo činimo jer je Obrada nije uspjela. (MathML sa SVG ili PNG za rezervu (preporučljivo za moderne preglednike i alate za pristupačnost): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle f(c \cdot \frac{1}{c}x) = f(x)} . (Zbog ovoga je, ako je Obrada nije uspjela. (MathML sa SVG ili PNG za rezervu (preporučljivo za moderne preglednike i alate za pristupačnost): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle f(x)} periodična s temeljnim periodom Obrada nije uspjela. (MathML sa SVG ili PNG za rezervu (preporučljivo za moderne preglednike i alate za pristupačnost): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle P} , funkcija Obrada nije uspjela. (MathML sa SVG ili PNG za rezervu (preporučljivo za moderne preglednike i alate za pristupačnost): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle f(cx)} za Obrada nije uspjela. (MathML sa SVG ili PNG za rezervu (preporučljivo za moderne preglednike i alate za pristupačnost): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle c > 0} također periodična s temeljnim periodom Obrada nije uspjela. (MathML sa SVG ili PNG za rezervu (preporučljivo za moderne preglednike i alate za pristupačnost): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{P}{c}} . Dakle, ako je Obrada nije uspjela. (MathML sa SVG ili PNG za rezervu (preporučljivo za moderne preglednike i alate za pristupačnost): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle 0 < c < 1} temeljni period se povećava, a ako je Obrada nije uspjela. (MathML sa SVG ili PNG za rezervu (preporučljivo za moderne preglednike i alate za pristupačnost): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle c > 1} temeljni se period smanjuje.)

Jasno je da je ovime $\Delta y$ ostao nepromijenjen. No, Obrada nije uspjela. (MathML sa SVG ili PNG za rezervu (preporučljivo za moderne preglednike i alate za pristupačnost): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \Delta x } je postao Obrada nije uspjela. (MathML sa SVG ili PNG za rezervu (preporučljivo za moderne preglednike i alate za pristupačnost): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle c} puta kraći (jer smo x-os rastegnuli za faktor Obrada nije uspjela. (MathML sa SVG ili PNG za rezervu (preporučljivo za moderne preglednike i alate za pristupačnost): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle c} ). Očito je onda nagib Obrada nije uspjela. (MathML sa SVG ili PNG za rezervu (preporučljivo za moderne preglednike i alate za pristupačnost): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{\Delta y}{\Delta x} } postao Obrada nije uspjela. (MathML sa SVG ili PNG za rezervu (preporučljivo za moderne preglednike i alate za pristupačnost): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle c} puta veći.

Na primjer, za Obrada nije uspjela. (MathML sa SVG ili PNG za rezervu (preporučljivo za moderne preglednike i alate za pristupačnost): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle c = 2 } , zamišljamo da smo rastezanjem x-osi brojeve 3, 3.002 doveli na mjesto brojeva 6, 6.004 (ne mijenjajući prikaz krivulje funkcije) pa se razmak između brojeva 6, 6.004 na staroj x-osi promijenio na razmak između brojeva 3, 3.002 na novoj x-osi. Zbog toga je očito razmak postao dvostruko kraći. Nagib je zato u tom slučaju dvostruko veći.

No, to onda znači da je Obrada nije uspjela. (MathML sa SVG ili PNG za rezervu (preporučljivo za moderne preglednike i alate za pristupačnost): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle f(cx)' = f'(cx) \cdot c } .

Ovo se lako može poopćiti.

Naime, kako su Obrada nije uspjela. (MathML sa SVG ili PNG za rezervu (preporučljivo za moderne preglednike i alate za pristupačnost): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle f(x), g(x)} obje derivabilne, slijedi da se u okolini točke Obrada nije uspjela. (MathML sa SVG ili PNG za rezervu (preporučljivo za moderne preglednike i alate za pristupačnost): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle x} , odnosno u intervalu Obrada nije uspjela. (MathML sa SVG ili PNG za rezervu (preporučljivo za moderne preglednike i alate za pristupačnost): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle (x - \Delta x, x + \Delta x)} za Obrada nije uspjela. (MathML sa SVG ili PNG za rezervu (preporučljivo za moderne preglednike i alate za pristupačnost): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \Delta x \rightarrow 0 } funkcija Obrada nije uspjela. (MathML sa SVG ili PNG za rezervu (preporučljivo za moderne preglednike i alate za pristupačnost): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle g(x)} ponaša kao linearna funkcija, čime je pravilo za derivaciju kompozicije dokazano.