Trenje
Trenje je sila kojom se površina na kojoj tijelo miruje ili po kojoj se giba opire gibanju ili otpor sredstva kroz koje se tijelo giba. Trenje je posljedica kemijskog i mehaničkog međudjelovanja tvari u dodiru (tarnog para), to jest ovisi o kemijskom sastavu i hrapavosti dodirnih površina. Razlikuju se trenje mirovanja (statičko trenje) i trenje gibanja (kinematičko trenje), koje može biti trenje klizanja, trenje kotrljanja i otpor fluida gibanju čvrstih tijela (viskoznost). Smjer trenja mirovanja suprotan je smjeru djelovanja zbroja vanjskih sila na tijelo, a smjer trenja gibanja tijela suprotan je smjeru brzine. Mjerna je jedinica trenja njutn (N). [1]
Trenje je sila koja se protivi klizanju jednoga tijela uz drugo dok se tijela međusobno pritišću, a djeluje u području dodira. Kada dođe do takvog klizanja, na pojedino tijelo trenje djeluje u suprotnom smjeru od brzine kojom kliže uz drugo tijelo, i zove se trenje klizanja. Trenje klizanja pretvara kinetičku energiju u toplinu. Statičko trenje sprečava klizanje, i jednakog je iznosa a suprotnog smjera od zbroja ostalih sila koje pokušavaju izazvati klizanje. Ako se te sile povećavaju, te njihov zbroj premaši maksimalni mogući iznos statičkog trenja (graničnu vrijednost), počinje klizanje a statičko trenje se pretvara u trenje klizanja. Granična vrijednost statičkog trenja najčešće se ne razlikuje značajno od iznosa trenja klizanja, ali ponekad može biti i znatno veća (na primjer metal na metalu ili staklo na staklu), a iznimno i malo manja. Iznos sile trenja ne ovisi neposredno o veličini dodirne površine, nego samo o kemijskom sastavu i obradi ploha. Trenje je posljedica kemijskog međudjelovanja (električne sile) materijala koji su u dodiru.[2]
Vrste trenja
Trenje mirovanja
Trenje mirovanja otpor je početku gibanja tijela. Iskustvo pokazuje da je sila potrebna za održavanje gibanja manja od sile potrebne za pokretanje tijela i da je trenje najveće neposredno prije početka gibanja. Zbog toga je na primjer zaustavni put automobila kraći ako kotači nisu do kraja blokirani (ABS sustav kočenja).
Trenje klizanja
Trenje klizanja razmjerno je komponenti sile kojom tijelo djeluje okomito na podlogu, to jest sili kojom jedna površina pritišće drugu. Sila koja podržava klizanje nekoga tijela jednolikom brzinom iznosom je jednaka sili trenja, ali suprotnoga je smjera. Ako na tijelo koje se giba ne djeluje sila u smjeru njegova gibanja, tijelo će se zbog trenja nakon nekog vremena zaustaviti. Što je trenje veće, zaustavljanje je brže. Trenjem kinetička energija tijela prelazi u toplinu. Taj se učinak može i iskoristiti, na primjer glavica šibice trenjem se može zagrijati na temperaturu potrebnu da se smjesa zapali.
Iznos trenja klizanja
Iznos trenja klizanja između dva tijela proporcionalan je sili kojom se tijela međusobno stišću na plohi dodira. U najjednostavnijem slučaju ravne dodirne plohe, iznos trenja klizanja [math]\displaystyle{ \scriptstyle T }[/math] računa se tako da se ukupni iznos sile [math]\displaystyle{ \scriptstyle N }[/math] kojom jedno tijelo pritišće drugo pomnoži brojem koji se zove koeficijent trenja klizanja [math]\displaystyle{ \scriptstyle \mu }[/math]:
- [math]\displaystyle{ T= \mu N \,. }[/math]
Koeficijent trenja klizanja ovisi o vrsti i obradi dodirnih ploha; na primjer za automobilsku gumu na suhom asfaltu iznosi oko 0,80 - 0,85 (ako guma nije izlizana), a za istu gumu na mokrom asfaltu oko 0,45 - 0,50, dok je na zaleđenom kolniku samo 0,05 - 0,10.[3] Iznos sile kojom jedno tijelo pritišće drugo uobičajeno se obilježava slovom [math]\displaystyle{ \scriptstyle N }[/math], zato što ta sila djeluje okomito, tj. u smjeru normale, na dodirnu plohu i smjer klizanja.
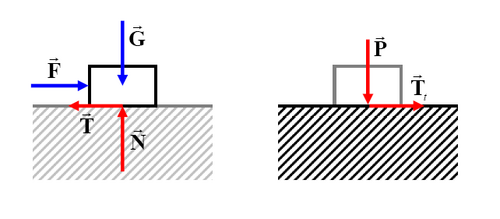
Na skici desno prikazan je jednostavan primjer trenja za tijelo koje kliže po vodoravnoj podlozi zato što ga gura vodoravna sila [math]\displaystyle{ \scriptstyle \vec F }[/math] (podloga je drugo tijelo, koje smatramo velikim i nepomičnim, odnosno čije gibanje nas ne zanima). Na lijevoj strani skice ucrtane su sile koje djeluju na tijelo, a na desnoj sile kojima tijelo djeluje na podlogu.
Na tijelo djeluje težina [math]\displaystyle{ \scriptstyle \vec G }[/math] kojom ga privlači Zemlja; zbog težine tijelo pritišće na podlogu (koja mu ne dopušta gibanje u tome smjeru) jednakom silom [math]\displaystyle{ \scriptstyle \vec P }[/math] (desna strana skice). Na silu [math]\displaystyle{ \scriptstyle \vec P }[/math] podloga uzvraća (zakon akcije i reakcije) normalnom reakcijom [math]\displaystyle{ \scriptstyle \vec N }[/math] koja u suprotnom smjeru djeluje na tijelo. Tako se vertikalne sile na tijelo ([math]\displaystyle{ \scriptstyle \vec G }[/math] i [math]\displaystyle{ \scriptstyle \vec N }[/math]) poništavaju.
Sila [math]\displaystyle{ \scriptstyle \vec F }[/math] pokreće i ubrzava klizanje tijela po podlozi. Zbog toga se tijelo tare o podlogu, tj. djeluje na nju silom trenja koja je na desnoj strani skice označena kao [math]\displaystyle{ \scriptstyle \vec {T}_{t} }[/math]. Na tu silu podloga uzvraća (zakon akcije i reakcije) silom trenja [math]\displaystyle{ \scriptstyle \vec T }[/math] koja u suprotnom smjeru djeluje na tijelo. Ukratko, djelovanju sile [math]\displaystyle{ \scriptstyle \vec F }[/math] na tijelo suprotstavlja se sila trenja klizanja [math]\displaystyle{ \scriptstyle \vec T }[/math], čiji se iznos računa prema gore navedenoj formuli, i umanjuje ubrzanje tijela.
U rutinskom rješavanju problema s trenjem nije doista potrebno provoditi opisanu uzročno-posljedičnu analizu sila. U navedenom primjeru, dovoljno je samo prikazati sve sile koje djeluju na tijelo (lijeva strana skice) i odrediti ubrzanje tijela pomoću Newtonovog temeljnog zakona gibanja: vektorski zbroj sila jednak je umnošku mase i ubrzanja. Ubrzanje je u smjeru sile [math]\displaystyle{ \scriptstyle \vec F }[/math], a protivi mu se [math]\displaystyle{ \scriptstyle \vec T }[/math], pa je: [math]\displaystyle{ \scriptstyle F - T = ma }[/math]. U vertikalnom smjeru nema ubrzanja, što znači da vektorski zboj vertikalnih sila iznosi nula, tj. [math]\displaystyle{ \scriptstyle N = G }[/math], čime se dobiva iznos normalne reakcije pomoću kojega se računa trenje [math]\displaystyle{ \scriptstyle T = \mu N }[/math]. Uvrštavajući za iznos težine [math]\displaystyle{ \scriptstyle G = mg }[/math] konačno se dobiva jednadžba za akceleraciju [math]\displaystyle{ \scriptstyle F - \mu mg = ma }[/math]. Ako je sila koja gura tijelo 20 N, masa tijela 2 kg, a koeficijent trenja 0,8, uvrštavanje daje 20 - 0,8 · 2 · 9,81 = 2a, pa je ubrzanje a = 2,15 m/s2.
I u slučaju da sustav sila nije tako jednostavan (npr. tijelo je na kosini a vuče ga ili gura više sila pod proizvoljnim kutevima), problem se riješava na sličan način. Tada u pravilu normalna reakcija podloge (potrebna za određivanje trenja) neće biti jednaka težini tijela, ali se na sličan način dobiva iz temeljnog zakona gibanja, uz rastavljanje sila u prikladno odabranom koordinatnom sustavu. U gornjem jednostavnom primjeru, umjesto formalnog uvođenja koordinatnog sustava, korišteno je razdvajanje sila na vodoravne i okomite.
Statičko trenje (ponekad se kaže i trenje mirovanja) sprečava klizanje koje pokušavaju uzrokovati druge sile. Primjerice, ako čovjek malom silom gura neki težak ormar, ormar se ne miče. To znači da pod djeluje na ormar točno jednakom silom statičkog trenja u suprotnom smjeru. Kako čovjek mijenja iznos sile kojom gura, tako se mijenja i iznos statičkog trenja (sve dok ormar miruje): statičko trenje je upravo onoliko koliko je potrebno da spriječi klizanje. No, statičko trenje ne može premašiti granični iznos [math]\displaystyle{ \scriptstyle T_M = \mu_S N }[/math] koji se računa na isti način kao i trenje klizanja, ali pomoću koeficijenta statičkog trenja [math]\displaystyle{ \scriptstyle \mu_S }[/math] koji je u pravilu veći od koeficijenta trenja klizanja [math]\displaystyle{ \scriptstyle \mu }[/math]. Stoga se statičko trenje u načelu opisuje relacijom:
- [math]\displaystyle{ T \leq \mu_\mathrm{S} N }[/math]
Za mnoge materijale [math]\displaystyle{ \scriptstyle \mu_S }[/math] je tek za nekoliko postotaka veći od [math]\displaystyle{ \scriptstyle \mu }[/math]. No za neke kombinacije metalnih ploha mogu se razlikovati i nekoliko puta, na primjer za cink na lijevanom željezu statički koeficijent je 0,85 dok je koeficijent trenja klizanja samo 0,21.
Za cjeloviti opis statičkog trenja i trenja klizanja najjednostavnije je promatrati lijevu stranu gornje skice, te zamisliti da se iznos sile [math]\displaystyle{ \scriptstyle F }[/math] koja gura tijelo povećava od nule do vrijednosti znatno veće od graničnog iznosa statičkog trenja. Na skici desno prikazano je kako se pri tome mijenja iznos sile trenja [math]\displaystyle{ \scriptstyle T }[/math] koja se protivi sili [math]\displaystyle{ \scriptstyle F }[/math]. Dok tijelo miruje, statičko trenje raste jednako kao i sila [math]\displaystyle{ \scriptstyle F }[/math], sve do iznosa [math]\displaystyle{ \scriptstyle T_M = \mu_S N }[/math]. Nakon toga, povećanje sile [math]\displaystyle{ \scriptstyle F }[/math] uzrokuje klizanje, a iznos statičkog trenja pada na iznos trenja klizanja.
Na skici se još opaža i da iznos trenja klizanja nije posve konstantan (kako se podrazumijevalo u prethodnom opisu). Oscilacije u iznosu trenja klizanja (na skici su preuveličane radi bolje uočljivosti) ne ovise neposredno o sili [math]\displaystyle{ \scriptstyle F }[/math], nego su posljedica mikroskopskih neravnina dodirnih ploha koje prilikom gibanja utječu na kemijske interakcije među materijalima (crtež je proizvoljan, tj. samo kvalitativno ilustrira tipične mjerene vrijednosti).[4]
Zaključci
Iz prethodnog razlaganja možemo stvoriti ove zaključke:
- trenje klizanja ovisi o težini tijela odnosno o okomitom pritisku na podlogu;
- trenje klizanja ovisi o vrsti i hrapavosti materijala;
- trenje klizanja je manje od težine tijela;
- trenje mirovanja je veće od trenja klizanja (gibanja);
- kod manje brzine gibanja trenje klizanja je veće.
Trenje kotrljanja
Trenje kotrljanja nastaje pri kotrljanju cilindričnog ili sfernog tijela. Razmjerno je opiranju tijela i podloge elastičnim i plastičnim deformacijama koje se pojavljuju pri takvu gibanju. Manje je od trenja klizanja. Faktor trenja kotrljanja na primjer čelika na čeliku iznosi 0,002 do 0,004, to jest oko sto puta je manji nego koeficijent trenja klizanja za isti materijal.
Otpor fluida
Otpor fluida gibanju čvrstog tijela ovisi o gustoći i viskoznosti fluida, o obliku tijela i njegovu položaju u struji fluida, hrapavosti njegove površine, a razmjeran je ploštini tijela okomitoj na smjer gibanja. Otpor plinova pri malim relativnim brzinama razmjeran je brzini, a pri velikim brzinama kvadratu brzine, otpor tekućina razmjeran je kvadratu i višim potencijama brzine. Otpor fluida najčešće se izračunava prema jednadžbi: R = CwPρv²/2, gdje je Cw faktor otpora, koji ovisi o glatkoći površina i o obliku, dimenzijama i položaju tijela u struji fluida (manji faktor otpora imaju tijela aerodinamičnog oblika), P ploština tijela okomita na smjer gibanja, ρ gustoća fluida, v brzina gibanja tijela. Primjerice, ubrzanje tijela koje slobodno pada kroz fluid pod utjecajem sile teže se s povećanjem brzine smanjuje i pri nekoj brzini, kada se otpor fluida izjednači sa silom teže, postaje jednaka nuli te se tijelo dalje giba jednoliko. Tako na primjer prije otvaranja padobrana padobranac može postići brzinu do 270 km/h (zračni otpor).
Stokesov zakon
Stokesov zakon, u hidrodinamici, glasi: sferno tijelo koje se giba u viskoznoj tekućini svladava silu otpora Fd koja iznosi:
- [math]\displaystyle{ F_d = 6 \cdot \pi \cdot \mu \cdot r \cdot v }[/math]
gdje je: η - dinamička viskoznost, v - brzina tijela, r - polumjer.
Stokesov zakon, u optici, glasi: valna duljina luminiscentnoga zračenja uvijek je veća ili jednaka valnoj duljini istovrsnoga zračenja koje ju je izazvalo. [5]
Trenje u atmosferi
Trenje u atmosferi djelovanje je tangencijalne sile između slojeva koji se kreću različitim brzinama; nastaje zbog turbulentnoga gibanja zraka i ovisi o utjecaju neravne podloge tla na strujanje zraka. Trenje koje nastaje gibanjem molekula zraka, to jest molekula dušika i kisika (viskoznost zraka), može se, u usporedbi s turbulentnim trenjem, potpuno zanemariti. Zbog trenja vjetar ne puše usporedno s izobarama, nego ih siječe; pritom na Sjevernoj polutki ostaje niski tlak zraka lijevo i sprijeda s obzirom na puhanje vjetra (Buys-Ballotov ili barički zakon vjetra). Strujeći u visinu, vjetar skreće zbog trenja na Sjevernoj polutki u desno, jačina mu postupno raste pa tek na visini od 1 kilometar postaje geostrofički vjetar. Vektor vjetra mijenja se u prizemnom sloju po takozvanoj Ekmanovoj spirali.
Značaj trenja
Trenje ima vrlo veliko značenje kod različitih strojeva. Ono može biti štetno i korisno. Trenje je štetno kod onih strojeva čiju snagu želimo iskoristiti za pogon bilo kojeg radnog stroja, na primjer dizalice, alatnog stroja, vozila i tako dalje, jer se jedan dio snage stroja mora utrošiti na svladavanje trenja različitih strojnih dijelova. Međutim, trenje može biti i korisno, jer bez trenja ne bismo imali kočnice kod vozila ni kod različitih drugih strojeva. Kotači kod kojih se gibanje prenosi od jednog na drugi pomoću trenja zovu se frikcioni kotači ili tarenice. Takvi se kotači koriste na primjer kod frikcione preše ili preše na trenje.[6]
Korisni učinci trenja u svakodnevnom životu
Ljudi šeću naprijed odguravajući se nogama natrag. Bez trenja, podovi, ceste i pločnici bili bi mnogo više kliski nego ledeno klizalište. Automobili ne bi mogli ubrzavati ni kočiti. Ljudi bi padali na pod kada bi pokušali hodati ili trčati.
Paljenje vatre
Najjednostavnija oprema za paljenje vatre ovisi o trenju, a sastoji se od dvaju suhih drvenih štapova. Rukama ili strunom luka treba brzo rotirati jedan štap po drugom. Trenje postiže temperaturu do približno 300°C, pri kojoj štap počne žariti. Za paljenje šibica također se primjenjuje trenje. Kada se glava šibice tare o traku na bočnoj strani kutije od šibica, trenje podiže temperaturu. Vrućina potakne da kemikalije u glavi šibice i u traci na kutiji od šibica zajedno reagiraju. Kako se temperatura povećava, glava šibice izgara na zraku i naposljetku zapali drvo.
Problemi koje uzrokuje trenje
Trenje predstavlja značajan problem kod predmeta koje treba gibati po podlozi. Rani ljudi su povlačili terete na drvenim saonicama. Te su saonice pomogle u prijenosu tereta, ali je još uvijek ostalo veliko trenje između saonica i tla. Ljudi su poslije otkrili da je teške terete kao npr. blokove od kamena mnogo lakše pomicati pomoću valjaka. Valjci su se okretali, te su smanjili trenje jer teret nije klizao dodirajući tlo kao kad se gibao. Nedostatak je valjka što oni ostaju iza tereta kada se teret kreće po njima. Pred otprilike 5500 godina taj je problem bio prevladan izumom kombinacije kotača i osovine.
Iskoristivost trenja u industriji
Zavarivanje trenjem
Zavarivanje trenjem je vrsta zavarivanja pritiskom, gdje se dijelovi između dodirnih površina zagrijavaju toplinom trenja nastalom vrtnjom jednog ili obaju dijelova koji se zavaruju, nakon čega slijedi zavarivanje povećanim pritiskom na dijelove, uz istovremenu obustavu vrtnje. Zavari su rotacijski simetrični. Postoji više načina zavarivanja trenjem. Mogu se zavarivati metali i njihove legure, ali i tvrdi polimeri. Moguće je međusobno zavarivanje raznovrsnih metalnih materijala.
Valjni i kuglični ležaji
Kako je trenje kotrljanja manje od trenja klizanja, kod različitih osovina upotrebljavamo kuglične ili valjkaste ležaje čime trenje klizanja pretvaramo u trenje kotrljanja.
Tarna spojka
Podrobniji članak o temi: Tarna spojkaTarna spojka je spojka koja služi za povremeno uključivanje u rad radnog (gonjenog) stroja pri neprekidnom radu pogonskog stroja. Kod ukapčanja (pokretanja) dolazi do klizanja pri čemu se gubi snaga, koja se pretvara u toplinu, a pokazuje se kao veće ili manje trošenje ploha. U normalnom pogonu brzine se moraju izjednačiti i spojke rade bez klizanja. Vrlo slične po konstrukciji (a često identične) su tarne kočnice. [7]
Tarne spojke mogu biti: [8]
- Kandžasta tarna spojka
- Pločasta tarna spojka
- Radijalna tarna spojka
- Tarne spojke s jednom lamelom
- Tarne spojke s više lamela
Izvori
- ↑ trenje, [1] "Hrvatska enciklopedija", Leksikografski zavod Miroslav Krleža, www.enciklopedija.hr, 2015.
- ↑ Kulišić P., Mehanika i toplina, Školska knjiga, Zagreb, 1996
- ↑ Kako voziti sigurno, sup.hr
- ↑ Young H. D., Freedman R. A., Sears and Zemansky University Physics, Addison-Wesley, San Francisco (2004)
- ↑ Stokes, George Gabriel, [2] "Hrvatska enciklopedija", Leksikografski zavod Miroslav Krleža, www.enciklopedija.hr, 2015.
- ↑ Velimir Kruz: "Tehnička fizika za tehničke škole", "Školska knjiga" Zagreb, 1969.
- ↑ [3] "Elementi strojeva", Fakultet elektrotehnike, strojarstva i brodogradnje Split, Prof. dr. sc. Damir Jelaska, 2011.
- ↑ "Spojke", prof. dr. sc. Boris Obsieger, Tehnički fakultet Rijeka, 2004.