Reuleauxov trokut

Reuleauxov poligon je krivulja konstantne širine – to jest, krivulja čiji su svi promjeri iste duljine. Najpoznatiji oblik je Reuleauxov trokut. Ime je dobio po Franzu Reuleauxu, njemačkom inženjeru iz 19. stoljeća, mada je takav trokut bio poznat i prije njega.
Reuleauxov trokut najjednostavniji je netrivijalni primjer krivulje s konstantnom širinom – krivulja kod koje su jednako udaljene dvije suprotne paralelne tangente, nebitno od smjera tih paralela. (Trivijalni primjer je krug.)
Konstrukcija
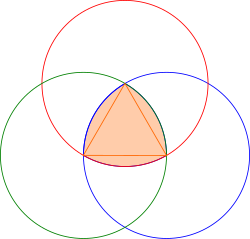
Konstrukcija Reuleauxovog trokuta počinje na jednakostraničnom trokutu. Šestar se postavi u jedan od vrhova i opiše kružni luk između druga dva vrha. To se ponovi i za ostale vrhove. Zatim se obriše početni trokut. Rezultat je krivulja konstantne širine. Ekvivalentno, za zadani trokut T čije su stranice a, uzeti granicu presjeka kružnica s polumjerom a koje su konstruirane iz vrhova trokuta T.
Po Blaschke-Lebesgue teoremu, Reuleauxov trokut ima najmanju površinu od svih krivulja konstantne širine. Ta površina je , gdje je d konstantni promjer, što je za oko 11,4 % manje od površine kruga istog promjera.[1]
Reuleauxov trokut može se generalizirati na pravilne poligone s neparnim brojem stranica. Tako su, na primjer, izrađene britanske kovanice od 20[2] i 50[3] penija.[4]
Primjena

- Rotor Wankelova motora sličan je Reuleauxovom trokutu.
- Svrdlom u obliku Reuleauxovog trokuta može se izbušiti rupa koja je skoro savršen kvadrat (98,77 % površine, sa zaobljenim kutovima). Takvo svrdlo je 1914. projektirao i patentirao Harry Watts.[1] To je svrdlo konkavno na tri mjesta, što omogućuje sječenje kutova kvadrata i odstranjivanje strugotine. Vođenje osi svrdla je po kružnici, kao što pokazuje slika desno.
Trodimenzionalna inačica
Presjek lopti polumjera r iz središta pravilnog tetraedra čija je stranica r zove se Reuleauxov tetraedar, ali nije ploha konstantne širine. No, može se napraviti da bude ploha s konstantnom širinom, koji se zove Meissnerov tetraedar, tako što se bridni lukovi zamijene krivim umetcima; alternativno, rotacijska ploha Reuleauxovog trokuta kroz jednu njegovu os simetrije formira plohu konstantne širine, s najmanjim obujmom od svih rotacijskih ploha zadane konstantne širine.
Izvori
- ↑ 1,0 1,1 Miodrag Petković, Zanimljivi svet matematike, str. 196-197, Tehnička knjiga, Beograd 1994. ISBN 86-325-0401-0
- ↑ Kovanica od 20 penija je Reuleauxov sedmerokut
- ↑ Kovanica od 50 penija je Reuleauxov sedmerokut
- ↑ Anić - Goldstein, Rječnik stranih riječi, Zagreb 2007, ISBN 978-953-6045-52-5, str. 200, odrednica "Funta", "...manje jedinice nazivaju se u V. Britaniji peni".
Vanjske poveznice
- Drilling Square Holes - Bušenje kvadratnih rupa
- Weisstein, Eric W. "Reuleaux Triangle." From MathWorld--A Wolfram Web Resource. - Reuleauxov trokut na Web stranici MathWorld
