Tangenta: razlika između inačica
Bot: Automatski unos stranica |
m Zamjena teksta - '<!--'''T(.*)'''-->' u '' |
||
| Redak 1: | Redak 1: | ||
[[Image:Graph_of_sliding_derivative_line.gif|thumb|350px|Tangenta na krivulju]] | |||
'''Tangenta''' ili '''dodirnica''' je [[pravac]] koji dodiruje [[krivulja|krivulju]] u jednoj [[Točka (geometrija)|točki]]. Na svaku je krivulju (npr. [[kružnica|kružnicu]], [[elipsa|elipsu]], [[parabola (krivulja)|parabolu]], [[hiperbola (krivulja)|hiperbolu]]) moguće položiti beskonačno mnogo tangenata, ali kroz svaku točku glatke krivulje prolazi samo jedna tangenta. | '''Tangenta''' ili '''dodirnica''' je [[pravac]] koji dodiruje [[krivulja|krivulju]] u jednoj [[Točka (geometrija)|točki]]. Na svaku je krivulju (npr. [[kružnica|kružnicu]], [[elipsa|elipsu]], [[parabola (krivulja)|parabolu]], [[hiperbola (krivulja)|hiperbolu]]) moguće položiti beskonačno mnogo tangenata, ali kroz svaku točku glatke krivulje prolazi samo jedna tangenta. | ||
Posljednja izmjena od 22. lipanj 2025. u 06:06
Tangenta ili dodirnica je pravac koji dodiruje krivulju u jednoj točki. Na svaku je krivulju (npr. kružnicu, elipsu, parabolu, hiperbolu) moguće položiti beskonačno mnogo tangenata, ali kroz svaku točku glatke krivulje prolazi samo jedna tangenta.
Jednadžba pravca tangente je y - y0 = k(x - x0), pri čemu je koeficijent smjera k jednak derivaciji funkcije krivulje u točki x0 tj. k = f'(x0), pod uvjetom da navedena derivacija postoji.
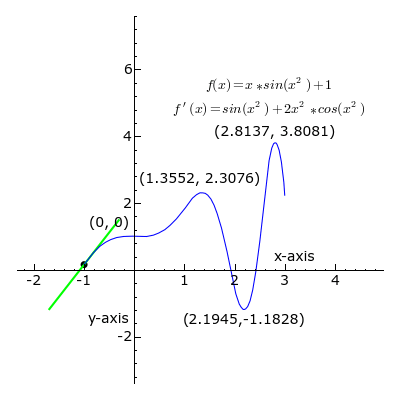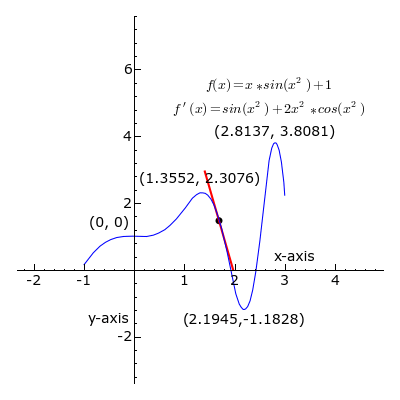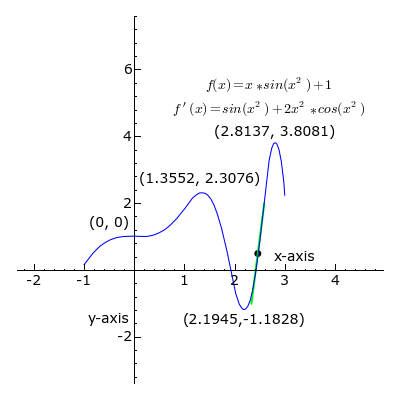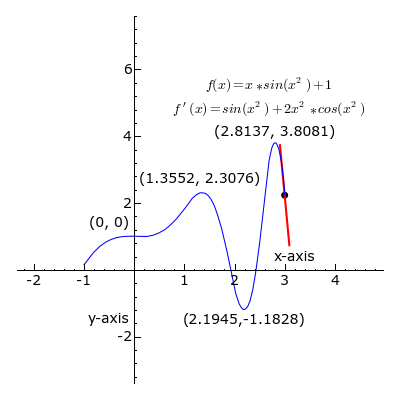
Na slici desno prikazana je krivulja složene funkcije:
- f(x) = xsin(x2) + 1
u dvodimenzionalnom koordinatnom sustavu (x,y).
U svakoj točki krivulje (u intervalu od x = -1 do x = 3) prikazana je tangenta na krivulju.
Kada je koeficijent smjera tangente (odnosno prva derivacija funkcije) pozitivan, k > 0, dio pravca tangente je zelene boje.
Kada je koeficijent smjera tangente negativan, k < 0, dio pravca tangente je crvene boje.
Kada je koeficijent smjera tangente jednak nuli, k = 0, tj. kad funkcija ima lokalni ekstrem (minimum ili maksimum), dio pravca tangente je crne boje.