Prosti broj

Prirodni brojevi od 0 do 100. Prosti brojevi su označeni crvenom bojom.

Eratostenovo sito do broja 120

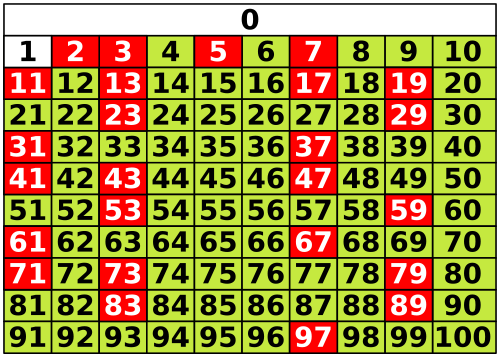
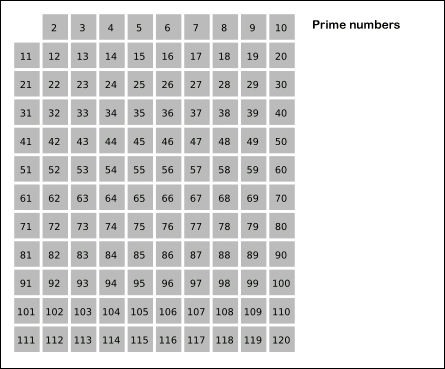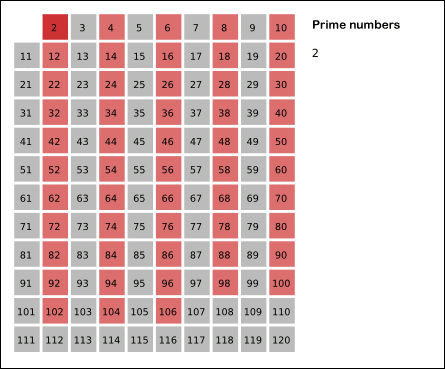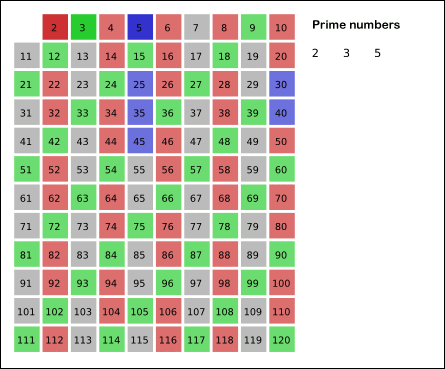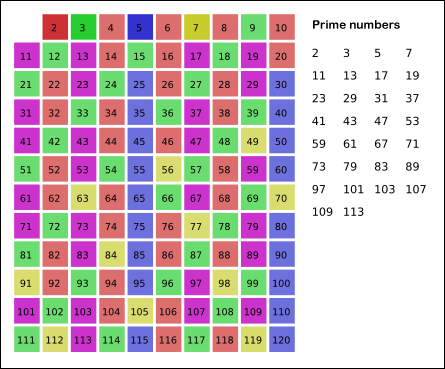
Prosti brojevi ili primbrojevi su svi prirodni brojevi veći od 1 koji su bez ostatka djeljivi samo s brojem 1 i sami sa sobom. Prirodni brojevi veći od 1 koji nisu prosti brojevi nazivaju se složenim brojevima. Na primjer, broj 5 je prost jer je djeljiv samo s 1 i 5, dok je 6 složen jer se osim s 1 i 6 može podijeliti i brojevima 2 i 3.

Osnovni teoremi vezani uz strukturu prostih brojeva

Euklidov teorem

Ovdje ćemo metodom kontradikcije dokazati Euklidov teorem koji kaže da prostih brojeva ima beskonačno mnogo. Pretpostavimo da je [math]\displaystyle{ P }[/math] konačan skup svih prostih brojeva,

[math]\displaystyle{ P = \{p_1, p_2,\dots, p_n\} }[/math]

i promotrimo broj

[math]\displaystyle{ N = p_1 \cdot p_2 \cdot ... \cdot p_n + 1. }[/math]

Očito je ostatak pri dijeljenju ovog broja svakim od prostih brojeva iz [math]\displaystyle{ P }[/math] jednak jedan,

[math]\displaystyle{ N \equiv 1 \pmod {p_i}, \forall i = \{1, 2, ..., n\} }[/math]

pa [math]\displaystyle{ N }[/math] nije djeljiv ni sa jednim od njih. No prema Osnovnom stavku aritmetike svaki bi se broj morao moći zapisati kao umnožak konačno mnogo prostih brojeva, a za ovakav [math]\displaystyle{ N }[/math] to ne može biti nijedan broj iz skupa [math]\displaystyle{ P }[/math]. Očito postoje prosti brojevi izvan tog skupa, čime se početna tvrdnja dovodi u kontradikciju.

Prostih brojeva oblika [math]\displaystyle{ 4n + 3 }[/math] ima beskonačno mnogo

Dokažimo sada da prostih brojeva oblika [math]\displaystyle{ 4n + 3 }[/math] ima beskonačno mnogo. Prije svega, jasno je da neparni prosti brojevi mogu isključivo biti u obliku [math]\displaystyle{ 4n + 1 }[/math] ili [math]\displaystyle{ 4n + 3. }[/math] Uočimo da vrijedi [math]\displaystyle{ (4s + 1)(4t + 1) = 4(4st + s + t) + 1, }[/math] tj. umnožak dva prosta broja oblika [math]\displaystyle{ 4n + 1 }[/math] je i sam tog oblika.

Pretpostavimo da je [math]\displaystyle{ S =\{ p_1, p_2, ..., p_n\} }[/math] skup svih prostih brojeva oblika [math]\displaystyle{ 4n + 3. }[/math]

Konstruirajmo sada neparni broj [math]\displaystyle{ m = 4p_1p_2 \cdot ... \cdot p_n - 1. }[/math] Očito [math]\displaystyle{ m }[/math] daje ostatak 3 pri dijeljenju s 4 pa barem jedan njegov prosti faktor nije u obliku [math]\displaystyle{ 4n + 1, }[/math] odnosno barem je jedan faktor u obliku [math]\displaystyle{ 4n + 3. }[/math] Jasno je da niti jedan od [math]\displaystyle{ p_1, p_2, ..., p_n }[/math] ne dijeli [math]\displaystyle{ m }[/math] jer očito [math]\displaystyle{ m }[/math] daje ostatak [math]\displaystyle{ - 1, }[/math] tj. [math]\displaystyle{ p_i - 1, }[/math] pri dijeljenju s [math]\displaystyle{ p_i, i =\{1, 2, ..., n\}. }[/math] To znači da postoji još barem jedan prosti broj oblika [math]\displaystyle{ 4n + 3 }[/math] izvan [math]\displaystyle{ S, }[/math] kontradikcija.

Razmak između prostih brojeva

Važno svojstvo prostih brojeva je da ne postoji najveći razmak između dva prosta broja. To je zbog toga što postoji proizvoljno velik skup uzastopnih složenih brojeva između svaka dva prosta broja. Takav skup je primjerice

[math]\displaystyle{ S = \{n! + 2, n! + 3, ..., n! + n : n \in \mathbb{N}\},n \gt 1. }[/math]

Ovo vrijedi jer je svaki broj [math]\displaystyle{ n! + 2, ..., n! + n }[/math] redom djeljiv s 2, 3, ..., n pa su brojevi složeni.

Ipak, jasno je da ovo ne dokazuje da postoji beskonačno mnogo parova prostih brojeva [math]\displaystyle{ p_1, p_2 }[/math] koji su udaljeni za točno [math]\displaystyle{ k. }[/math] Tome svjedoči tzv. hipoteza o prostim brojevima blizancima koja kaže da postoji beskonačno mnogo prostih brojeva koji su udaljeni za točno 2, no ta hipoteza do danas nije dokazana. Isto tako, nije dokazano da postoji beskonačno mnogo parova prostih brojeva čija je je razlika jednaka [math]\displaystyle{ k }[/math]. Primijetimo da je ova tvrdnja izravna posljedica toga da hipoteza o prostim brojevima blizancima nije dokazana.

Uz to, nije dokazano ni da za svaki [math]\displaystyle{ k \in \mathbb{N} }[/math] možemo naći neka dva prosta broja [math]\displaystyle{ p_1 \lt p_2 }[/math] takva da je [math]\displaystyle{ p_2 - p_1 = k }[/math].

Uloga prostih brojeva

Prosti brojevi služe pri faktorizaciji, odnosno rastavljanju složenih brojeva na proste ili prim-faktore.

Svaki se složeni broj može na jedinstven način rastaviti na nekoliko prim-faktora, a ako je broj [math]\displaystyle{ p }[/math] prost tada je jedina takva faktorizacija očito [math]\displaystyle{ p = p \cdot 1 }[/math].

  125|5      34|2
   25|5      17|17
    5|5       1 
    1
  
  125=5*5*5   34=2*17

Neka pravila djeljvosti

Ako je broj paran (zadnja znamenka mu je 2, 4, 6, 8 ili 0) onda je djeljiv s prostim brojem 2.

Ako broj završava znamenkama 5 ili 0 onda je djeljiv s prostim brojem 5.

Ako mu je zbroj znamenaka djeljiv s 3, onda je taj broj djeljiv s 3.

Ako mu je dvoznamenkasti završetak djeljiv s brojem 4, onda je taj broj djeljiv s 4.

Ova pravila možemo međusobno kombinirati. Na primjer, ako je broj djeljiv i s 2 i s 3, onda je taj broj zacijelo djeljiv i s brojem 6.

Ako je troznamenkasti broj djeljiv s 8, onda je taj broj djeljiv s 8,

Ako je zbroj znamenaka nekog broja djeljiv s 9, onda je taj broj djeljiv s 9.

Vrijede dakako i obrati svih navedenih tvrdnji.

Zanimljivosti

Poznata je rečenica velikog švicarskog matematičara Leonharda Eulera vezana uz proste brojeve:

Matematičari su uzalud do danas pokušavali otkriti pravilnost u slijedu prostih brojeva, a mi imamo razloga vjerovati da je to misterija u koju ljudski um nikada neće prodrijeti.

Vanjske poveznice

• Primbrojevi na mrežnom izdanju Hrvatske enciklopedije

Nedovršeni članak Prosti broj koji govori o matematici treba dopuniti. Dopunite ga prema pravilima uređivanja Hrvatske internetske enciklopedije.