Jedinična kružnica
Jedinična, brojevna ili trigonometrijska kružnica definirana je kao kružnica sa središtem u ishodištu koordinatnog sustava (0, 0) i polumjerom odnosno radijusom 1. Jedinična kružnica siječe x-os u točkama (-1,0) i (1,0) i y-os u točkama (0, 1) i (0, -1).
Ortogonalna projekcija točke [math]\displaystyle{ A(x,y) }[/math] na x-os je [math]\displaystyle{ A_1(x,0) }[/math], a na y-os [math]\displaystyle{ A_2(0,y) }[/math]. Dužine [math]\displaystyle{ OA_1 }[/math] i [math]\displaystyle{ OA_2 }[/math] su katete pravokutnog trokuta [math]\displaystyle{ OA_1A_2 }[/math] čije su dužine x i y.
[math]\displaystyle{ \cos\theta }[/math] je horizontalna, a [math]\displaystyle{ \sin\theta }[/math] vertikalna dužina. Kut [math]\displaystyle{ \theta }[/math] je u standardnom položaju. Prema definicijama funkcija sinus i kosinus dobivamo sljedeće jednakosti:
- [math]\displaystyle{ \sin \theta = \frac{y}{1} =y }[/math]
- [math]\displaystyle{ \cos \theta=\frac{x}{1}=x }[/math]
- [math]\displaystyle{ \operatorname{tg} \theta=\frac{y}{x} }[/math]
Ako su (x, y) točke na kružnici u prvom kvadrantu, onda su x i y katete pravokutnog trokuta (isječci na x i y osi, respektivno) čija je hipotenuza (polumjer) 1. Prema Pitagorinom poučku x i y zadovoljavaju jednadžbu
- [math]\displaystyle{ x^2 + y^2 = 1 }[/math]
Budući da uvijek vrijedi [math]\displaystyle{ x^2 = (-x)^2 }[/math], prethodna jednadžba vrijedi za sve točke (x, y) na jediničnoj kružnici, a ne samo za prvi kvadrant.
Trigonometrijske funkcije
Uz pomoć trigonometrijskih funkcija kod pravokutnih trokuta mogu se prikazati odnosi između koordinata i kutova na jediničnoj kružnici. Trigonometrijske funkcije sinus i kosinus mogu se na jediničnoj kružnici definirati na sljedeći način: ako je (x, y) točka na jediničnoj kružnici i ako dužina od ishodišta do točke (x, y) čini kut t s pozitivnim dijelom apscise (u smjeru suprotnim od smjera kazaljke na satu), tada vrijedi:
- [math]\displaystyle{ \cos\theta = x }[/math]
- [math]\displaystyle{ \sin\theta = y }[/math]
Jednadžba [math]\displaystyle{ x^2 + y^2 = 1 }[/math] daje poznatu relaciju
- [math]\displaystyle{ \cos^ 2\theta + \sin^ 2\theta = 1 }[/math]
| α | sin α | cos α | tg α | cotg α | |
|---|---|---|---|---|---|
| 1. kvadrant | 0–90° | + | + | + | + |
| 2. kvadrant | 90–180° | + | − | − | − |
| 3. kvadrant | 180–270° | − | − | + | + |
| 4. kvadrant | 270–360° | − | + | − | − |
Jedinična kružnica također daje uvid da su sinus i kosinus periodične funkcije jednakostima:
- [math]\displaystyle{ \cos t = \cos \left(2k\pi +t\right) }[/math]
- [math]\displaystyle{ \sin t = \sin \left(2k \pi +t \right) }[/math]
za svaki cijeli broj k.
Ove jednakosti polaze od činjenice da x i y koordinate točke na krugu ostaju iste ako kut t napravi bilo koji broj okreta po kružnici (1 okret = 360° = 2π radijana).
Pri radu s pravokutnim trokutima, sinus i kosinus, kao i ostale trigonometrijske funkcije imaju smisla samo ako je kut veći od 0 i manji od [math]\displaystyle{ \frac{\pi}{2} }[/math]. Koristeći jediničnu kružnicu, ove funkcije dobivaju smisao za bilo koju realnu vrijednost kuta. Ako je točka A točka jedinične kružnice onda su njene koordinate
- [math]\displaystyle{ A(0)=A(2 \pi)=(1,0) }[/math]
- [math]\displaystyle{ A(\pi/2)= (0,1) }[/math]
- [math]\displaystyle{ A(\pi)=(-1,0) }[/math]
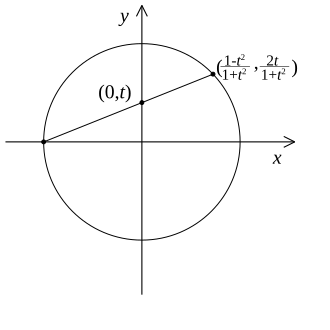
Druge točke su određene koordinatama [math]\displaystyle{ \left(\frac{1-t^2}{1+t^2},\frac{2t}{1+t^2}\right) }[/math]
Zamjenom [math]\displaystyle{ t=\frac{p}{q} }[/math] dobivamo Pitagorine trojke [math]\displaystyle{ (q^2-p^2, 2pq, q^2+p^2) }[/math].
Kompleksna ravnina
U kompleksnoj ravnini jedinična kružnica predstavljena je skupom [math]\displaystyle{ G \subset \mathbb{C} }[/math]
- [math]\displaystyle{ G = \{z : \operatorname{Re}(z)^2 + \operatorname{Im}(z)^2 = 1 \} = \{z : z = e^{i\phi}, 0 \leq \phi \lt 2\pi\} }[/math]
Jedinična kružnica pojavljuje se i u polarnom rastavu kompleksnog broja:
- [math]\displaystyle{ z = r e^{i\varphi} = r \left(\cos \varphi + i \sin \varphi\right) = r \operatorname{cis} \phi }[/math]
Faktor eiφ koji opisuje fazu broja nalazi se na jediničnoj kružnici.
Ta kružnica ima i druga korisna svojstva. Primjerice, bilo koja realna potencija broja na jediničnoj kružnici također se nalazi na jediničnoj kružnici, što olaškava potenciranje kompleksnih brojeva:
- [math]\displaystyle{ z^a = r^a \left(e^{i\varphi}\right) ^a = r^a e^{i a \varphi} = r^a \operatorname{cis} a\varphi }[/math]