Dopplerov efekt

Dopplerov učinak je promjena frekvencije valova pri relativnom gibanju njihova izvora ili promatrača.

U prometu se s pomoću Dopplerova učinka i radara može odrediti brzina kretanja vozila.

Dopplerov učinak se može primijetiti i kod kretanja labuda po vodi (valovi na vodi).

Crveni pomak (gore) i plavi pomak (dolje).

Spektralne linije udaljene galaksije u usporedbi sa Sunčevim (lijevo).

Dopplerov učinak ili Dopplerov efekt je promjena frekvencije valova pri relativnom gibanju njihova izvora ili promatrača. Opaža se kod svakoga valnoga gibanja kao povećanje, odnosno smanjenje frekvencije kada se izvor valova i promatrač međusobno približavaju, odnosno udaljavaju. Umjesto frekvencije izvora f₀, opaža se frekvencija f:

[math]\displaystyle{ f = \left( \frac{c + v_\text{r}}{c - v_\text{s}} \right) \cdot f_0 \, }[/math]

gdje je:

[math]\displaystyle{ c \; }[/math] - brzina valova u sredstvu (na primjer u zraku);

[math]\displaystyle{ v_\text{r} \, }[/math] - relativna brzina promatrača; pozitivna ako se promatrač približava prema izvoru (negativna za udaljavanje);

[math]\displaystyle{ v_\text{s} \, }[/math] - relativna brzina izvora; pozitivna ako se izvor približava prema promatraču (negativna za udaljavanje).

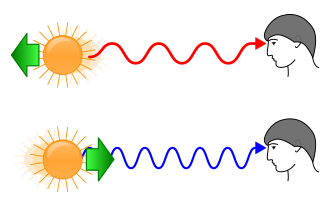
Kod zvučnih valova Dopplerov učinak opaža se kao povišenje ili sniženje tona: na primjer ton raznih vozila čini se viši za vrijeme približavanja a niži prilikom udaljavanja. Kod svjetlosnih valova spektralne linije pomaknute su prema ljubičastomu dijelu spektra ako se izvor približava (plavi pomak), a prema crvenome (crveni pomak) ako se udaljava. Prema teoriji relativnosti u tom slučaju vrijedi:

[math]\displaystyle{ f = f_0 \cdot \sqrt{1-v^2/c^2\,} \cdot (1+\frac{v \cdot \cos\alpha}{c}) }[/math]

gdje je: c - brzina svjetlosti, a α - kut izvora prema promatraču: α = 90° kod transverzalnoga gibanja, pa se to naziva transverzalni (poprečni) Dopplerov učinak. U astronomiji se primjenom Dopplerova učinka mjeri brzina radijalnoga gibanja nebeskih tijela (na primjer male promjene brzine zvijezda pod utjecajem planeta, brzine gibanja galaktika) ili njihovih dijelova (brzina rotacije, brzina pulsiranja). U prometu se s pomoću Dopplerova učinka i radara može odrediti brzina kretanja vozila; u medicini, brzina protoka krvi (ehosonografija).

Objašnjenje

Dopplerov učinak otkrio je Christian Doppler 1842. na osnovu proučavanja promjene frekvencije svjetlosti koju emitiraju zvijezde u dvojnom sustavu (dvije zvijezde koje se okreću jedna oko druge), ali Dopplerov učinak pokusima je potvrdio C. H. D. Buys Ballot 1845. na utrechtskoj željezničkoj postaji uspoređujući zvuk trubača koji stoje na jednom mjestu i trubača koji se gibaju.

Ta se promjena može opaziti u barem dvije različite pojave. Prvi je primjer razlika u visini tona kod automobila (ili vlaka) koji se približava te onog koji se udaljava. To se opažanje temelji na različitim gustoćama zvučnih valova tijela koji se približava od onog koji se udaljava. Ako nam se automobil približava, fronte postaju gušće, te frekvencija zvuka kojeg čujemo raste. U obrnutom slučaju, fronte su rjeđe i frekvencija pada.

Drugi primjer je u opažanju svjetlosti svjetlećeg objekta koji se nekom brzinom približava ili se udaljava od promatrača. Bitno je spomenuti da se crveni pomak, prvenstveno razlikuje od plave po načinu da valovi poprimaju fotonsku frekvenciju zvuka.

Matematičko objašnjenje

Ako se izvor zvuka giba brzinom v_r, bit će za promatrača prividna duljina zvučnog vala λ₁ kraća ako se približava, a ako se udaljava bit će prividna duljina zvučnog vala λ₂ dulja od normalne valne duljine λ kada izvor zvuka miruje. Ako je c brzina zvuka, onda je kod približavanja put valova manji, te iznosi:

[math]\displaystyle{ (c - v_r) \cdot t = f \cdot \lambda_1 \cdot t }[/math]

Kako je:

[math]\displaystyle{ \lambda_1 = \frac{c}{f_1} }[/math]

pri čemu je f₁ prividna frekvencija zvuka za promatrača kada izvor zvuka se približava, pa ispada:

[math]\displaystyle{ (c - v_r) \cdot t = f \cdot \frac{c}{f_1} \cdot t }[/math]

Podijelimo li jednadžbu s c∙t, dobit ćemo:

[math]\displaystyle{ 1 - \frac{v_r}{c} = \frac{f}{f_1} }[/math]

pa je prividna frekvencija izvora zvuka koji se približava:

[math]\displaystyle{ f_1 = \frac{f}{1 - \frac{v_r}{c}} }[/math]

Kada se izvor zvuka udaljava:

[math]\displaystyle{ (c + v_r) \cdot t = f \cdot \lambda_2 \cdot t }[/math]

Kako je:

[math]\displaystyle{ \lambda_2 = \frac{c}{f_2} }[/math]

pri čemu je f₂ prividna frekvencija zvuka za promatrača kada izvor zvuka se udaljava, pa ispada:

[math]\displaystyle{ (c + v_r) \cdot t = f \cdot \frac{c}{f_2} \cdot t }[/math]

Odatle na isti način kao i prije izlazi da je prividna frekvencija izvora zvuka koji se udaljava:

[math]\displaystyle{ f_2 = \frac{f}{1 + \frac{v_r}{c}} }[/math]

Crveni pomak

Podrobniji članak o temi: Crveni pomak

Crveni pomak je pomak spektralnih linija svjetlosti (povećanje valnih duljina) prema crvenom dijelu spektra. Općenitije, pomak spektralnih linija elektromagnetskih valova prema većim valnim duljinama u spektru. Nastaje kad se izvor elektromagnetskih valova udaljava, što je brže udaljavanje izvor veći je crveni pomak (Dopplerov učinak) ili kad se izvor elektromagnetskih valova nalazi u snažnom gravitacijskom polju, a emitirani se valovi šire prema slabijem gravitacijskom polju. Kozmički crveni pomak odražava opće širenje svemira (Hubbleov zakon). Gravitacijski crveni pomak nastaje gubitkom energije fotona u gravitacijskome polju. Dokazan je Mössbauerovim učinkom i zapažen je u spektrima zvijezda s jakim gravitacijskim poljem.

Vanjske poveznice

• Crveni pomak
• Plavi pomak