Comptonov učinak

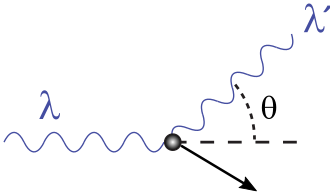
Comptonov učinak: foton valne duljine $\lambda$ koji dolazi s lijeve strane, sudara se sa slobodnim elektronom, pa se zatim stvara novi foton valne duljine $\lambda '$ koji se raspršuje pod kutem $\theta$.

U pojednostavljenom Bohrovom modelu atoma vodika, Balmerova serija nastaje skokom elektrona na drugu energetsku razinu (n = 2). Prikazana je emisija kvanta svjetlosti. Prijelaz elektrona prestavlja H-alfa, prvu liniju Balmerove serije, valne duljine 656 nm.

Energije fotona na 500 keV i elektrona nakon Comptonovog raspršenja.

Skica Comptonovog pokusa: Comptonovo raspršenje događa se u grafitu s lijeve strane. Katodne zrake (elektroni) prolaze rendgenske fotone raspršene pod određenim kutom. Energija raspršenog fotona mjeri se Braggovim raspršenjem u kristalu s desne strane u kombinaciji s ionizacijskom komorom; komora je mogla mjeriti ukupnu energiju taloženu tijekom vremena, a ne energiju pojedinih raspršenih fotona.

Comptonov učinak u atomu.

Comptonov učinak ili Comptonov efekt (prema A. H. Comptonu) je porast valne duljine elektromagnetskog zračenja raspršenoga na slobodnim elektronima. Vrijedi izraz:

$\lambda '-\lambda ={\frac {h}{m_{e}\cdot c}}\cdot (1-\cos {\theta })$

gdje je:

$\lambda$ - početna valna duljina elektromagnetskog zračenja,

$\lambda '$ - valna duljina elektromagnetskog zračenja nakon raspršenja,

$h$ - Planckova konstanta,

$m_{e}$ - masa elektrona (9,10938215(45)×10⁻³¹ kg),

$c$ - brzina svjetlosti, i

$\theta$ - kut između upadnog i raspršenoga zračenja.

Izvorno je taj porast valne duljine otkriven pri raspršenju rendgenskoga zračenja na atomima kemijskih elemenata male atomske mase, kod kojih je energija vezanja elektrona zanemariva u odnosu na energiju kvanta zračenja.

Objašnjenje

Prema čestičnoj ili korpuskularnoj teoriji moramo česticama monokromatske svjetlosti pripisati određenu energiju i impuls sile. Po Einsteinu se svjetlost frekvencije ν sastoji od kvanata energije E:

$E=h\cdot \nu$

Da bi pronašli impuls sile treba poći od osnovnih odnosa teorije relativnosti. Svjetlost ima konstantnu brzinu. Da bismo pak uveli impuls kvanta svjetlosti, možemo se osloniti na osnovni odnos između energije i mase:

$E=m\cdot c^{2}$

Prema tome masa kvanta svjetlost iznosi:

$m={\frac {h\cdot \nu }{c^{2}}}$

Kako je impuls sile umnožak mase m i brzine svjetlosti c, dobivamo za impuls kvanta svjetlost izraz:

$p={\frac {h\cdot \nu }{c}}={\frac {h}{\lambda }}$

Energija i impuls kvanata svjetlosti dolazi najjasnije do izražaja u Comptonovom učinku. A. H. Compton je 1922. puštao na lake kemijske elemente rendgenske zrake i analizirao raspršene zrake. Rendgenske zrake koje prolaze kroz materiju u pravolinijskom smjeru ništa ne mijenjaju. Naprotiv, raspršene zrake pod nekim kutom pokazuju promjene u valnoj duljini. Valne duljine se povećavaju. Taj učinak objasnili su istovremeno Compton i P. Debye hipotezom o kvantima svjetlosti. Pri prolazu kroz materiju kvanti svjetlosti srazuju se s elektronima i gube nešto na energiji i impulsu sile, a time se umanjuje frekvencija. Compton i Debye su obradili srazove između kvanata svjetlosti i elektrona na osnovu mehaničkih zakona o očuvanju energije i impulsa, i uspjeh je bio golem.

Energije kvanata rendgenskih zraka mnogo su veće od onih energija kojima su elektroni vezani uz atom. Pri srazovima možemo elektrone smatrati slobodnim česticama. Osim toga njihove su brzine razmjerno male, pa nećemo učiniti velike pogreške ako uzmemo da prije sraza miruju. Kad kvant svjetlosti naleti na takav mirni elektron, on se odbija od njega nakoso, prenoseći dio svojeg impulsa i energije na elektron. Impuls sile kvanta svjetlosti prije sraza jednak je h∙ν/c, poslije sraza h∙(ν - Δν)/c. Zadobiveni impuls elektrona jednak je m’∙v, gdje je m’ masa u gibanju.

Impuls kvanta svjetlosti prije sraza mora biti jednak zbroju impulsa elektrona i kvanta svjetlosti poslije sraza:

$m'^{2}\cdot v^{2}={\frac {h^{2}\cdot \nu ^{2}}{c^{2}}}+{\frac {h^{2}\cdot (\nu -\Delta \nu )^{2}}{c^{2}}}-2\cdot {\frac {h\cdot \nu }{c}}\cdot {\frac {h\cdot (\nu -\Delta \nu )}{c}}\cdot \cos \theta$

Desnu stranu jednadžbe možemo dalje pisati (za omjer ν/c uvodimo oznaku β):

${\frac {m^{2}\cdot v^{2}}{1-\beta ^{2}}}=2\cdot {\frac {h^{2}\cdot \nu ^{2}}{c^{2}}}-2\cdot {\frac {h^{2}\cdot \nu \cdot \Delta \nu }{c^{2}}}+{\frac {h^{2}\cdot \Delta \nu ^{2}}{c^{2}}}-2\cdot {\frac {h^{2}\cdot \nu ^{2}}{c^{2}}}\cdot \cos \theta +2\cdot {\frac {h^{2}\cdot \nu \cdot \Delta \nu }{c^{2}}}\cdot \cos \theta$

Ovu jednadžbu podijelit ćemo sa m²c², pa članove dalje srediti:

${\frac {\beta ^{2}}{1-\beta ^{2}}}=({\frac {h\cdot \nu }{m\cdot c^{2}}})^{2}\cdot [2\cdot (1-\cos \theta )-2\cdot {\frac {\Delta \nu }{\nu }}\cdot (1-\cos \theta )]+({\frac {h\cdot \Delta \nu }{m\cdot c^{2}}})^{2}$

Prema osnovnim trigonometrijskim jednadžbama je:

$\cos \theta =\cos ^{2}{\frac {\theta }{2}}-\sin ^{2}{\frac {\theta }{2}}=1-2\cdot \sin ^{2}{\frac {\theta }{2}}$

pa našu jednadžbu možemo pisati u obliku:

${\frac {\beta ^{2}}{1-\beta ^{2}}}=4\cdot ({\frac {h\cdot \nu }{m\cdot c^{2}}})^{2}\cdot [(1-{\frac {\Delta \nu }{\nu }})\cdot \sin ^{2}{\frac {\theta }{2}}]+({\frac {h\cdot \Delta \nu }{m\cdot c^{2}}})^{2}$

Ova jednadžba slijedi iz načela o održanju impulsa. Sada treba da još uzmemo u račun i zakon o očuvanju energije. Srazom kvanta svjetlosti dobiva elektron kinetičku energiju m’∙c² - m∙c², a ta energija mora biti jednaka gubitku energije svjetlosti:

$m'\cdot c^{2}-m\cdot c^{2}=h\cdot \nu -h\cdot (\nu -\Delta \nu )$

Dijeleći ovu jednadžbu sa m∙c² i prenoseći prvi član s lijeve na desnu stranu, dobivamo:

${\frac {1}{\sqrt {1-\beta ^{2}}}}=1+{\frac {h\cdot \Delta \nu }{m\cdot c^{2}}}$

${\frac {1}{1-\beta ^{2}}}=1+2\cdot {\frac {h\cdot \Delta \nu }{m\cdot c^{2}}}+({\frac {h\cdot \Delta \nu }{m\cdot c^{2}}})^{2}$

${\frac {\beta ^{2}}{1-\beta ^{2}}}=2\cdot {\frac {h\cdot \Delta \nu }{m\cdot c^{2}}}+({\frac {h\cdot \Delta \nu }{m\cdot c^{2}}})^{2}$

Ovaj izraz treba sada uvrstiti u jednadžbu impulsa:

$2\cdot {\frac {h\cdot \Delta \nu }{m\cdot c^{2}}}+({\frac {h\cdot \Delta \nu }{m\cdot c^{2}}})^{2}=4\cdot ({\frac {h\cdot \nu }{m\cdot c^{2}}})^{2}\cdot (1-{\frac {\Delta \nu }{\nu }})\cdot \sin ^{2}{\frac {\theta }{2}}+({\frac {h\cdot \Delta \nu }{m\cdot c^{2}}})^{2}$

Kako odatle vidimo, kvadratni se članovi u Δν poništavaju, što znači veliko pojednostavljenje. Dakle dobivamo:

$\Delta \nu =2\cdot {\frac {h\cdot \nu ^{2}}{m\cdot c^{2}}}\cdot (1-{\frac {\Delta \nu }{\nu }})\cdot \sin ^{2}{\frac {\theta }{2}}$

To možemo dalje pisati u obliku:

$c\cdot {\frac {\Delta \nu }{\nu \cdot (\nu -\Delta \nu )}}=2\cdot {\frac {h}{m\cdot c}}\cdot \sin ^{2}{\frac {\theta }{2}}$

No izraz s lijeve strane nije ništa drugo nego promjena valne duljine:

$\Delta \lambda =\lambda '-\lambda ={\frac {c}{\nu -\Delta \nu }}-{\frac {c}{\nu }}={\frac {c\cdot \Delta \nu }{(\nu -\Delta \nu )\cdot \nu }}$

Promjena valne duljine svjetlosti, zbog sraza s elektronima, jednaka je:

$\Delta \lambda =2\cdot {\frac {h}{m\cdot c}}\cdot \sin ^{2}{\frac {\theta }{2}}$

To je rezultat Comptona i Debyea. Promjena valne duljine svjetlosti je veća ako je zraka jače otklonjena na stranu. Svojstvena konstanta ima dimenziju duljine i zove se Comptonova valna duljina:

${\frac {h}{m\cdot c}}=0,024\cdot 10^{-10}\,{\mbox{m}}$

Najvažnije je u Comptonovoj jednadžbi da je povećanje valne duljine jednaka za sve valne duljine.

Mjerenja na raspršenim rendgenskim zrakama potpuno su potvrdila teoretsku jednadžbu o povećanju valne duljine s kutom otklona. No još više, motrenja elektrona u Wilsonovoj komori, koji bivaju ubrzani udarcima kvanata svjetlosti, potpuno potvrđuju teorijska shvaćanja. W. Bothe i H. Geiger pokusima su pokazali da je raspršenje rendgenskih zraka i izbijanje elektrona iz njihovih atoma istodobni proces. Time je sraz između kvanata svjetlosti i elektrona osvijetljen sa svih strana.

Hipotezom o kvantima svjetlosti stvoren je nepomirljiv sukob u klasičnoj fizici. Korpuskularna slika svjetlosti, doduše, ispravno tumači niz važnih promatranja, ali ta ista korpuskularna teorija potpuno zatajuje kod poznatih pojava, kao što su interferencija i ogib (difrakcija ). Pojave kod kojih se međusobno poništava svjetlost ili kod kojih svjetlost zakreće "oko ugla" dadu se rastumačiti samo valnom teorijom. Širenje svjetlosti u prostoru može se prikazati samo valnom teorijom. Treba se sjetiti samo velikog područja geometrijske optike, pa se odmah vidi nužnost valne teorije svjetlosti. Pojava svjetlosti kao vala u svim tim mnogobrojnim pokusima potpuno je dokazana.

Međutim, prema fotoelektričnom učinku i Comptonovom učinku isto je tako siguran i opstanak kvanta svjetlosti. U okviru klasične fizike to dualističko pojavljivanje svjetlosti zamrsuje se u nerješivu suprotnost. Kao fizička pojava može svjetlost u klasičnoj teoriji biti val ili čestica. Prihvaćanje jedne pretpostavke isključuje drugu. Pokusi pokazuju međutim suprotno. Dualističko pojavljivanje svjetlosti osnovna je crta kvantne zakonitosti koja prožima prirodu.