Ubrzanje


Ubrzanje ili akceleracija (oznaka a) je vektorska fizikalna veličina koja opisuje promjenu brzine s vremenom, a određena je derivacijom brzine v po vremenu t:
Ubrzanje opisuje promjenu iznosa brzine (povećavanje ili smanjivanje) ili smjera brzine ili oboje. Za smanjivanje brzine koriste se još izrazi deceleracija i retardacija. Ako je ubrzanje stalno, gibanje se naziva jednoliko ubrzanim, jednoliko usporenim, odnosno jednolikim kružnim gibanjem. Mjerna jedinica ubrzanja jest metar u sekundi na kvadrat (m/s2). Ako se vektoru brzine mijenja samo smjer, kao na primjer u jednolikom kružnom gibanju, to se ubrzanje naziva kutno ubrzanje ili kutna akceleracija. [1]
Najjednostavnije je opisivati ubrzanje i brzinu gibanja materijalne točke. Takav se opis odnosi i na tijela kojima su dimenzije zanemarivo male (čestice) i na kruta tijela koja ne rotiraju, to jest gibaju se samo pravocrtno (translacijski). Ako tijelo još i rotira, njegove različite točke imaju različita ubrzanja. Tada se pojam ubrzanje tijela odnosi na ubrzanje njegovog centra masa (a kaže se još da je to translacijsko ili linearno ubrzanje), a usto se još promatra i kutno ubrzanje.
Formalna definicija
Ubrzanje je derivacija brzine po vremenu:[2]
- .
Simbol označava ubrzanje (a je prvo slovo riječi akceleracija koja je latinskog porijekla), simbol označava brzinu; i jedna i druga veličina su funkcije vremena t (što se podrazumijeva, pa se ne mora eksplicitno navesti). Ubrzanje opisuje kako se brzo i u kojemu smjeru mijenja brzina u pojedinom trenutku. Budući da je brzina vektorska veličina koja može mijenjati i iznos i smjer, ubrzanje istovremeno opisuje i jednu i drugu promjenu. No, one se mogu razdvojiti tako da se zasebno promatraju tangencijalno i normalno ubrzanje.
Analiza gibanja u dinamici često polazi od 2. Newtonovog aksioma, koji (u nerelativističkoj aproksimaciji) glasi: Suma sila jednaka je umnošku mase i akceleracije (to jest ). Odatle se, iz sila koje djeluju na materijalnu česticu, izravno dobiva njezina akceleracija. Potom se iz akceleracije brzina čestice računa integriranjem:
gdje je brzina u trenutku (takozvana početna brzina). (A potom se iz brzine može odrediti jednadžba putanje ili pređeni put. Ako se umjesto materijalne točke promatra tijelo, navedena razmatranja odnose se na gibanje njegovog centra masa.)
Prosječno i trenutno ubrzanje
Za gore navedenu definiciju ponekad se kaže da opisuje trenutno ili pravo ubrzanje. Ti se pojmovi koriste (umjesto jednostavnog naziva ubrzanje) kada se želi naglasiti razlika u odnosu na prosječno ili srednje ubrzanje , koje se definira kao omjer promjene brzine i vremenskog intervala u kojemu se brzina promijenila:
gdje simbol označava promjenu, to jest razliku između kasnije i ranije vrijednosti. Tu je promjena brzine od trenutka do trenutka , dok je vremeski interval (proteklo vrijeme) između ta dva trenutka.
Tijekom promatranog vremenskog intervala točka (ili tijelo) je mogla kojekako ubrzavati i usporavati svoje gibanje, pa će se istim postupkom dobiti različita prosječna ubrzanja u kraćim vremenskim podintervalima, što ograničava upotrebnu vrijednost prosječnog ubrzanja na zadani vremenski interval (i njegov zadani početni trenutak).
Nasuprot tome, "pravo" ubrzanje ("trenutno") ne ovisi o vremenskom intervalu jer se dobiva njegovim zamišljenim skraćivanjem na "beskonačno mali interval" oko pojedinog trenutka. Postupak se općenito (u različitim primjenama) naziva graničnim prijelazom i definira pojam derivacije. Trenutno ubrzanje je derivacija brzine po vremenu, to jest "granična vrijednost" (limes, simbol "lim") omjera promjene brzine i pripadnog vremenskog intervala kada vremenski interval "teži" prema nuli:
- .
Definicija "promjena brzine u jedinici vremena"
Najjednostavnija definicija ubrzanja, koja je dobro polazište za razumijevanje pojma, jest uobičajena definicija iz osnovne škole: Ubrzanje je promjena brzine u jedinici vremena. Pritom se obično promatra pravocrtno gibanje, pa se riječ brzina odnosi samo na iznos brzine (jer ne mijenja smjer) a i riječ ubrzanje samo na iznos ubrzanja. Takva definicija vrlo nepotpuno opisuje ubrzanje: to je samo broj koji je jednak prosječnom iznosu ubrzanja u toj jedinici vremena.
No ako promatramo jednoliko ubrzano pravocrtno gibanje, kod kojega se iznos ubrzanja ne mijenja, onda je on doista jednak prosječnom iznosu, i računa se tako da se promjena brzine podjeli s vremenom. Na primjer ako za 3 sekunde brzina naraste s 5 m/s na 17 m/s, ukupna promjena je 12 m/s, a ubrzanje se dobiva dijeljenjem (12 m/s) : (3 s) = 4 m/s2, i označava da brzina naraste za 4 m/s svake sekunde. Odatle se vidi i da je metar u sekundi na kvadrat (m/s2) mjerna jedinica za ubrzanje u SI sustavu.
Tangencijalno i normalno ubrzanje
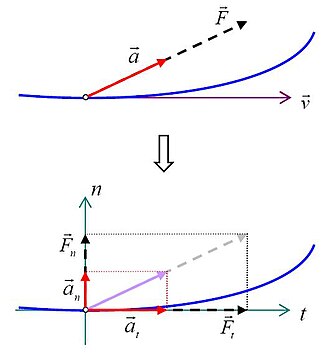
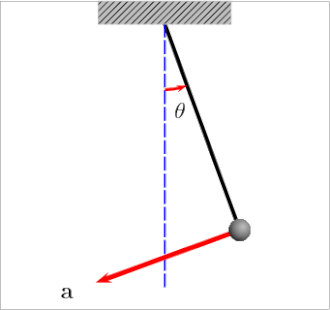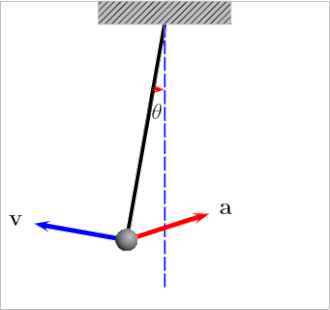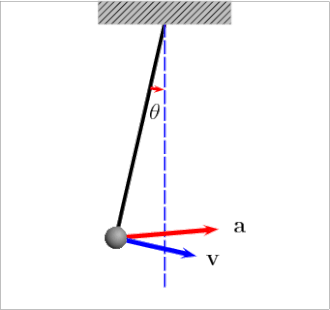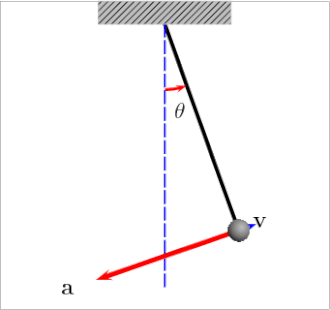
U svakoj točki proizvoljno zakrivljene putanje neke materijalne čestice može se njezino ubrzanje rastaviti na dvije komponente: na tangencijalno ubrzanje koje je paralelno s tangentom na putanju, i na normalno ubrzanje koje je u smjeru normale na putanju. Na skici desno prikazano je u gornjem dijelu ukupno ubrzanje (i sila koja ga uzrokuje), a u donjem dijelu to ubrzanje rastavljeno je na tangencijalnu i normalnu komponentu (kao i sila). Prikazane su i tangenta i normala (t i n) kao koordinatne osi: tangenta je u smjeru brzine , a normala je okomita na tangentu, leži u ravnini koju određuju brzina i ukupno ubrzanje, i usmjerena je prema "udubljenom" dijelu putanje. (Uobičajeno korištenje istog slova t i za tangentu i za vrijeme ne bi smjelo dovesti do zabune: ono se u tekstu odnosi na tangentu samo ako je indeks tangencijalnog vektora ili komponente.)
Tangencijalno ubrzanje opisuje kako se brzo mijenja iznos brzine:
- .
Tu je skalarna tangencijalna komponenta ubrzanja, dok je iznos brzine.
Normalno ubrzanje opisuje kako se brzo mijenja smjer brzine:
- .
Tu je skalarna normalna komponenta ubrzanja, je iznos brzine, dok je radijus zakrivljenosti putanje u promatranoj točki.
Na skici su prikazane vektorske komponente, a u gornjem tekstu se koriste skalarne komponente. Odnos između njih i ukupnog ubrzanja je sljedeći:
- .
Tu je jedinični vektor u smjeru tangente (dakle, i u smjeru brzine), dok je jedinični vektor u smjeru normale (jedinični vektori imaju iznos jednak 1). Kada se skalarna komponenta pomnoži s jediničnim vektorom, dobije se vektorska komponenta, npr. .
Za razumijevanje uloge komponenti ubrzanja korisno je razmotriti njihovu vezu sa silama na temelju 2. Newtonovog zakona. Ako je ukupna (rezultantna) sila koja djeluje na česticu, ona joj daje ubrzanje u smjeru sile prema formuli . Temeljno svojstvo vektora jest da među njihovim komponentama na pojedinoj osi koordinatnog sustava vrijede isti odnosi (jednadžbe) kao i među samim vektorima. To znači da tangencijalna sila daje tangencijalno ubrzanje, a normalna sila daje normalno ubrzanje (kao na skici).
Odatle se lako razumije zašto tangencijalno i normalno ubrzanje imaju gore navedeni smisao. Tangencijalna sila djeluje u smjeru brzine (ili u suprotnom smjeru); dakle, ona povećava iznos brzine (ili ga umanjuje). Zato tangencijalno ubrzanje opisuje promjenu iznosa brzine (povećanje ili umanjenje). Dakle, nema razloga da se te tangencijalne komponente dovode u vezu s promjenom smjera brzine.
Nasuprot tome, normalna sila okomita je na brzinu: ona ne povećava brzinu jer ne vuče nimalo prema naprijed, niti umanjuje brzinu jer ne vuče nimalo prema natrag. A ipak mijenja brzinu jer daje čestici ubrzanje (normalno ubrzanje). Budući da nema promjene iznosa brzine, očito je da to mora biti promjena smjera brzine.
Formalni izvod
Formule za tangencijalno i normalno ubrzanje mogu se dokazati deriviranjem brzine ako se ona prikaže kao umnožak iznosa i jediničnog vektora:
- .
Jedinični vektor tangente ima smjer brzine, i može se dobiti tako da se brzina podijeli sa svojim iznosom (zato što je njegov iznos jednak 1). Deriviranjem gornjeg izraza za brzinu, prema pravilu deriviranja umnoška, dobije se:
- .
Odmah se vidi da lijevi pribrojnik izgleda kao ranije definirana tangencijalna komponenta ubrzanja. No, da bi se to dokazalo, treba pokazati da je desni pribrojnik jednak normalnoj komponenti ubrzanja. U tu svrhu treba objasniti što se dobiva deriviranjem jediničnog vektora u desnom pribrojniku.
Derivacija jediničnog vektora
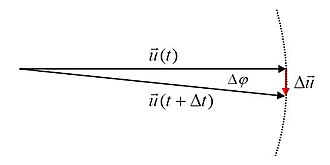
Derivacija bilo kojeg jediničnog vektora mora biti okomita na njega, kako se vidi iz skice desno, koja prikazuje promjenu nekog jediničnog vektora u vremenskom intervalu . Na skici je ta promjena približno okomita na jedinični vektor, a u graničnom prijelazu kada vremenski interval teži nuli (kad se računa derivacija), promjena postaje točno okomita na jedinični vektor (i to u smjeru njegova zakretanja). Iznos derivacije dobije se tako da se iznos promjene podijeli s i provede granični prijelaz u kojemju vremenski interval teži nuli. Na skici se vidi da je iznos promjene približno jednak duljini kružnoga luka kojega prekriva, a u graničnom prijelazu postaju točno jednaki. Duljina tog dijela kružnoga luka jednaka je kutu zakreta kako slijedi iz definicije kuta u radijanima (luk kroz polumjer), jer je iznos polumjera jednak 1 (iznos jediničnog vektora). Dakle, iznos derivacije jediničnog vektora je granična vrijednost , a to je iznos kutne brzine zakretanja jediničnog vektora .
Odatle se vidi da desni pribrojnik gornje jednadžbe za ubrzanje ima smjer jediničnog vektora normale te da ima iznos . To je, dakle, doista normalna komponenta ubrzanja, i ona ima oblik:
- .
Analogija s kružnim gibanjem
Kod kružnog gibanja iznos kutne brzine jednak je omjeru iznosa brzine i polumjera kružnice, . Tu kutna brzina opisuje zakretanje polumjera (radij-vektora) povučenog do točke koja se giba po kružnici. No, ista kutna brzina opisuje i zakretanje vektora brzine točke, jer je taj vektor stalno okomit na polumjer kružnice. Zato se normalna komponenta ubrzanja može izraziti preko iznosa brzine i polumjera: .
Po analogiji s kružnim gibanjem, i kod gibanja po krivulji opisuje se zakretanje vektora brzine pomoću iznosa brzine, i to relacijom . Ta relacija zapravo definira polumjer zakrivljenosti krivulje u promatranoj točki. Polumjer zakrivljenosti krivulje je polumjer tzv. oskulatorne kružnice, a to je kružnica koja najbolje prianja uz krivulju u toj točki (imaju jednaku zakrivljenost). Definiranje polumjera zakrivljenosti omogućuje da se normalna komponenta ubrzanja na krivulji izrazi na sličan način kao na kružnici:
- .
Alternativni geometrijski izvod
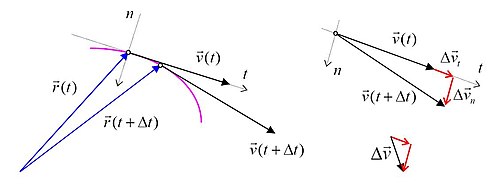
Prethodni izvod orijentiran je na matematičku korektnost i potpunost, pa mu zato nedostaje neposrednog geometrijskog zora. Na skici desno, međutim, zorno je prikazano gibanje točke po krivulji tako da se vide vektori položaja i brzine na početku i na kraju vremenskog intervala (lijeva strana skice), kao i promjena brzine na desnoj strani skice. Pritom je promjena brzine rastavljena na tangencijalnu i normalnu komponentu:
- .
Ubrzanje je derivacija brzine po vremenu, tj. granična vrijednost omjera promjene brzine i pripadnog vremenskog intervala kada vremenski interval teži nuli:
- .
I bez punog matematičkog formalizma, može se razumjeti kako lijevi pribrojnik daje tangencijalnu komponentu a desni normalnu komponentu ubrzanja. Iz skice je očito da samo mijenja iznos brzine (u prikazanom primjeru povećava brzinu). Smjer brzine mijenja samo komponenta , ali ona malo doprinosi i promjeni iznosa, jer prevodi katetu pravokutnog trokuta u hipotenuzu . Međutim, kada u graničnom prijelazu teži prema nuli (kod izračuna ubrzanja), taj pravokutni trokut postaje jednakokračan, pa mijenja samo smjer vektora brzine.[3]
Odatle je jasno da je skalarna tangencijalna komponenta ubrzanja jednaka derivaciji iznosa brzine po vremenu - te da je pozitivna kad se brzina povećava, a negativna kad se brzina umanjuje. Skalarna normalna komponenta ubrzanja uvijek je pozitivna, jer se brzina zakreće u smjeru normale. Njezin iznos, međutim, određuje se na temelju gornjeg formalnog izvoda, ili na temelju analize kružnog gibanja. (Ipak, i sa skice se razabire da taj iznos treba biti jednak , zato što je iznos približno jednak umnošku iznosa brzine i kuta njezinoga zakretanja.)
Jednostavni slučajevi: ubrzanje na pravcu i na kružnici
Ubrzano gibanje po pravcu i jednoliko gibanje po kružnici zanimljivi su primjeri zato što sadrže samo jednu od opisanih komponenata ubrzanja. Kod gibanja po pravcu, to je samo tangencijalno ubrzanje (jer brzina ne mijenja smjer). Kod jednolikog gibanja po kružnici, to je samo normalno ubrzanje (jer brzina ne mijenja iznos), a ono se na kružnici naziva centripetalnim ili radijalnim ubrzanjem.
Jednoliko i jednoliko ubrzano gibanje po pravcu najjednostavniji su primjeri gibanja, na kojima učenici osnovnih i srednjih škola tek upoznaju veličine pomoću kojih se gibanje opisuje - znatno prije nego što će učiti npr. o vektorima ili o derivacijama. Na toj razini znanja, i brzina i ubrzanje se opisuju kao skalarne veličine. Kaže se da je ubrzanje promjena brzine u jedinici vremena, te da je pozitivno kada brzina raste a negativno kad se brzina umanjuje. Za jednoliko ubrzano gibanje po pravcu, takve su definicije "operativno korektne" jer omogućuju točan izračun brzine i pređenoga puta (barem za gibanje tijela na istu stranu; manje komplikacije nastaju ako se počne vraćati). U konceptualno korektnom opisu, ubrzanje je vektor koji ne može biti niti pozitivan niti negativan; a skalar koji se koristi u formulama je skalarna tangencijalna komponenta ubrzanja.
Kod jednolikog gibanja po kružnici uvodi se pojam centripetalnog ubrzanja koji i bez punog vektorskog formalizma jasno ocrtava smisao normalne komponente ubrzanja. A kod jednoliko ubrzanog gibanja po kružnici mora se - pored centripetalnog ubrzanja - uvesti i tangencijalno ubrzanje za opis promjene iznosa brzine. Time je zapravo obuhvaćen glavni smisao rastava ubrzanja na normalnu i tangencijalnu komponentu, čak i ako se ne koristi formalni vektorski opis.
Izvori
- ↑ ubrzanje (akceleracija), [1] "Hrvatska enciklopedija", Leksikografski zavod Miroslav Krleža, www.enciklopedija.hr, 2016.
- ↑ Young H. D., Freedman R. A., Sears and Zemansky University Physics, Addison-Wesley, San Francisco (2004)
- ↑ I. Levanat: Fizika za TVZ - Kinematika i dinamika Tehničko veleučilište u Zagrebu (2010)




















































