Kartografska projekcija

Kartografska projekcija je postupak kojim se zakrivljena ploha, kao što je Zemljina površina ili površine drugih nebeskih tijela, preslikava u ravninu.[1] Korištenje kartografske projekcije neizbježno je pri izradi karata, pa otuda i naziv.
Proučavanje kartografskih projekcija daje matematičku osnovu za izradu preciznih zemljovida. Osim kartografije, kartografske projekcije koriste i geodezija, geografija, astronomija, navigacija i druge znanosti.[1]
Kartografske projekcije najčešće se koriste za izradu karata objekata oblika sfere ili elipsoida, kao što je Zemlja,[1] no u matematici je kartografska projekcija može biti funkcija koja preslikava površinu bilo koje neprekidne zakrivljene plohe na ravninu.
Položaj točke na sfernim i elipsoidnim objektima precizno i jednoznačno izražavamo pomoću koordinata. Tipično se za to koriste tzv. zemljopisne koordinate, koje si možemo predočiti pomoću mreže meridijana i paralela (vidi i sferni koordinatni sustav). Projekcija je, matematički gledano, poveznica između položaja točaka u koordinatnom sustavu projiciranog objekta, i položaja u koordinatnom sustavu ravnine. To se obično zapisuje jednadžbom:
gdje su φ i λ zemljopisne koordinate na projiciranom tijelu, a x i y Kartezijeve koordinate u ravnini. Projekcija mreže meridijana i paralela na ravninu zove se osnovna kartografska projekcija.[1]
Vrste projekcija
Theorema egregium Carla Friedricha Gaussa dokazuje da je nemoguće projicirati površinu zakrivljene plohe, kao što je Zemljina površina, na ravninu bez izobličenja. Posljedica tog teorema je da sve projekcije izobličuju bar neko svojstvo objekata na početnom tijelu. Ako projiciramo samo mali djelić početnog tijela, izobličenja mogu biti zanemarivo mala, te je manje važno koju projekciju koristimo. No u suprotnom slučaju, kao pri izradi karata velikih država ili čitavih kontinenata na Zemlji, izobličenja postaju velika. Pri izradi karata najčešće želimo sačuvati duljine, ploštine i kutove s početnog tijela, no možemo samo jedno od toga istovremeno. Tako i projekcije redom dijelimo na:[1]
- ekvidistantne, koje čuvaju duljine
- ekvivalentne, koje čuvaju ploštine
- konformne, koje čuvaju kutove, dakle i oblike na površini početnog tijela
- uvjetne, koje čuvaju neko drugo svojstvo
Primjerice, Mercatorova projekcija je konformna i korisna je jer čuva kutove i kurseve, zbog čega je korisna u navigaciji, a i u čestoj je upotrebi na računalnim kartama jer čuva oblike zemalja, otoka i kontinenata. Međutim, Mercatorova projekcija ima velika izobličenja duljina i ploština pri velikoj geografskoj širini. Tako je Grenland prikazan otprilike jednake veličine kao Afrika, dok u stvarnosti Afrika ima 14 puta veću površinu od Grenlanda.
Za predočenje izobličenja koje čini projekcija koristi se Tissotova indikatrisa.
Podjela po razvojnoj površini
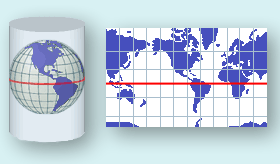
Neke projekcije mogu se izraziti i kao projekcije u matematičkom smislu na razvojne plohe. Razvojne plohe su plohe koje možemo bez savijanja razviti u ravninu, te time dobiti kartu. To su, primjerice, površina valjka ili stošca. Sfera je primjer površine koja nije razvojna.
- cilindrične, na površinu valjka
- konusne, na površinu stošca
- azimutne, na ravninu
Ova podjela ne pokriva sve kartografske projekcije.
Poznate projekcije
Neke projekcije nazvane su po izumiteljima, dok su druge ime dobile po svojstvu koje čuvaju ili po znanstvenom području primjene.[1]
- Cassinijeva projekcija
- Fullerova projekcija (dimaksijska projekcija, karta dymaxion)
- Ekvirektangularna projekcija
- Gall-Petersova projekcija s rezolucijom koja se odnosi na uporabu pravokutnih karata svijeta
- Gnomonska projekcija
- Lambertova konformna konusna projekcija (široko korištena u avijaciji)
- Mercatorova projekcija
- Mollweideova projekcija
- Robinsonova projekcija
- Transverzalna Mercatorova projekcija
- Winkelova trostruka projekcija
