Prostorni kut

Grafički prikaz 1 steradijana. Kugla ima polumjer r, koji presjeca isječak plohe kugle površine A = r². Kut kružnog isječka je θ = A/r² ili θ = 1. Cijela sfera ima 4π sr ≈ 12,56637 sr.

Presjek steradijana: (1) stožac, (2) kuglin odsječak.

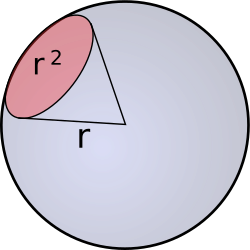
Prostorni kut (oznaka Ω ili ω) je fizikalna veličina koja opisuje dimenziju vidokruga iz perspektive neke točke u prostoru. Neka je sfera polumjera r centrirana u točki zrenja. Tada ako se u vidokrugu kojim je definiran dani prostorni kut nalazi dio površine sfere koji ima ploštinu A, prostorni kut definiramo kao omjer

$\Omega ={\frac {A}{r^{2}}}$

Mjerna jedinica prostornog kuta je steradijan (sr).

Steradijan

Podrobniji članak o temi: Steradijan

Steradijan (oznaka: sr) je jedinica za prostorni kut. Prostorni kut čiji se vrh nalazi u središtu kugle, a na sferi omeđuje površinu jednaku kvadratu polumjera kugle, iznosi jedan steradijan. Steradijan je SI izvedena jedinica. To je bezdimenzionalna jedinica, jer 1 sr = m² · m⁻² = 1, ali u praksi je prikladno koristiti oznaku sr, umjesto 1 ili ničega.

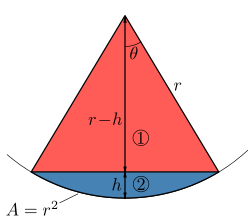
Po definiciji je r – polumjer kugle, h – visina kuglinog odsječka, θ – kut kružnog isječka. Budući je po definiciji steradijana A = r², to odgovara površini kuglinog isječka (A = 2πrh), iz čega dobijamo h/r = 1/(2π). Kut kružnog isječka iznosi:

${\begin{aligned}\theta &=\arccos \left({\frac {r-h}{r}}\right)\\&=\arccos \left(1-{\frac {h}{r}}\right)\\&=\arccos \left(1-{\frac {1}{2\pi }}\right)\approx 0,572\,{\text{rad}}{\mbox{ ili }}32,77^{\circ }\end{aligned}}$

Ili vrijedi 2θ ≈ 1,144 rad ili 65,54°.

Budući je površina sfere 4πr², to znači da prostorni kut koji pokriva čitav prostor ima 4π sr ≈ 12,56637 sr.