Injektivna funkcija: razlika između inačica
Prijeđi na navigaciju
Prijeđi na pretraživanje
Bot: Automatski unos stranica |
m brisanje nepotrebnog teksta Oznaka: poveznice na razdvojbe |
||
| Redak 1: | Redak 1: | ||
[[Datoteka:Injection.svg|okvir|Right|Na slici vidimo da su se svi elementi iz X preslikali u različite elemente u Y]] | |||
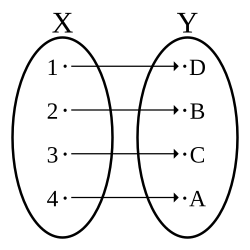
[[Datoteka:Bijection.svg|okvir|Right|Funkcija koja je [[injekcija]] i [[surjekcija]], odnosno, ona je [[bijekcija]]]] | [[Datoteka:Bijection.svg|okvir|Right|Funkcija koja je [[injekcija]] i [[surjekcija]], odnosno, ona je [[bijekcija]]]] | ||
Posljednja izmjena od 8. ožujak 2022. u 11:45
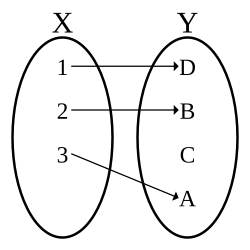
Za funkciju kažemo da je injektivna funkcija ili samo injekcija ako ne postoje dva različita elementa domene, a koji se preslikavaju u neki isti element iz kodomene.
To znači da se svi elementi iz domene preslikavaju u međusobno različite elemente iz kodomene (funkcija ne "lijepi" različite elemente u isti).
Definicija
Zapisano simboličkom logikom, je injektivna ako vrijedi:
što je logički ekvivalentno tvrdnji:
Vidi još i :
![]() Nedovršeni članak Injektivna funkcija koji govori o matematici treba dopuniti. Dopunite ga prema pravilima uređivanja Hrvatske internetske enciklopedije.
Nedovršeni članak Injektivna funkcija koji govori o matematici treba dopuniti. Dopunite ga prema pravilima uređivanja Hrvatske internetske enciklopedije.


