Graf funkcije

Graf funkcije f(x) = x⁴ − 4^x na intervalu [-2,+3]. Također su prikazana i dva realna rješenja i globalni minimum na istom intervalu.

U matematici, graf funkcije f je skup svih uređenih parova (x, f(x)). Ako je ulazna funkcija x skalarna, njezin graf (krivulja) ima dvije dimenzije. Ako je zavisna varijabla x uređeni par (x₁, x₂) realnih brojeva, graf (površina) je skup svih uređenih trojki (x₁, x₂, f(x₁, x₂)).

U znanosti, inženjerstvu, tehnologiji, financijama i drugim područjima, grafovi se koriste za različite svrhe. U najjednostavnijem slučaju jedna se varijabla grafički prikazuje kao funkcija druge varijable, obično pomoću pravokutnih osi.

U poljima moderne matematike, poput teorije skupova, funkcija i njezin graf označavaju isti koncept.

Vrste grafova

Ovisno o najvećoj potenciji nepoznanice, postoji više vrsta grafova:

Objašnjenje grafa linearne funkcije.

Prikaz osječka pravca na objema koordinatnim osima

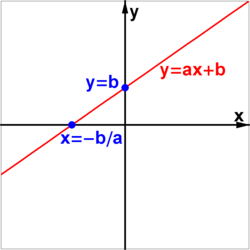
Linearna funkcija

Funkciju $f:R\rightarrow R$ zadanu formulom $f(x)=kx+l$, zovemo linearna funkcija, a graf joj iskazujemo pravcem. Varijabla l označava sjecište grafa s y-osi, dok varijabla k izražava nagib pravca. Nagib k može se izračunati kao ${\frac {\Delta y}{\Delta x}}$ili kao tangens kuta pravca nad x-osi. Derivacija linearne funkcije iskazana je njenim nagibom.

Kvadratna funkcija

Ako pak funkcija ima oblik $f(x)=ax^{2}+bx+c$, zovemo ju kvadratna funkcija. Ako je funkcija oblika $f(x)=x^{2}(ax^{2}+b)+c$, odnosno jednostavnije, $f(x)=ax^{4}+bx^{2}+c$, tad se naziva bikvadratna funkcija. Funkcije ovog oblika su parabole, čija realna rješenja (nultočke) x₁ i x₂ nakon izjednačavanja s nulom daju odsječke grafa na x-osi, sukladno formuli ${\textstyle _{1}x_{2}={\frac {-b\pm {\sqrt {b^{2}-4ac}}}{2a}}}$. Tjeme kvadratne funkcije možemo dobiti općom formulom ${\textstyle (x_{0}={\frac {x_{1}+x_{2}}{2}},f(x_{0}))}$, ili jednostavnije $({\frac {-b}{2a}},{\frac {4ac-b^{2}}{4a}})$, gdje su a, b i c koeficijenti kvadratne funkcije. Ukoliko je varijabla a pozitivna, funkcija prvo pada pa raste, a ako je negativna događa se obrnuto. S obzirom da je najveća potencija funkcije parna (2), funkcija počinje i završava na istoj "strani" grafa. Derivacija kvadratne funkcije je pravac 2ax+b.

Diskriminanta funkcije

Diskriminanta je vrijednost opisana formulom $D=b^{2}-4ac$, gdje su a, b i c koeficijenti kvadratne jednadžbe, koja nam govori koliko rješenja ima određena kvadratna jednadžba. Ako je vrijednost diskriminante veća od nule, funkcija tad dodiruje x-os u barem dvije točke, a njezina jednadžba ima dva realna rješenja. Ako je D=0, tjeme funkcije leži na x-osi (dodiruje x-os u jednoj točki), a njezina jednadžba ima jedno realno i jedno kompleksno rješenje. Ako je diskriminanta manja od nule, funkcija ne dodiruje x-os, i ima dva kompleksna rješenja.

Funkcije višeg reda

Podrobniji članak o temi: Polinom

Funkcija oblika $f(x)=a_{n}x^{n}+a_{n-1}x^{n-1}+...+a_{2}x^{2}+a_{1}x+a_{0}$ naziva se polinom n-tog reda/stupnja. Svaki se takav polinom može napisati u obliku produkta: $f(x)=a_{n}(x-x_{1})(x-x_{1})(x-x_{2})\cdot ...\cdot (x-x_{n})$, gdje su x₁, x₂, ... x_n sva rješenja jednadžbe f(x)=0. Racionalna funkcija zadana je formulom ${\textstyle f(x)={\frac {g(x)}{h(x)}}}$, gdje su g i h polinomi (h ne smije biti nula).

Oblici jednadžbe pravca

Izvori

1. PREUSMJERI Predložak:Izvori

Vanjske poveznice

• Graph of function, derivative and antiderivative plotter
• Weisstein, Eric W. "Function Graph." From MathWorld—A Wolfram Web Resource.
• Graphing slope-intercept - simulacija povezanosti funkcije i izgleda grafa, PhET, Sveučilište u Coloradu