Skalarni umnožak

Datoteka:Scalarproduct.gif

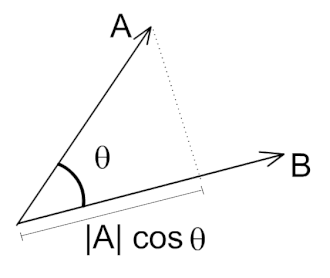
Skalarni umnožak dva vektora je definiran kao umnožak iznosa (modula, duljine, intenziteta) prvog i drugog vektora i kosinusa kuta između njih. Dobiveni je rezultat skalar.

${\vec {a}}\cdot {\vec {b}}={\vec {b}}\cdot {\vec {a}}=\left|{\vec {a}}\right|\left|{\vec {b}}\right|\cos \phi$

Skalarni umnožak vektora sa samim sobom daje kvadrat njegovog iznosa, jer je u tom slučaju kosinus 0° jednak 1. Skalarni umnožak vektora koji su pod pravim kutom (90°) jednak je 0, jer je kosinus pravog kuta 0.

Skalarni umnožak je komutativan, distributivan i linearan.

Definicija i primjer

Definicija skalarnog umnoška vektora a = [a₁, a₂, … , a_n] i vektora b = [b₁, b₂, … , b_n] :

Obrada nije uspjela. (MathML sa SVG ili PNG za rezervu (preporučljivo za moderne preglednike i alate za pristupačnost): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mathbf{a}\cdot \mathbf{b} = \sum_{i=1}^n a_ib_i = a_1b_1 + a_2b_2 + \cdots + a_nb_n }

• gdje Σ označuje zbrajanje po komponentama.

Primjer skalarnog množenja na trodimenzionalnom vektoru [1, 3, −5] i [4, −2, −1]:

Obrada nije uspjela. (MathML sa SVG ili PNG za rezervu (preporučljivo za moderne preglednike i alate za pristupačnost): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \begin{bmatrix}1&3&-5\end{bmatrix} \cdot \begin{bmatrix}4&-2&-1\end{bmatrix} = (1)(4) + (3)(-2) + (-5)(-1) = 3.}

Geometrijska interpretacija

S obzirom da znamo da je skalarni umnožak i umnožak sa kutom između dva vektora, možemo inverznom operacijom izračunati i kut.

$\mathbf {a} \cdot \mathbf {b} =|\mathbf {a} |\,|\mathbf {b} |\cos \theta \,$ Obrada nije uspjela. (MathML sa SVG ili PNG za rezervu (preporučljivo za moderne preglednike i alate za pristupačnost): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \Longrightarrow} Obrada nije uspjela. (Conversion error. Server ("https://wikimedia.org/api/rest_") reported: "Cannot get mml. Server problem."): {\displaystyle \theta =\arccos \left({\frac {\mathbf {a} \cdot \mathbf {b} }{|\mathbf {a} ||\mathbf {b} |}}\right).}

Vidjeti također

• Vektorski umnožak