Sferno zrcalo
Sferno zrcalo je dio kugline kalote koji odbija zrake svjetlosti s unutarnje ili s vanjske strane. Ono sferno zrcalo koje je s nutarnje strane fino polirano i na toj strani odbija zrake svjetlosti zove se udubljeno ili konkavno zrcalo. Ako je zrcalo s vanjske strane polirano i s te strane odbija zrake svjetlosti, onda je to ispupčeno ili konveksno zrcalo.
Udubljeno ili konkavno zrcalo
Geometrijsko središte kugline plohe ili sfere je središte zakrivljenosti zrcala, a polumjer te kugle je polumjer zakrivljenosti zrcala r. Točka u sredini zrcala je tjeme zrcala, a pravac koji spaja tjeme i središte zove se optička os zrcala. Kut što ga u središtu zakrivljenosti zrcala čine polumjeri povučeni prema rubu zrcala zove se kut otvora ili apertura zrcala.
Možemo si zamisliti da je udubljeno zrcalo sastavljeno od niza ravnih zrcala koja su to više nagnuta prema optičkoj osi što se nalaze dalje od nje. Zato su kutovi upadanja paralelnih zraka to veći što se ta ravna zrcala nalaze dalje od optičke osi, pa će se zrake odbijati sve strmije po zakonu refleksije. Sve reflektirane zrake prolazit će kroz jednu točku koja se zove žarište ili fokus F. Udaljenost žarišta od tjemena zrcala zove se žarišna daljina f. Ona je jednaka polovini polumjera zakrivljenosti, to jest:
- [math]\displaystyle{ f = \frac{r}{2} }[/math]
Ako os udubljenog zrcala okrenemo prema Suncu, razvit će se u žarištu toliko topline da će se moći zapaliti šibica.
Kod većih kutova otvora zrcala paralelne zrake neće se više nakon refleksije sastati u jednoj točki. Zrake više udaljene od optičke osi sjeći će se bliže tjemenu, a zrake bliže optičkoj osi sjeći će se dalje od tjemena zrcala. Ta se površina zove katakaustička ploha, koju možemo pokazati pomoću jednog prstena koji leži na svijetloj podlozi ako na njega padaju Sunčeve zrake. Pogreška udubljenog ili konkavnog zrcala da mu se krajnje zrake ne sijeku u žarištu zove se sferna aberacija. Tu pogrešku nema parabolično udubljeno zrcalo. To je zbog svojstva da radijvektor, to jest pravac povučen iz žarišta do bilo koje točke parabole i pravac povučen iz iste točke paralelno s njezinom osi zatvara s normalom parabole u toj točki uvijek isti kut. Zato su astronomska zrcala uvijek parabolična.
Udubljeno ili konkavno zrcalo ima to važno svojstvo da zrake koje izlaze iz jedne svijetle točke skuplja nakon refleksije ponovo u jednoj točki. Točka A’ je slika točke A. Povučemo li zraku paralelno s optičkom osi, ona će se reflektirati kroz žarište F. Zraka, koja prolazi kroz optičko središte reflektirat će se natrag u samu sebe. Sve ostale zrake koje izlaze iz svjetle točke A se nakon refleksije sijeku u točki A’.
Za razliku od ranije opisane virtualne (prividne) slike u ravnom zrcalu, ova slika koju možemo uhvatiti na zastoru je stvarna ili realna. Pomoću udubljenog ili konkavnog zrcala možemo dobiti stvarnu ili realnu sliku predmeta, te prividnu ili virtualnu. Slika može biti također uspravna ili obrnuta, povećana ili umanjena. Konstrukcijom dobijemo sliku predmeta tako da povučemo dvije zrake. Jednu od bilo koje točke predmeta paralelno s optičkom osi koja se reflektira paralelno s osi. Gdje se te dvije reflektirane zrake sijeku, tamo je slika točke predmeta.
Imamo slučaj kada je predmet izvan dvostruke žarišne daljine. Tada je slika obrnuta, umanjena i stvarna, a nalazi se između žarišta i središta. Imamo i drugi slučaj kada je predmet između žarišta i središta. Tada je slika obrnuta, uvećana i stvarna, a nalazi se izvan dvostruke žarišne daljine. U slučaju da je kada je predmet unutar žarišne daljine, slika je uspravna, uvećana ali prividna jer se nalazi izvan zrcala. Konstrukcijom dobijemo ovu sliku tako da crtamo zraku, paralelno s optičkom osi koja se reflektira kroz žarište, a zatim zraku koja kao da dolazi iz žarišta, pa se reflektira paralelno s osi. Produžimo li pravce tih zraka unatrag, dobit ćemo sliku predmeta u njihovu presjecištu.
Na osnovu obrazloženih slika može se zaključiti:
- kod udubljenog zrcala stvarna slika uvijek je obrnuta i to umanjena ili povećana, a prividna slika uvijek je povećana i uspravna;
- slika se odmiče od zrcala kada se predmet približava zrcalu.
Udubljena ili konkavna zrcala se upotrebljavaju kod brodskih, vojnih i automobilskih reflektora gdje se u njihovu žarištu nalazi električna žarulja, pa reflektor daje snažan paralelan pramen svjetlosnih zraka. [1]
Slike
| Položaj predmeta (S), žarište (F) |
Slika | Skica |
|---|---|---|
| [math]\displaystyle{ S\lt F }[/math] (predmet je unutar žarišne daljine) |
|
|
| [math]\displaystyle{ S=F }[/math] (predmet je u žarištu) |
|
|
| [math]\displaystyle{ F\lt S\lt 2F }[/math] (predmet je između žarišta i središte zakrivljenosti zrcala) |
|
|
| [math]\displaystyle{ S=2F }[/math] (predmet je u središtu zakrivljenosti zrcala) |
|
|
| [math]\displaystyle{ S\gt 2F }[/math] (predmet je izvan dvostruke žarišne daljine) |
|
|
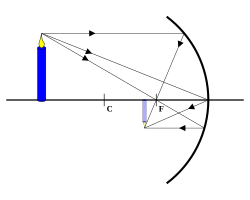
Ispupčeno ili konveksno zrcalo
Paralelne zrake koje padaju na takvo zrcalo, reflektiraju se kao da dolaze iz žarišta koje se nalazi iza zrcala. S ispupčenim ili konveksnim zrcalom možemo dobiti samo prividnu ili virtualnu, uspravnu i umanjenu sliku. Crtnjom se slika dobije tako da crtamo zraku od predmeta paralelnu s optičkom osi koja se odbija kao da dolazi iz žarišta, i zraku koja je upravljena prema žarištu i odbija se paralelno s optičkom osi.
Ispupčeno ili konveksno zrcalo služi vozačima da vide unatrag tko iza njih vozi, jer se na tom zrcalu reflektira mnogo predmeta.
Slika
| Položaj predmeta (S), žarište (F) |
Slika | Skica |
|---|---|---|
| [math]\displaystyle{ S\gt F,\ S=F,\ S\lt F }[/math] |
|
|
Jednadžba sfernog zrcala
Za relativno mali kut otvora zrcala i visinu predmeta AC možemo uzeti da točke L, M i N leže na istom pravcu. Pri tom je LM = AC = y = veličina predmeta, MN = A’C’ = y’ = veličina slike, MC = a = udaljenost predmeta od tjemena zrcala, MC’ = b = udaljenost slike od tjemena zrcala. Iz sličnosti trokuta može se izračunati:
- [math]\displaystyle{ \frac{y}{a - f} = \frac{y'}{f} }[/math]
pa je:
- [math]\displaystyle{ y \cdot f = {a - f} \cdot y' }[/math]
a odatle je:
- [math]\displaystyle{ \frac{y'}{y} = \frac{f}{a - f} }[/math]
Također se iz sličnosti trokuta može se izračunati:
- [math]\displaystyle{ \frac{y'}{b - f} = \frac{y}{f} }[/math]
pa je odatle:
- [math]\displaystyle{ y' \cdot f = {b - f} \cdot y }[/math]
a odatle:
- [math]\displaystyle{ \frac{y'}{y} = \frac{b - f}{f} }[/math]
Usporedimo li dobivene rezultate, dobivamo:
- [math]\displaystyle{ \frac{b - f}{f} = \frac{f}{a - f} }[/math]
a odatle:
- [math]\displaystyle{ \frac{1}{a} + \frac{1}{b} = \frac{1}{f} }[/math]
ili:
- [math]\displaystyle{ \frac{1}{a} + \frac{1}{b} = \frac{2}{r} }[/math]
To je jednadžba sfernog zrcala koju možemo riječima ovako izraziti: Zbroj recipročnih vrijednosti udaljenosti predmeta i slike od zrcala jednak je recipročnoj vrijednosti žarišne daljine. Iz te jednadžbe proizlazi:
- [math]\displaystyle{ f = \frac{a \cdot b}{a + b} }[/math]
Uvrstimo li ove vrijednost u izraz:
- [math]\displaystyle{ \frac{y'}{y} = \frac{f}{a - f} }[/math]
dobit ćemo izraz za povećanje slike, to jest omjer između veličine slike i veličine predmeta:
- [math]\displaystyle{ \frac{y'}{y} = \frac{b}{a} }[/math]
Taj izraz kazuje da se veličina slike odnosi prema veličini predmeta kao daljina slike prema daljini predmeta od zrcala.
Izvori
- ↑ Velimir Kruz: "Tehnička fizika za tehničke škole", "Školska knjiga" Zagreb, 1969.