Paradoks ljestava

Paradoks ljestava je misaoni pokus u posebnoj teoriji relativnosti u kojem dugačke ljestve gibajući se vodoravno brzinom bliskom brzini svjetlosti bivaju podložne kontrakciji dužine tako da mogu biti smještene u manju garažu.

Paradoks

Crtež 1a: Problem, 1. dio – dugačke ljestve kontrahirane duljine bivaju smještene u manju garažu.

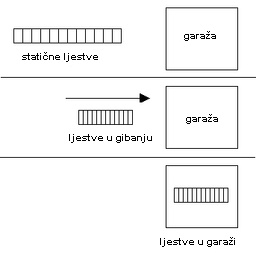
Dugačke ljestve gibajući se vodoravno brzinom bliskom brzini svjetlosti bivaju podložne kontrakciji dužine tako da mogu biti smještene u manju garažu.

Crtež 1b: Problem, 2. dio – kontrahirana duljina garaže premala je da se u nju smjeste ljestve iste duljine.

Zbog simetrije, može se argumentirati da je iz perspektive ljestava duljina garaže kontrahirana i zbog toga se ljestve uopće ne mogu smjestiti u nju.

Crtež 1c: Rješenje sa stajališta garaže: ljestve kontrahirane duljine ulaze i izlaze iz garaže s dvojim vratima.

Relativna simultanost

Rješenje ove dileme leži u činjenici da ono što jedan promatrač (tj. garaža) smatra simultanim ne korespondira s onim što drugi promatrač (tj. ljestve) smatra simultanim (relativna simultanost). Najjednostavniji način promatranja je zamišljanje garaže s dvojim vratima koja se otvaraju da bi uskladištila ljestve i propustila ljestve van na drugu stranu.

Crtež 1d: Rješenje sa stajališta ljestava: kontrahirana duljina garaže s dvojim vratima prolazi oko ljestava.

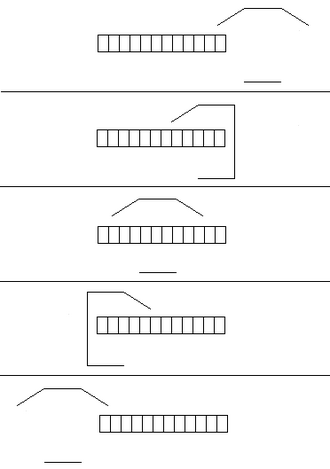
Iz perspektive ljestava događa se da se najprije jedna vrata zatvaraju i otvaraju i zatim, nakon što garaža prođe oko ljestava, druga vrata se zatvaraju i otvaraju.

Situacija je ilustrirana u donjem Minkowskijevom dijagramu. Dijagram je u referentnom okviru mirovanja garaže. Okomita plava traka pokazuje garažu u prostorvremenu, crvena vodoravna traka pokazuje ljestve u prostorvremenu. x i t os su osi prostora i vremena garaže, a [math]\displaystyle{ x' }[/math] i [math]\displaystyle{ t' }[/math] osi prostora i vremena ljestava. Ljestve se kreću brzinom [math]\displaystyle{ v=c\sqrt{1/2} }[/math] u pozitivnom smjeru osi x, stoga je [math]\displaystyle{ \gamma=\sqrt{2} }[/math]. Kako svjetlost putuje brzinom vrlo bliskoj jednoj stopi (=12 inča) u nanosekundi koristit ćemo te jedinice tako da je [math]\displaystyle{ c=1 }[/math]ft/ns. Garaža je mala, dugačka G=10 stopa, a ljestve su dugačke L=12 stopa. U referentnom okviru garaže, početak ljestava će dodirnuti stražnju stranu garaže u vremenu [math]\displaystyle{ t_A=G/v\approx14.14 }[/math] ns. To je prikazano kao događaj A na dijagramu. Svi pravci paralelni x osi garaže bit će simultani promatraču iz garaže, tako da će plava linija AB biti ono što će promatrač iz garaže vidjeti kao ljestve u vrijeme događaja A. Ljestve su smještene unutar garaže. Iz perspektive promatrača na ljestvama, crvena linija AC je ono što promatrač vidi kao ljestve – stražnji kraj ljestava je izvan garaže.

Crtež 1e: Minkowskijev dijagram paradoksa ljestava br. 1. Garaža je prikazana plavom bojom, ljestve crvenom. Dijagram je u referentnom okviru mirovanja garaže. Referentni okvir ljestava vrijedi za promatrača koji sjedi na prednjem kraju ljestava. Osi x i x' su dugačke po 5 stopa, a osi t i t' su po 5 ns .

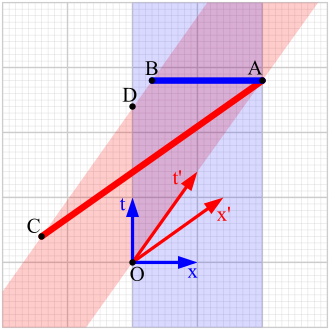
Koristeći jednodimenzionalne Lorentzove transformacije (vidjeti posebna relativnost) dobivamo:

Događaj	Okvir garaže	Okvir ljestava
[math]\displaystyle{ A\, }[/math]	[math]\displaystyle{ t_A=\frac{G}{v}\approx 14.14\, }[/math] ns [math]\displaystyle{ x_A=L=10\, }[/math] ft	[math]\displaystyle{ t^'_A=\frac{G}{\gamma v}=10\, }[/math] ns [math]\displaystyle{ x^'_A=0\, }[/math] ft
[math]\displaystyle{ B\, }[/math]	[math]\displaystyle{ t_B=t_A\approx14.14\, }[/math] ns [math]\displaystyle{ x_B=G-\frac{L}{\gamma}\approx 1.514\, }[/math] ft	[math]\displaystyle{ t^'_B=18.48\, }[/math] ns [math]\displaystyle{ x^'_B=-L=-12\, }[/math] ft
[math]\displaystyle{ C\, }[/math]	[math]\displaystyle{ t_C\approx2.142\, }[/math] ns [math]\displaystyle{ x_C\approx-6.971\, }[/math] ft	[math]\displaystyle{ t^'_C=10\, }[/math] ns [math]\displaystyle{ x^'_C=-12\, }[/math] ft
[math]\displaystyle{ D\, }[/math]	[math]\displaystyle{ t_D=12\, }[/math] ns [math]\displaystyle{ x_D=0\, }[/math] ft	[math]\displaystyle{ t^'_D=16.97\, }[/math] ns [math]\displaystyle{ x^'_D=-12\, }[/math] ft

Rješenje paradoksa

Ljestve kontrahirane uslijed ubrzanja tako da stanu u prostor kontrahirane duljine garaže.

Kada statična garaža obuhvati ljestve u gibanju, ono što se zatim događa je da 1) ljestve nastavljaju gibanje na drugu stranu izvan garaže (gornji primjer garaže s dvojim vratima) ili 2) ljestve u cijelosti stanu u garažu.

Promatrajući samo slijed, možemo reći da je svaka točka ljestava simultano u mirovanju sa stajališta garaže. Iz perspektive ljestava to ne može biti istina. Ljestve doživljavaju usporavanje točku po točku, dok konačno cijele ljestve ne usporavaju. Drugim riječima, ljestve se 'skraćuju' zbog vlastitog usporavanja ulazeći u inercijski referentni okvir garaže. Tako se iz obje perspektive ljestve mogu smjestiti u garažu. (Nakon toga, kako se više ne kreću relativno u odnosu na garažu, ljestve se mogu vratiti na originalnu duljinu, uzrokujući pri tome moguću štetu po sebe i garažu.)

Crtež 1 – Minkowskijev dijagram slučaja u kojem ljestve usporavaju duž svoje duljine, simultano u referentnom okviru garaže. Dok se to događa, promatrač iz referentnog okvira garaže vidi ljestve kao AB, ali promatrač iz referentnog okvira ljestava vidi ljestve kao AC. Kada stražnji kraj ljestava uđe u garažu u točki D, efekt usporavanja se još ne osjeća. U tom trenutku, za nekoga tko miruje u odnosu na stražnji kraj ljestava, prednji kraj ljestava bit će u točki E i vidjet će ljestve kao DE. Vidljivo je da ta dužina u referentnom okviru ljestava nije ista kao CA, duljina ljestava u mirovanju prije usporenja.