Lorentzov faktor

Lorentzov faktor kao funkcija brzine (u prirodnim jedinicama gdje je c = 1). Napominjemo da je za male brzine (manje od 0,1) γ približno jednak 1.

Lorentzove transformacije: prostorno-vremenske koordinate događaja, koje mjeri svaki promatrač u svom inercijalnom referentnom okviru (u standardnoj konfiguraciji), prikazane su u govornim oblacima.
Gore: okvir F' se kreće brzinom v duž osi x okvira F.
Dolje: okvir F kreće se brzinom −v duž osi x okvira F' .

Lijevo: promatrač u mirovanju mjeri vrijeme 2L/c između lokalnih događaja stvaranja svjetlosnog signala u A i dolaska u A. Desno: događaji prema promatraču koji se kreće lijevo od postavke: donje ogledalo A kada se signal stvara u trenutku t '= 0, gornje ogledalo B kad se signal reflektira u vremenu t ' = D/c, donje ogledalo A kad signal vraća u vremenu t '= 2D/c.

S obzirom na referentni sustav (plavi sat), u relativno ubrzanom crvenom satu vrijeme će teći sporije.

Vremenska dilatacija objašnjava zašto će dva radna sata izvještavati o različitim vremenima nakon različitih ubrzanja. Tako na primjer, vrijeme Međunarodne svemirske postaje ISS ide sporije, a zaostaje 0,007 sekundi za svakih šest mjeseci. Da bi GPS sateliti radili, oni se moraju prilagoditi sličnom savijanju svemirskog vremena kako bi se uskladili sa sustavima na Zemlji.

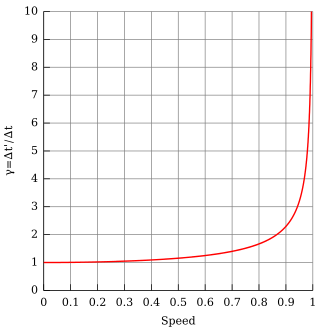
Lorentzov faktor (oznaka γ) je uobičajen pojam u posebnoj teoriji relativnosti, nazvan po nizozemskom fizičaru H. A. Lorentzu. Uobičajeno se određuje kao:

$\gamma ={\frac {1}{\sqrt {1-{\frac {v^{2}}{c^{2}}}}}}={\frac {1}{\sqrt {1-\beta ^{2}}}}$

gdje je: v - je relativna brzina između promatrača i objekta koji se kreće, c - brzina svjetlosti.

Lorentzove transformacije

Podrobniji članak o temi: Lorentzove transformacije

Lorentzove transformacije (po H. A. Lorentzu) su algebarske linearne relacije koje povezuju koordinate (x, y, z, t) nekoga fizičkog događaja u mirnome sustavu S (x, y, z, t) s pripadajućim koordinatama (x', y', z', t' ) u sustavu S' (x', y', z', t' ) koji se prema sustavu S giba uzduž osi x stalnom brzinom v. One se danas izvode, dokazuju i tumače iz dva postulata Einsteinove posebne teorije relativnosti (1905.):

1. postulata o konstantnosti brzine svjetlosti c u svim inercijskim sustavima bez obzira na brzinu sustava, izvora ili detektora svjetlosti, te
2. postulata kovarijantnosti da prirodni zakoni moraju imati isti oblik u svim inercijskim sustavima.

Polazeći od toga da svjetlosni signali (fotoni) putuju brzinom c u oba sustava i da se pravocrtna gibanja iz jednoga, kao takva, vide i u drugom sustavu i obratno (x = c∙t i x' = c∙t' ), kao i od načela relativnosti (zamjene uloge sustava S i S' i koordinata u njima), dobivaju se uz odgovarajući algebarski formalizam Lorentzove transformacije u obliku:

$t'=\gamma \cdot (t-{\frac {v}{c^{2}}}\cdot x)$

$x'=\gamma \cdot (x-v\cdot t)$

$y'=y$

$z'=z$

gdje se γ uobičajeno naziva Lorentzovim faktorom i vrijedi:

$\gamma ={\frac {1}{\sqrt {1-{\frac {v^{2}}{c^{2}}}}}}={\frac {1}{\sqrt {1-\beta ^{2}}}}$

Obratne (inverzne) transformacije dobivaju se zamjenom v s –v u već napisanim odnosima, na primjer:

$t=\gamma \cdot (t'+{\frac {v}{c^{2}}}\cdot x')$

$x=\gamma \cdot (x'+v\cdot t')$

$y=y'$

$z=z'$

Jedna je od temeljnih simetrija u fizici invarijantnost fizičkih zakona na Lorentzove transformacije (relativistička invarijantnost): jednadžbe fizike u svakom teoretskom pokušaju trebaju imati isti oblik u svim inercijskim sustavima. U modernoj fizici elementarnih čestica, invarijantnost se općenito postiže zapisom veličina i jednadžbi u 4-vektorskoj formulaciji, po uzoru na 4 koordinate prostor–vremena u posebnoj teoriji relativnosti.

Vremenska dilatacija

Podrobniji članak o temi: Vremenska dilatacija

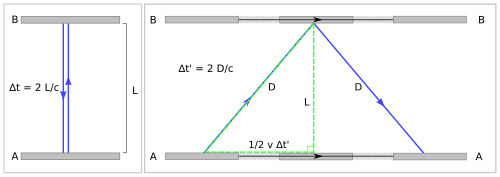
Na temelju svojih dvaju postulata Einstein je dobio jednadžbe identične Lorentzovim jednadžbama. Iz dobivenih jednadžbi izveo je Lorentzovu kontrakciju dužina i takozvanu dilataciju vremena, to jest rezultat da sat u gibanju ide polaganije ako ga usporedimo sa satovima sustava u kojem mjerimo. U sustavu koji se giba brzinom v sat će ići sporije t od isto takva sata t₀ u sustavu koji miruje. Taj se učinak naziva relativistička dilatacija vremena:

$t=\gamma \cdot t_{0}={\frac {t_{0}}{\sqrt {1-{\frac {v^{2}}{c^{2}}}}}}\,$

Kontrakcija dužine

Podrobniji članak o temi: Kontrakcija dužine

Druga je posljedica Lorentzovih transformacija kontrakcija dužine u smjeru gibanja. Njezina duljina L u sustavu mirovanja mjeri se kraćom od one vlastite L₀ u sustavu koji se giba brzinom v, po jednakosti:

$l={\frac {l_{0}}{\gamma }}=l_{0}\cdot {\sqrt {1-{\frac {v^{2}}{c^{2}}}}}$

gdje je: v - je relativna brzina između promatrača i objekta koji se kreće, c - brzina svjetlosti. Dimenzije nekoga tijela ne mogu se isto tako apsolutno odrediti kao ni vrijeme, jer i one ovise o stanju opažača. Einstein je izveo i teorem adicije brzina, kojim pokazuje da superpozicijom dviju brzina manjih od brzine svjetlosti opet izlazi brzina manja od brzine svjetlosti makar svaka od njih prelazi polovicu brzine svjetlosti. Dok su u Lorentza transformirane koordinate samo pomoćne varijable, u Einsteina su to prave fizičke veličine. Lorentzovo lokalno vrijeme, koje on razlikuje od pravoga vremena, u Einsteina postaje vrijeme dotičnoga sustava i ravnopravno je s vremenskim podatcima bilo kojega drugog sustava. Preračunavanje takvih podataka iz sustava u sustav sadržano je u jednadžbama transformacije. Time je karakteriziran možda najveći misaoni korak koji je učinio Einstein. Odbacio je koncepciju Newtonova apsolutnoga vremena označenu riječima: "Apsolutno, istinsko i matematičko vrijeme teče jednoliko po sebi i po svojoj prirodi i bez odnosa spram bilo čega izvanjskoga, a drugim se imenom zove trajanje". Jedan je od najdubljih rezultata Einsteinove pronicave analize spoznaja da istodobnost dvaju prostorno udaljenih događaja nije apsolutna činjenica, već da ovisi o tome u kojem se koordinatnom sustavu ti događaji promatraju.