Elektronska spektroskopija
Elektronska spektroskopija proučava spektroskopske prijelaze koji uključuju promjenu elektronske konfiguracije molekule. Pri tome elekroni u molekuli prelaze od jedne energijske razine u drugu.
Elektronska stanja i elektronski sustavi
Svako elektronsko stanje definirano je jedinstvenim rasporedom elektrona. Elektronsko stanje koje ima najnižu energiju, naziva se osnovno stanje. Ostala stanja, pobuđena stanja, obično jako kratko traju. Ta stanja, emitiranjem fotona ili vibracijskom relaksacijom, prelaze u osnovno stanje.
Osnovno stanje ozbačava se slovom X, a pobuđena stanja istog multipliciteta (istog broja nesparenih elektrona), velikim slovima A, B, C... Stanja drugačijeg multipliciteta, označavaju se malim slovima a, b, c...
Svako deformiranje molekule vodi povećanju potencijala. Potencijal za deformiranje molekule je drugačiji za svako elektronsko stanje, a svako elektronsko stanje, ovisno o potencijalu sadrži više vibracijskih stanja. Svako vibracijsko stanje sadrži više rotacijskih stanja. Skup svih vibracijskih i rotacijskih stanja jednog elektronskog stanja naziva se elektronski sustav.
Opći principi
Energija elektronskog prijelaza ovisi o: razlici energija elektronskih stanja, te o vibracijskim i rotacijskim stanjima u kojima se nalaizi početno i krajnje stanje:
- [math]\displaystyle{ \nu = T_e + G' \left( v' \right) + F' \left( J' \right) - G'' \left( v'' \right) - F'' \left( J'' \right) }[/math] (1)
gdje je je: [math]\displaystyle{ T_e }[/math] razlika u elektronskim stanjima, [math]\displaystyle{ G }[/math] vibracijski termovi, a [math]\displaystyle{ F }[/math] rotacijski termovi, [math]\displaystyle{ v }[/math] označava vibracijske kvantne brojeve, [math]\displaystyle{ J }[/math] rotacijske kvantne brojeve. Pojedine linije, koje odgovaraju prijelazu između stanja definiranih kvantnim brojevima: [math]\displaystyle{ v' }[/math], [math]\displaystyle{ v'' }[/math], [math]\displaystyle{ J' }[/math], [math]\displaystyle{ J'' }[/math], vidljivi su samo pomoću spektrofotometara visokog razlučivanja, a nazivaju se rovibronske linije. U običnim spektrofotometrima, rovibronske linije se stapaju u vibronske vrpce definirane vibracijskim kvantnim brojevima [math]\displaystyle{ v' }[/math] i [math]\displaystyle{ v'' }[/math].
Dvoatomne molekule
Dvoatomne molekule imaju samo jedan vibracijski normalni mod i samo dva rotacijska stupnja slobode (vidi: rotacijska spektroskopija i vibracijska spektroskopija), pa jednadžba (1) izgleda:
- [math]\displaystyle{ \nu = T_e + \omega'_e \left( v' + \frac{1}{2} \right) + B' J' \left( J'+1 \right) - \omega''_e \left( v'' + \frac{1}{2} \right) - B'' J'' \left( J'' + 1 \right) }[/math] (2)
Ukupni angularni moment molekule [math]\displaystyle{ \left( \overrightarrow{J} \right) }[/math] definira se kao vektorska suma rotacije molekule [math]\displaystyle{ \left( \overrightarrow{R} \right) }[/math], orbitalnog angularnog momenta [math]\displaystyle{ \left( \overrightarrow{L} \right) }[/math] i Spinskog angularnog momenta [math]\displaystyle{ \left( \overrightarrow{S} \right) }[/math]
- [math]\displaystyle{ \overrightarrow{J} = \overrightarrow{R} + \overrightarrow{L} + \overrightarrow{S} }[/math] (3)
Odgovarajuće komponente angularnih momenata duž internuklearne osi su: [math]\displaystyle{ \Lambda }[/math] za L, [math]\displaystyle{ \Sigma }[/math] za S i [math]\displaystyle{ \Omega }[/math] za J. Elektronska stanja se označavaju prema vijednostima [math]\displaystyle{ \Lambda }[/math]: [math]\displaystyle{ \Sigma }[/math] za [math]\displaystyle{ \Lambda =0 }[/math]; [math]\displaystyle{ \Pi }[/math] za [math]\displaystyle{ \Lambda=1 }[/math]; [math]\displaystyle{ \Delta }[/math] za [math]\displaystyle{ \Lambda=2 }[/math]; [math]\displaystyle{ \Phi }[/math] za [math]\displaystyle{ \Lambda=3 }[/math] itd. Stanja se označavaju s [math]\displaystyle{ ^{2S+1}\Lambda }[/math] sa + ili - u superskriptu ovisno o simetriji elektronskog stanja s obzirom na ravninu refleksije koja prolazi kroz jezgre atoma molekule. U slučaju homonuklearih dvoatomnih molekula, elektronska stanja se označavaju kao [math]\displaystyle{ ^{2S+1}\Lambda_x }[/math] gdje je x jednak g ili u ovisno da li je elektronsko stanje simetrično s obzirom na centar inverzije molekule (g; njemački gerade = simetrično) ili antisimetrično (u; njemački ungerade = nesimetrično).
Vjerojatnost prijelaza može se izračunati po formuli:
- [math]\displaystyle{ P \left( i,j \right) = \left\langle\Psi_i | \mu | \Psi_j \right\rangle }[/math] (4)
gdje je P vjerojatnost prijelaza između stanja i i j; [math]\displaystyle{ \Psi }[/math] je valna funkcija, a [math]\displaystyle{ \mu }[/math] je prijelazni dipolni moment. Formula vrijedi samo za spektroskopske prijelaze koji su posljedica promjene dipolnog momenta. Za prijlaze koji su posljedica promjene magnetskog momenta, kvadrupolnog momenta... itd. potrebno je primjeniti odgovarajući prijlazni moment, ali ti prijelazi su slabog intenziteta (prijelazni momenti su mali) i mogu se proučavati samo u rjetkim slučajevima. Vrijednost integrala u jednadžbi (4) ovisi o simetriji valnih funkcija i često kombinacija simatrija valnih funkcija rezultira s vrijednosti integrala 0. Za takve prijelaze se kože da su zabranjeni. Koji su prijelazi dozvoljeni, možemo saznati iz izbornih pravila, ne računajući integral (4).
[math]\displaystyle{ \Delta \Lambda = 0, \pm 1 }[/math] [math]\displaystyle{ \Delta S = 0 }[/math] (za teže molekule ovo pravilo nije striktno) [math]\displaystyle{ \Delta \Omega = 0, \pm 1 }[/math] [math]\displaystyle{ \Sigma^+-\Sigma^+ }[/math]; [math]\displaystyle{ \Sigma^-\Sigma^- }[/math]; [math]\displaystyle{ \Pi-\Sigma^+ }[/math]; [math]\displaystyle{ \Pi-\Sigma^- }[/math] [math]\displaystyle{ g - u }[/math] (za homonuklearne molekule)
višeatomne molekule
Za razliku od dvoatomnih molekula, višeatomne molekule sadrže 3N-6 (linearne molekule 3N-5) vibracijskih stupnjeva slobode, pa su i spektri višeatomnih molekula puno kompleksniji od dvoatomnih. Jednadžba (1) sada ovisi o više vibracijskih brojeva [math]\displaystyle{ \left(v_1, v_2, v_3, ... \right) }[/math]:
[math]\displaystyle{ \nu = T_e + G' \left( v'_1, v'_2,... \right) - G'' \left( v''_1, v''_2,... \right) }[/math] (5)
Vibracijska izborna pravila za dozvoljene elektronske prijelaze su: [math]\displaystyle{ \Delta v = 0, \pm1, \pm2,... }[/math] za totalno simetrične vibracije i [math]\displaystyle{ \Delta v = 0, \pm2, \pm4, ... }[/math] za nesimetrične prijelaze.
Mogući prijelazi su između sljedećih orbitala:
| [math]\displaystyle{ \sigma - \sigma^* }[/math] |
| [math]\displaystyle{ \pi - \pi^* }[/math] |
| [math]\displaystyle{ n - \sigma^* }[/math] |
| [math]\displaystyle{ n-\pi^* }[/math] |
gdje su [math]\displaystyle{ \sigma }[/math] i [math]\displaystyle{ \pi }[/math] vezne orbitale, [math]\displaystyle{ n }[/math] nevezna orbitala, a [math]\displaystyle{ \sigma^* }[/math] i [math]\displaystyle{ \pi^* }[/math] su protuvezne orbitale.
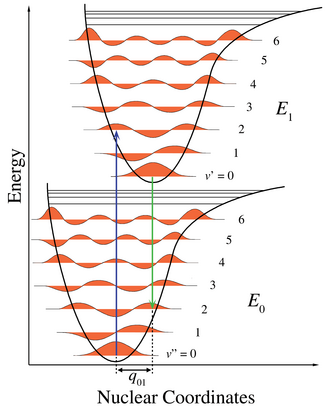
Elektronski prijelazi su jako brzi procesi, puno brži od vibracija molekula, pa će se molekula u pobuđenom stanju naći u onoj geometriji, u kojoj je bila prije pobuđivanja. Kako je molekula, prije pobuđivanja, redovito u osnovnom vibracijskom stanju, u pobuđenom stanju, će se naći u onom vibracijskom stanju, koje ima najveće preklapanje s osnovnim vibracijskim stanjem. Ovo pravilo se naziva Franck-Condonov princip.
Pobuđivanje elektrona u protuvezne orbitale vodi produljenju kemijskih veza u molekuli, što pobuđenu molekulu dovodi u vibracijski pobuđeno vibracijsko stanje, ili u ekstremnom slučaju do disocijacije molekule. U tom slučaju, u spektru je vidljiva široka vibronska vrpca, a u slučaju disocijacije, vrpca ili dio vrpce pokazuje kontinuum, tj izgleda kao glatka krivulja, bez strukture. U slučaju pobuđivanja elektrona u neveznu orbitalu, geometrija molekule se bitno ne mjenja, pa su vibracijske razine slične. Vrpca će biti relativno uska jer će sadržavati jednu ili mali broj vibronskih linija. Ukoliko dolazi do pobuđivanja iz protuvezne u veznu orbitalu, što je rjetki slučaj, kemijske veze u pobuđenom stanju se skraćuju, što dovodi do široke vrpce u spektru.
Ponekad se pobuđenje elektrona dogodi u orbitalu koja ne predstavlja vezno stanje, ili u dio orbitale koja je vezna, ali s tolikom vibracijskom energijom, da prelazi granicu disocijacije, pa dolazi do fotodisocijacije.