Descartesov list
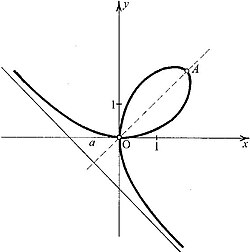
Descartesov list je ravninska algebarska krivulja trećeg reda u Kartezijevu koordinatnom sustavu koja je određena jednadžbom . Ova krivulja u ishodištu koordinatnoga sustava ima čvornu točku koja za tangente ima koordinatne osi i asimptotu . Tjeme krivulje, tj. sjecište njena dva luka koja se vide na slici, ima koordinate , a površina je petlje kao i površina dijela ravnine između krivulje i asimptote .[1]
Nazvana je prema slavnom francuskom matematičaru i filozofu Renéu Descartesu koji ju je proučavao 1638. i pronašao njezin oblik u I. kvadrantu, no pogrešno je mislio da se on ponavlja u ostala tri. Njezin točan oblik odredio je Huygens 1692. godine, odredivši pri tome i jednadžbu njene asimptote. Krivulja je postala poznata po svojoj povijesnoj ulozi u razvoju infinitezimalnog računa, a isto tako je Descartesov list povijesno važan i zbog činjenice da se u njegovim razmatranjima te krivulje prvi puta može vidjeti transformacija koordinata.[2] Treba ju distinkcirati od tzv. Descartesovog ovala.
Zanimljivo je da je Descartes izazvao Pierra de Fermata da nađe tangentu krivulje u svakoj točki zbog toga što je baš u to vrijeme Fermat otkrio metodu za pronalaženje tangenti. Fermat je riješio problem bez teškoća, što se ne može reći za Descartesa. Inače, nagib tangente u svakoj točki danas se lako može izračunati implicitnom diferencijacijom.
Lako se dobije da je formula za nagib tangente u svakoj točki .




