Analitička geometrija

Analitička geometrija je grana geometrije u kojoj se koriste algebarske metode prvenstveno linearne algebre da bi se riješili geometrijski problemi.

Metoda analitičke geometrije se koristi u svim primijenjenim znanostima, ali posebno unutar fizike, npr. za opis putanje planeta. Prvo se je analitička geometrija bavila pitanjima planeta i tzv. euklidskom geometrijom (prostornom geometrijom).

Koordinatni sustav

Osnova analitičke geometrije je korištenje koordinatnog sustava. Obično se koristi Kartezijev koordinatni sustav.

Analitička geometrija u R²

Koordinatni sustav i transformacije

Sa (x, y) označavaju se početne koordinate a sa (x', y') nove

Paralelno pomjeranje

Ako x₀, y₀ su koordinate koordinatnog početka u novom sistemu, onda vrijedi:

$x'=x-x_{0},\quad y'=y-y_{0}\,$

Rotacija

Ako se kut rotiranja $\alpha$ smatra pozitivnim( kut kojim se pozitivni x-os treba pomjerati da bi se podudarii s pozitivnim y-osom) onda su formule za transformaciju:

Obrada nije uspjela. (Conversion error. Server ("https://wikimedia.org/api/rest_") reported: "Cannot get mml. Server problem."): {\displaystyle x'=x\cos \alpha +y\sin \alpha \quad x=x'\cos \alpha -y'\sin \alpha \,}

Obrada nije uspjela. (Conversion error. Server ("https://wikimedia.org/api/rest_") reported: "Cannot get mml. Server problem."): {\displaystyle y'=y\cos \alpha -x\sin \alpha \quad y=x'\sin \alpha +y'\cos \alpha \,}

Udaljenost između dvije točke

Udaljenost između točaka (x₁, y₁) i (x₂, y₂) je:

${\sqrt {(x_{2}-x_{1})^{2}+(y_{2}-y_{1})^{2}}}\,$

Površina trokuta

Ako vrhovi trokuta imaju koordinate (x₁, y₁), (x₂, y₂) i (x₃, y₃), njihova površina je

Obrada nije uspjela. (Conversion error. Server ("https://wikimedia.org/api/rest_") reported: "Cannot get mml. Server problem."): {\displaystyle \pm T={\frac {1}{2}}{\begin{vmatrix}x_{1}&y_{1}&1\\x_{2}&y_{2}&1\\x_{3}&y_{3}&1\end{vmatrix}}=}

Obrada nije uspjela. (Conversion error. Server ("https://wikimedia.org/api/rest_") reported: "Cannot get mml. Server problem."): {\displaystyle ={\frac {1}{2}}[x_{1}(y_{2}-y_{3})+x_{2}(y_{3}-y_{1})+x_{3}(y_{1}-y_{2})]\,}

Da bi T bilo pozitivno, moraju točke (x₁,y₁), (x₂, y₂) i (x₃, y₃) slijediti jedna drugu u pozitivnom pravcu , tj. suprotno smjeru kretanja kazaljki na satu.

Dijeljenje udaljenosti

Ako se udaljenost između točaka (x₁, y₁) och (x₂, y₂), dijeli u odnosu na m/n koordinate će biti:

$x={\frac {mx_{2}+nx_{1}}{m+n}},\quad y={\frac {my_{2}+ny_{1}}{m+n}}\,$

Koeficijent kuta pravca

Neka $\alpha$ je kut koji pravac zatvara s x-osom. Ako pravac prolazi kroz točke (x₁, y₁) i (x₂,y₂) onda je oeficijent kuta pravca:

Obrada nije uspjela. (Conversion error. Server ("https://wikimedia.org/api/rest_") reported: "Cannot get mml. Server problem."): {\displaystyle \tan \alpha ={\frac {y_{2}-y_{1}}{x_{2}-x_{1}}};\quad x_{1}\neq x_{2}\,}

Jednadžba pravca

Jednadžba pravca je jednadžba prvog reda po x i y i opća formula je

Obrada nije uspjela. (Conversion error. Server ("https://wikimedia.org/api/rest_") reported: "Cannot get mml. Server problem."): {\displaystyle Ax+By+C=0\,}

Svaka jednadžba prvog reda predstavlja pravca.

$x=a\,$

znači pravac paralelan s y-osom i

Obrada nije uspjela. (Conversion error. Server ("https://wikimedia.org/api/rest_") reported: "Cannot get mml. Server problem."): {\displaystyle y=b\,}

pracac paralelan s är en linje parallell med x-osom.

Obrada nije uspjela. (Conversion error. Server ("https://wikimedia.org/api/rest_") reported: "Cannot get mml. Server problem."): {\displaystyle y=k\,x\,}

je pracac kroz koordinatni početak.

k-formula

Pravac se može napisati i u obliku

$y=k\,x+m\,$

ako je pravac paralelan s y-osom, tj. B är različit od nule. Ovdje je k koeficijent kuta pravca

Obrada nije uspjela. (Conversion error. Server ("https://wikimedia.org/api/rest_") reported: "Cannot get mml. Server problem."): {\displaystyle k=-{\frac {A}{B}},\quad m=-{\frac {C}{B}}\,}

i m y-koordinate dodira pravca s y-osom.

Presjek

Parametri presjecanja su točke presjeka pravaca x-ose i y-ose i pišu se

Obrada nije uspjela. (Conversion error. Server ("https://wikimedia.org/api/rest_") reported: "Cannot get mml. Server problem."): {\displaystyle {\frac {x}{a}}+{\frac {y}{b}}=1}

gdje a je x-koordinata za točku presjeka pravca s x-osom a b je y-koordinata za točku presjeka pravca s y-osom ili

$a=-{\frac {C}{A}},\quad b=-{\frac {C}{B}}\,$

Standardni oblik

Obrada nije uspjela. (Conversion error. Server ("https://wikimedia.org/api/rest_") reported: "Cannot get mml. Server problem."): {\displaystyle x\cos \alpha +y\sin \alpha -m=0\,}

je standardni oblik pravca. $\alpha$ och m bestäms ur

Obrada nije uspjela. (Conversion error. Server ("https://wikimedia.org/api/rest_") reported: "Cannot get mml. Server problem."): {\displaystyle m=-{\frac {C}{\sqrt {A^{2}+B^{2}}}},}

$\cos \alpha ={\frac {A}{\sqrt {A^{2}+B^{2}}}},\quad \sin \alpha ={\frac {B}{\sqrt {A^{2}+B^{2}}}}$

Znak kvadratnog korijena se bira tako da m bude pozitivno.

m je dužina normale iz koordinatnog početka do pravca i $\alpha$ je kut te normale s x-osom.

Udaljenost točke od pravca

Pravac napisan u standardom obliku

Obrada nije uspjela. (Conversion error. Server ("https://wikimedia.org/api/rest_") reported: "Cannot get mml. Server problem."): {\displaystyle x\cos \alpha +y\sin \alpha -m=0\,}

Onda je udaljenost točke P s koordinatama (x₁,y₁):

Obrada nije uspjela. (Conversion error. Server ("https://wikimedia.org/api/rest_") reported: "Cannot get mml. Server problem."): {\displaystyle p=\pm (x_{1}\cos \alpha +y_{1}\sin \alpha -m)\,}

gdje se znak + bira ako koordinatni početak i P leže na različitim stranama pravca.

Formula pravca kroz jednu točku

Jednadžba za pravac kroz točku (x₁, y₁) s kutnim koeficijentom k je

$y-y_{1}=k(x-x_{1})\,$

Formula pravca kroz dvije točke

Jednadžba za pravac kroz točke (x₁, y₁) i (x₂, y₂) je

Obrada nije uspjela. (Conversion error. Server ("https://wikimedia.org/api/rest_") reported: "Cannot get mml. Server problem."): {\displaystyle y-y_{1}={\frac {y_{2}-y_{1}}{x_{2}-x_{1}}}(x-x_{1})\,}

Kut između dva pravca

Ako su koeficijenti kuta pravca k₁ i k₂ kut između pravaca izračunava se kao:

Obrada nije uspjela. (Conversion error. Server ("https://wikimedia.org/api/rest_") reported: "Cannot get mml. Server problem."): {\displaystyle \tan \beta ={\frac {k_{2}-k_{1}}{1+k_{1}k_{2}}}\,}

Krivulje u ravni

Krivulja u ortogonalnom koordinatnom sustavu daje vezu između koordinata x i y i može se napisati kao funkcija.

Jednadžba krivulje se može napisati u eksplicitnom obliku

$y=f(x)\,$

u implicitnom obliku

Obrada nije uspjela. (Conversion error. Server ("https://wikimedia.org/api/rest_") reported: "Cannot get mml. Server problem."): {\displaystyle F(x,y)=0\,}

ili u parametarskom obliku

Obrada nije uspjela. (Conversion error. Server ("https://wikimedia.org/api/rest_") reported: "Cannot get mml. Server problem."): {\displaystyle x=x(t),\quad y=y(t)\,}

U polarnim koordinatama $(r,\psi )$ jednadžba krivulje je

Obrada nije uspjela. (Conversion error. Server ("https://wikimedia.org/api/rest_") reported: "Cannot get mml. Server problem."): {\displaystyle r=f(\psi )\,}

ili

Obrada nije uspjela. (Conversion error. Server ("https://wikimedia.org/api/rest_") reported: "Cannot get mml. Server problem."): {\displaystyle F(r,\psi )=0\,}

Tangenta

Koeficijent kuta za tengentu jednog pravca u pravokutnim koordinatima je jednak derivaciji funkcije u točki dodira:

$k={\frac {dy}{dx}}={\frac {d\,f(x)}{dx}}\,$

Obrada nije uspjela. (Conversion error. Server ("https://wikimedia.org/api/rest_") reported: "Cannot get mml. Server problem."): {\displaystyle k=-{\frac {\frac {\partial F}{\partial x}}{\frac {\partial F}{\partial y}}}\,\quad {\text{(implicitan oblik)}}}

Obrada nije uspjela. (Conversion error. Server ("https://wikimedia.org/api/rest_") reported: "Cannot get mml. Server problem."): {\displaystyle k={\frac {y'(t)}{x'(t)}}\,\quad {\text{(parametarski oblik)}}}

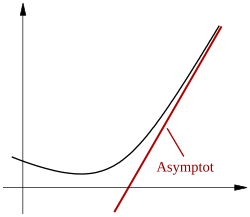
Asimptote

S asimptotom jedne krive misli se na pravac takav da razdaljina između pravca i točke na krivoj ide prema nuli gdje točka ide u beskonačnost. Ako se asimptota krivulje y = f(x) piše pomoću jednadžbe y = kx + m, onda se k i m određuju prema:

$k=\lim _{x\rightarrow \infty }{\frac {f(x)}{x}},\quad m=\lim _{x\rightarrow \infty }[f(x)-kx]\,$

Analitička geometrija u R³

Koordinatni sustav u R³

Koordinatni sustav

Koordinatni sustav u R³ koristi tri ravnine, obično okomite jedna na drugu. Točke presjeka se nazivaju x-, y- i z-os. Ove tri ravnine označavaju se po ulaznim osama kao xy-ravnina, yz-ravnina i xz-ravnina.

Pravokutne koordinate

Kosinus smjera

Koordinate točke P' (x, y, z) su okomita udaljenost do yz-, xz- i xy-ravni. Ako su Obrada nije uspjela. (Conversion error. Server ("https://wikimedia.org/api/rest_") reported: "Cannot get mml. Server problem."): {\displaystyle \alpha ,\,\beta ,\,\gamma \,} kutovi između vektora položaja duljine r i os onda je

Obrada nije uspjela. (Conversion error. Server ("https://wikimedia.org/api/rest_") reported: "Cannot get mml. Server problem."): {\displaystyle x=r\cos \alpha ,\quad y=r\cos \beta ,\quad z=r\cos \gamma }

gdje

$\cos \alpha ,\,\cos \beta ,\,\cos \gamma$

su kosinusi smjera označeni sa a, b i c za koje vrijedi

Obrada nije uspjela. (Conversion error. Server ("https://wikimedia.org/api/rest_") reported: "Cannot get mml. Server problem."): {\displaystyle a^{2}+b^{2}+c^{2}=1\,}

Kut između dva pravca

Ako imamo dva pravca, OA₁ sa kosinusima smjera a₁, b₁ i c₁ i OA₂ sa kosinusima smjera a₂, b₂ i c₂, onda vrijedi za kut $\theta$ između OA₁ i OA₂:

Obrada nije uspjela. (Conversion error. Server ("https://wikimedia.org/api/rest_") reported: "Cannot get mml. Server problem."): {\displaystyle \cos \theta =a_{1}a_{2}+b_{1}b_{2}+c_{1}c_{2}\,}

Rotacija koordinatnog sustava

S prijelazom iz pravkokutnog koordinatnog sustava (xyz) u jedan drugi (x'y'z') sa zajedničkim koordinatnim početkom ali različitim smjerovima osi i smjerovima kosinusa u xyz-osi označenim

za x'-os sa $(a',b',c')\,$

za y'-os sa Obrada nije uspjela. (Conversion error. Server ("https://wikimedia.org/api/rest_") reported: "Cannot get mml. Server problem."): {\displaystyle (a'',b'',c'')\,}

za z'-os sa Obrada nije uspjela. (Conversion error. Server ("https://wikimedia.org/api/rest_") reported: "Cannot get mml. Server problem."): {\displaystyle (a''',b''',c''')\,}

biće transformacije

${\begin{aligned}x&=a'x'+b'y'+c'z'\\y&=a''z'+b''y'+c''z'\\z&=a'''x'+b'''y'+c'''z'\end{aligned}}{\begin{aligned}\qquad x'&=a'x+a''y+a'''z\\y'&=b'x+b''y+b'''z\\z'&=c'x+c''y+c'''z\end{aligned}}$

Udaljenost između dvije točke

Udaljenost d između točaka (x₁, y₁, z₁) i (x₂, y₂, z₂) je

Obrada nije uspjela. (Conversion error. Server ("https://wikimedia.org/api/rest_") reported: "Cannot get mml. Server problem."): {\displaystyle d={\sqrt {(x_{2}-x_{1})^{2}+(y_{2}-y_{1})^{2}+(z_{2}-z_{1})^{2}}}\,}

Ako su a, b i c kosinusi pravca za pravac između dvije točke, onda se izračunavaju kao

Obrada nije uspjela. (Conversion error. Server ("https://wikimedia.org/api/rest_") reported: "Cannot get mml. Server problem."): {\displaystyle a={\frac {x_{2}-x_{1}}{d}},\quad b={\frac {y_{2}-y_{1}}{d}},\quad c={\frac {z_{2}-z_{1}}{d}},\,}

Ravnina u R³

Ako je (x₀, y₀, z₀) jedinični vektor do jedne točke u ravnini i (A, B, C) je okomit vektor na ravninu, može se jednadžba ravnine napisati kao skalrarni proizvod okimitog vektora i vektora (x - x₀, y - y₀, z - z₀):

$(A,B,C)(x-x_{0},y-y_{0},z-z_{0})=0\,$

što daje generalni oblik jednadžbe ravni kao

Obrada nije uspjela. (Conversion error. Server ("https://wikimedia.org/api/rest_") reported: "Cannot get mml. Server problem."): {\displaystyle Ax+By+Cz+D=0\,}

gdje je D

Obrada nije uspjela. (Conversion error. Server ("https://wikimedia.org/api/rest_") reported: "Cannot get mml. Server problem."): {\displaystyle -(Ax_{0}+By_{0}+Cz_{0})\,}

Jednadžba prvog reda predstavlja uvijek ravnunu. Cosinusi pravca za okomicu ravnine su En ekvation av första graden representerar alltid ett plan. Riktningscosinerna för planets normal är

${\frac {A}{\pm {\sqrt {A^{2}+B^{2}+C^{2})}}}},\quad {\frac {B}{\pm {\sqrt {A^{2}+B^{2}+C^{2})}}}},\quad {\frac {C}{\pm {\sqrt {A^{2}+B^{2}+C^{2})}}}},\,$

Znak pred korijenom se izabire tako da je

Obrada nije uspjela. (Conversion error. Server ("https://wikimedia.org/api/rest_") reported: "Cannot get mml. Server problem."): {\displaystyle {\frac {D}{\pm {\sqrt {A^{2}+B^{2}+C^{2})}}}}\,} uvijek pozitivan. Na taj način je okomica usmjerena prema ravninoj "pozitivnoj" strani.

Okomiti oblik

Dijeljenjem sa

Obrada nije uspjela. (Conversion error. Server ("https://wikimedia.org/api/rest_") reported: "Cannot get mml. Server problem."): {\displaystyle \pm {\sqrt {A^{2}+B^{2}+C^{2})}}\,}

dobijemo jednadžbu ravni u okomitom obliku

$x\cos \alpha +y\cos \beta +z\cos \gamma =p\,$

gdje suObrada nije uspjela. (Conversion error. Server ("https://wikimedia.org/api/rest_") reported: "Cannot get mml. Server problem."): {\displaystyle \alpha ,\beta ,\gamma } kutevi koje okomica na ravac čini s koordinatnim osama a p je udaljenost okomice od koordinatnog početka pa do ravnine.

Vektorski oblik

Pogreška pri izradbi sličice:

Jednadžba ravni s okomitim vektorom n, datom točkom r₀ i r kao jediničnim vektorim za proizvoljnu točku (x, y, z) u ravnini je

Obrada nije uspjela. (Conversion error. Server ("https://wikimedia.org/api/rest_") reported: "Cannot get mml. Server problem."): {\displaystyle (\mathbf {r} -\mathbf {r} _{0})\mathbf {n} =0\,}

Udaljenost točke od ravnine

Koordinate točke se pišu u okomitom obliku ravnine

$x\cos \alpha +y\cos \beta +z\cos \gamma -p=0\,$

a udaljenost je onda jednaka lijevoj strani jednadžbe sa predznakom '-' ako točka i koordinatni početak se nalaze na istoj strani ravnine, inače sa predznakom '+'.

Primjer:

Izračunati udaljenost od točke (1, -3, 2) do ravnine

Obrada nije uspjela. (Conversion error. Server ("https://wikimedia.org/api/rest_") reported: "Cannot get mml. Server problem."): {\displaystyle x+2y-2z+6=0\,}

Jednadžba ravnine u okomitom obliku

Obrada nije uspjela. (Conversion error. Server ("https://wikimedia.org/api/rest_") reported: "Cannot get mml. Server problem."): {\displaystyle {\frac {x+2y-2z+6}{-3}}=0;\quad d={\frac {1-3\cdot 2-2\cdot 2+6}{-3}}=1\,}

Kut između dvije ravnine

Kut $\omega$ između dvije ravnine

$A_{1}x+B_{1}y+C_{1}z+D_{1}=0\,$

Obrada nije uspjela. (Conversion error. Server ("https://wikimedia.org/api/rest_") reported: "Cannot get mml. Server problem."): {\displaystyle A_{2}x+B_{2}y+C_{2}z+D_{2}=0\,}

izračunava se pomoću jednadžbe

Obrada nije uspjela. (Conversion error. Server ("https://wikimedia.org/api/rest_") reported: "Cannot get mml. Server problem."): {\displaystyle \cos \omega ={\frac {A_{1}A_{2}+B_{1}B_{2}+C_{1}C_{2}}{{\sqrt {A_{1}^{2}+B_{1}^{2}+C_{1}^{2}}}{\sqrt {A_{2}^{2}+B_{2}^{2}+C_{2}^{2}}}}}\,}

Ako su okomiti vektori na ravninu poznati može se skalarni proizvod okomitih vektora upotrijebiti da bi se izračunao kut između ravnine:

$\cos \omega ={\frac {\mathbf {n} _{1}\mathbf {n} _{2}}{|\mathbf {n} _{1}||\mathbf {n} _{2}|}}\,$

Pravac

Pogreška pri izradbi sličice:

Pravac se može smatrati presjekom između dvije ravnine i može se napisati uz pomoć jednadžbi prvog reda

$A_{1}x+B_{1}y+C_{1}z+D_{1}=0\,$

Obrada nije uspjela. (Conversion error. Server ("https://wikimedia.org/api/rest_") reported: "Cannot get mml. Server problem."): {\displaystyle A_{2}x+B_{2}y+C_{2}z+D_{2}=0\,}

Pravac se može napisati pomoću točke P = (x₀, y₀, z₀) na pravcu i vektora pravca u:

U parametarskom obliku vrijedi za jednu točku (x, y, z) na pravoj liniji:

$(x,y,z)=(x_{0},y_{0},z_{0})+\lambda (a,b,c)\,$

ili

Obrada nije uspjela. (Conversion error. Server ("https://wikimedia.org/api/rest_") reported: "Cannot get mml. Server problem."): {\displaystyle x=x_{0}+a\lambda \,}

Obrada nije uspjela. (Conversion error. Server ("https://wikimedia.org/api/rest_") reported: "Cannot get mml. Server problem."): {\displaystyle y=y_{0}+b\lambda \,}

$z=z_{0}+c\lambda \,$

gdje su a, b i c koeficijenti pravca, ili poslije eliminiranja parametara

Obrada nije uspjela. (Conversion error. Server ("https://wikimedia.org/api/rest_") reported: "Cannot get mml. Server problem."): {\displaystyle {\frac {x-x_{0}}{a}}={\frac {y-y_{0}}{b}}={\frac {z-z_{0}}{c}}\,}

U vektorskom obliku jednadžba pravca se može napisati kao

Obrada nije uspjela. (Conversion error. Server ("https://wikimedia.org/api/rest_") reported: "Cannot get mml. Server problem."): {\displaystyle \mathbf {r} =\mathbf {r} _{0}+t\mathbf {u} \,}

Krive linije u R³

Kriva linija u R³ može nastati na više načina:

Kao presjekk dvije površine:

$F_{1}(x,y,z)=0\quad F_{2}(x,y,z)=0\,$

U parametarskom obliku:

Obrada nije uspjela. (Conversion error. Server ("https://wikimedia.org/api/rest_") reported: "Cannot get mml. Server problem."): {\displaystyle x=x(t)\quad y=y(t)\quad z=z(t)\,}

U vektorskom obliku:

Obrada nije uspjela. (Conversion error. Server ("https://wikimedia.org/api/rest_") reported: "Cannot get mml. Server problem."): {\displaystyle \mathbf {r} =x(t)\mathbf {i} +y(t)\mathbf {j} +z(t)\mathbf {k} \,}

Primjer:

Pogreška pri izradbi sličice:

Uvrnuta kriva linija se može napisati u parametarskom obliku kao

$x=r\cos(t)\quad y=r\sin(t)\quad z=kt\,$

Dužina luka

Dužina luka na krivoj liniji je

Obrada nije uspjela. (Conversion error. Server ("https://wikimedia.org/api/rest_") reported: "Cannot get mml. Server problem."): {\displaystyle ds={\sqrt {dx^{2}+dy^{2}+dz^{2}}}\,}

Dužina luka između t₀ i t je

Obrada nije uspjela. (Conversion error. Server ("https://wikimedia.org/api/rest_") reported: "Cannot get mml. Server problem."): {\displaystyle s=\int _{t_{0}}^{t}{\sqrt {x'(t)^{2}+y'(t)^{2}+z'(t)^{2}}}dt\,}

Tangenta

Jednadžba tangente u vektorskom obliku je

$\mathbf {t} =\left({\frac {d\mathbf {r} }{ds}}\right)_{0},\quad \mathbf {r} =\mathbf {r_{0}} +\lambda \left({\frac {d\mathbf {r} }{ds}}\right)_{0}\,$

Okomita ravan

Jednadžba u vektorskom obliku za okomitu ravninu u točki s je

Obrada nije uspjela. (Conversion error. Server ("https://wikimedia.org/api/rest_") reported: "Cannot get mml. Server problem."): {\displaystyle (\mathbf {r} -\mathbf {r_{0}} )\left({\frac {d\mathbf {r} }{ds}}\right)_{0}=0\,}

Dodirna ravnina

U točki na krivoj liniji u R³ može se općenito dodati nebrojeno mnogo tangentnih ravni krivulji. Tangentna ravnina koja je kao najbliža naslonjena na krivu liniju se naziva dodirna ravnina i ima jednadžbu

Obrada nije uspjela. (Conversion error. Server ("https://wikimedia.org/api/rest_") reported: "Cannot get mml. Server problem."): {\displaystyle A(x-x_{0})+B(y-y_{0})+C(z-z_{0})=0\,}

gdje se A, B i C izračunavaju iz formula

$A=y'(s)z''(s)-z'(s)y''(s)\,$

Obrada nije uspjela. (Conversion error. Server ("https://wikimedia.org/api/rest_") reported: "Cannot get mml. Server problem."): {\displaystyle B=z'(s)x''(s)-x'(s)z''(s)\,}

Obrada nije uspjela. (Conversion error. Server ("https://wikimedia.org/api/rest_") reported: "Cannot get mml. Server problem."): {\displaystyle C=x'(s)y''(s)-y'(s)x''(s)\,}

ili u vektorksom obliku

$(\mathbf {r} -\mathbf {r} _{0})\left({\frac {d\mathbf {r} }{ds}}\times {\frac {d^{2}\mathbf {r} }{ds^{2}}}\right)_{0}=0\,$

Glavna okomica

Okomica krivulje koja leži u dodirnoj ravnini se naziva glavna okomica. Njen pravac je isti kao i pravac vektora

Obrada nije uspjela. (Conversion error. Server ("https://wikimedia.org/api/rest_") reported: "Cannot get mml. Server problem."): {\displaystyle \left({\frac {d^{2}\mathbf {r} }{ds^{2}}}\right)_{0}\,}

Dužina ovog vektora se naziva krivina K, a vektoor se naziva zakrivljenim vektorom:

Obrada nije uspjela. (Conversion error. Server ("https://wikimedia.org/api/rest_") reported: "Cannot get mml. Server problem."): {\displaystyle K=\left|{\frac {d^{2}\mathbf {r} }{ds^{2}}}\right|_{0}={\sqrt {\left({\frac {d^{2}x}{ds^{2}}}\right)_{0}^{2}+\left({\frac {d^{2}y}{ds^{2}}}\right)_{0}^{2}+\left({\frac {d^{2}z}{ds^{2}}}\right)_{0}^{2}}}\,}

Površine u R³

Površina u R³ može se napisati u parametarskom obliku

$x=x(u,v)\,$

Obrada nije uspjela. (Conversion error. Server ("https://wikimedia.org/api/rest_") reported: "Cannot get mml. Server problem."): {\displaystyle y=y(u,v)\,}

Obrada nije uspjela. (Conversion error. Server ("https://wikimedia.org/api/rest_") reported: "Cannot get mml. Server problem."): {\displaystyle z=z(u,v)\,}

ili u vektorskom obliku

$\mathbf {r} =\mathbf {r} (u,v)\,$

Jednadžba se može također dati kao

Obrada nije uspjela. (Conversion error. Server ("https://wikimedia.org/api/rest_") reported: "Cannot get mml. Server problem."): {\displaystyle F(x,y,z)=0\,}

ili

Obrada nije uspjela. (Conversion error. Server ("https://wikimedia.org/api/rest_") reported: "Cannot get mml. Server problem."): {\displaystyle z=f(x,y)\,}

U ovom drugom slučaju x i y se mogu smatrati paramtrima, a odakle slijedi jednadžba u parametarskom obliku:

${\begin{aligned}x&=u\\y&=v\\z&=f(u,v)\,\end{aligned}}$

Linijski element

Obrada nije uspjela. (Conversion error. Server ("https://wikimedia.org/api/rest_") reported: "Cannot get mml. Server problem."): {\displaystyle {\begin{aligned}d\mathbf {r} ^{2}&=ds^{2}=dx^{2}+dy^{2}+dz^{2}=\\&=\left[1+\left({\frac {\partial z}{\partial x}}\right)^{2}\right]dx^{2}+2{\frac {\partial z}{\partial x}}{\frac {\partial z}{\partial y}}dx\,dy+\left[1+\left({\frac {\partial z}{\partial y}}\right)^{2}\right]dy^{2}\,\end{aligned}}}

Jednadžba tangente ravnine

Ako je jednadžba površine

Obrada nije uspjela. (Conversion error. Server ("https://wikimedia.org/api/rest_") reported: "Cannot get mml. Server problem."): {\displaystyle F(x,y,z)=0\,}

može se jednadžba tangente ravni napisati u dodirnoj točki (x₀, y₀, z₀):

$(x-x_{0})F_{x_{0}}'+(y-y_{0})F_{y_{0}}'+(z-z_{0})F_{z_{0}}'=0\,$

ili u vektorskom obliku kao

Obrada nije uspjela. (MathML sa SVG ili PNG za rezervu (preporučljivo za moderne preglednike i alate za pristupačnost): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle (\mathbf{r}-\mathbf{r}_0)(\text{grad}\,F)_0=0\,}

Jednadžba okomice na površinu

Ako je jednadžba površine

Obrada nije uspjela. (MathML sa SVG ili PNG za rezervu (preporučljivo za moderne preglednike i alate za pristupačnost): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle F(x,y,z)=0\,}

onda vrijedi za okomicu površine u točki (x₀, y₀, z₀):

Obrada nije uspjela. (MathML sa SVG ili PNG za rezervu (preporučljivo za moderne preglednike i alate za pristupačnost): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{x-x_0}{F_{x_0}'}=\frac{y-y_0}{F_{y_0}'}=\frac{z-z_0}{F_{z_0}'}\,}

ili

Obrada nije uspjela. (MathML sa SVG ili PNG za rezervu (preporučljivo za moderne preglednike i alate za pristupačnost): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mathbf{r}-\mathbf{r}_0=\lambda(\text{grad}\,F)_0\,}