Talesov poučak (prema Talesu iz Mileta) je geometrijski poučak koji kaže da ako su A, B i C točke na kružnici, a dužina između točaka A i C promjer kruga, onda je kut ∠ABC pravi (od 90°).
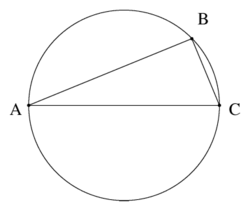
Dokaz
Koristimo sljedeće dokaze: zbroj kutova u trokutu je jednak dvama pravim kutovima (180°) i da su kutovi osnovica jednakokračnih trokuta isti.
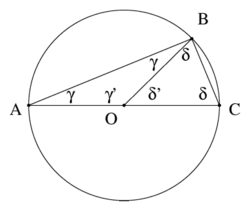
Neka O bude centar trokuta. Pošto je OA = OB = OC, OAB i OBC su jednakokračni trokuti, i po jednakosti kutova jedankokračnih trokuta je OBC = OCB i BAO = ABO. Neka γ = ∠BAO i δ = ∠OBC.
Pošto je zbroj kutova pravokutnog trokuta jednak 180 stupnjeva, imamo:
2γ + γ ′ = 180°
i
2δ + δ ′ = 180°
...također, znamo da je
γ ′ + δ ′ = 180°
Zbrajajući prve dvije jednadžbe i oduzimajući treću, dobivamo
2γ + γ ′ + 2δ + δ ′ − (γ ′ + δ ′) = 180°
...što nakon skraćivanja γ ′i δ ′, dobivamo
γ + δ = 90°