Riemannova zeta-funkcija

Riemannova zeta-funkcija u kompleksnoj ravnini

Riemannova zeta-funkcija za realni s > 1

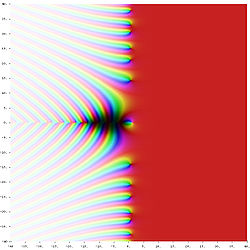
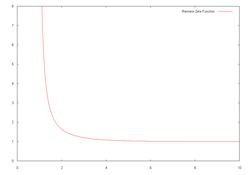
U matematici, Riemannova zeta-funkcija, nazvana po Bernhardu Riemannu, je važna funkcija u teoriji brojeva zbog veze s teoremom o raspodjeli prostih brojeva. Također se primjenjuje u fizici, teoriji vjerojatnosti, i primijenjenoj statistici.

Motivacija

Prvi korak ka Riemannovoj zeta-funkciji bilo je rješenje Baselskog problema, koje je 1735. postigao Leonhard Euler. To je bila suma reda

$\sum _{n=1}^{\infty }{\frac {1}{n^{2}}}=\zeta (2)$.

Koristeći tehnike množenja i faktorizacije konačnih polinoma na beskonačnim polinomima i povlačeći paralelu s Taylorovim redom funkcije sinus, Euler je izveo ζ(2), a ubrzo je svojom tehnikom došao i do izvoda vrijednosti zeta-funkcije i za sve veće parne brojeve. Funkcija je kasnije proširena na sve kompleksne brojeve čiji je realni dio veći od 1.

Riemann je prvi detaljno istražio svojstva funkcije, povezao ju s prostim brojevima te dao tzv. Riemannovu hipotezu, pa se stoga funkcija i naziva po njemu.

Definicija

Funkcija ζ(s) je funkcija kompleksne varijable s i najprije se definirala sljedećom beskonačnom sumom:

$\zeta (s)=\sum _{n=1}^{\infty }{\frac {1}{n^{s}}}$

Leonhard Euler je otkrio vezu zeta-funkcije i raspodjele prostih brojeva:

${\begin{aligned}\sum _{n\geq 1}{\frac {1}{n^{s}}}&=\prod _{p{\text{ prim}}}{\frac {1}{1-p^{-s}}}\\&=\left(1+{\frac {1}{2^{s}}}+{\frac {1}{4^{s}}}+\cdots \right)\left(1+{\frac {1}{3^{s}}}+{\frac {1}{9^{s}}}+\cdots \right)\cdots \left(1+{\frac {1}{p^{s}}}+{\frac {1}{p^{2s}}}+\cdots \right)\cdots ,\end{aligned}}$

gdje, po definiciji, lijeva strana je ζ(s) a beskonačni produkt na desnoj strani je po svim prostim brojevima p.

Zeta-funkcija daje sljedeće vrijednosti za neke odabrane brojeve:

$\zeta (0)=-1/2$

$\zeta (1/2)\approx -1.4603545088095868$

$\zeta (1)=1+{\frac {1}{2}}+{\frac {1}{3}}+\cdots =\infty$; (harmonijski red)

$\zeta (3/2)\approx 2.612$; koristi se za računanje kritične temperature Bose–Einsteinovog kondenzata u fizici.

$\zeta (2)=1+{\frac {1}{2^{2}}}+{\frac {1}{3^{2}}}+\cdots ={\frac {\pi ^{2}}{6}}\approx 1.645$; dokaz ove jednakosti je tzv. Bazelski problem.

$\zeta (5/2)\approx 1.341$

$\zeta (3)=1+{\frac {1}{2^{3}}}+{\frac {1}{3^{3}}}+\cdots \approx 1.202$; tzv. Apéryjeva konstanta

$\zeta (7/2)\approx 1.127$

$\zeta (4)=1+{\frac {1}{2^{4}}}+{\frac {1}{3^{4}}}+\cdots ={\frac {\pi ^{4}}{90}}\approx 1.0823$

Poznato je da zeta-funkcija ima nultočke -2, -4, -6... One se nazivaju trivijalnima. Hipoteza da sve ostale (kompleksne) nultočke imaju realni dio jednak 1/2 je poznata kao Riemannova hipoteza i do sada nije riješena.

Vidi još

• prosti brojevi
• Leonhard Euler
• Bernhard Riemann

Izvori

Literatura

• Bernhard Riemann, Über die Anzahl der Primzahlen unter einer gegebenen Grösse (1859). In Gesammelte Werke, Teubner, Leipzig (1892), Reprinted by Dover, New York (1953).
• Jacques Hadamard, Sur la distribution des zéros de la fonction ζ(s) et ses conséquences arithmétiques, Bulletin de la Societé Mathématique de France 14 (1896) pp 199-220.
• Helmut Hasse, Ein Summierungsverfahren für die Riemannsche ζ-Reihe, (1930) Math. Z. 32 pp 458-464. (Globally convergent series expression.)
• E. T. Whittaker and G. N. Watson (1927). A Course in Modern Analysis, fourth edition, Cambridge University Press (Chapter XIII).

Vanjske poveznice

• Riemann Zeta Function, in Wolfram Mathworld - objašnjenje koje koristi matematički pristup (eng.)
• Tablica odabranih nultočki

1. PREUSMJERI Predložak:Kategorizirati