Polinom

Polinom je matematička funkcija s jednom ili više varijabla koja se može zapisati kao linearna kombinacija umnožaka njihovih potencija, odnosno kao zbroj monoma sastavljenih od umnožaka konstante i kombinacija potencija svake od varijabla. Polinom n-tog stupnja u jednoj varijabli je funkcija

$P(x)=a_{n}x^{n}+a_{n-1}x^{n-1}+...+a_{1}x+a_{0}$

u kojoj su koeficijenti je Obrada nije uspjela. (MathML sa SVG ili PNG za rezervu (preporučljivo za moderne preglednike i alate za pristupačnost): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle a_{0}} , Obrada nije uspjela. (MathML sa SVG ili PNG za rezervu (preporučljivo za moderne preglednike i alate za pristupačnost): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle a_{1}} ,..., Obrada nije uspjela. (MathML sa SVG ili PNG za rezervu (preporučljivo za moderne preglednike i alate za pristupačnost): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle a_{n}} konstante i $a_{n}\neq 0$. Broj Obrada nije uspjela. (MathML sa SVG ili PNG za rezervu (preporučljivo za moderne preglednike i alate za pristupačnost): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle a_{0}} zove se slobodni koeficijent, a broj Obrada nije uspjela. (MathML sa SVG ili PNG za rezervu (preporučljivo za moderne preglednike i alate za pristupačnost): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle a_{n}} vodeći koeficijent.

Polinomi se skraćeno zapisuju pomoću simbola za zbrajanje,

Obrada nije uspjela. (MathML sa SVG ili PNG za rezervu (preporučljivo za moderne preglednike i alate za pristupačnost): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle P(x)=\sum _{i=0}^{n}a_{i}x^{i}} .

Ponekad se polinomom zove sam polinomni izraz sa zbrojem raznih potencija neke veličine ili izraza, pa se pripadna funkcija navodi kao polinomna funkcija.

Stupanj polinoma Obrada nije uspjela. (MathML sa SVG ili PNG za rezervu (preporučljivo za moderne preglednike i alate za pristupačnost): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle P(x)=a_{n}x^{n}+a_{n-1}x^{n-1}+...+a_{0}} za $a_{n}\neq 0$ je broj Obrada nije uspjela. (MathML sa SVG ili PNG za rezervu (preporučljivo za moderne preglednike i alate za pristupačnost): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle n} . Pišemo Obrada nije uspjela. (MathML sa SVG ili PNG za rezervu (preporučljivo za moderne preglednike i alate za pristupačnost): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle {\text{deg}}P=n} .

Polinomi imaju ključnu ulogu u proučavanju algebarskih brojeva te su česti u drugim granama znanosti poput fizike i računarstva.

Monomi, binomi, trinomi, itd.

Pribrojnici u polinomu nazivaju se monomi; oni su i sami polinomi s jednim članom. Monom je umnožak konstante i bilo koje kombinacije potencija varijabla. Tako su, na primjer

Obrada nije uspjela. (MathML sa SVG ili PNG za rezervu (preporučljivo za moderne preglednike i alate za pristupačnost): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle -7x^{2}} ,  Obrada nije uspjela. (MathML sa SVG ili PNG za rezervu (preporučljivo za moderne preglednike i alate za pristupačnost): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle 3x^{2}y} ,  $-{\tfrac {1}{4}}xy^{5}z^{2}$,  Obrada nije uspjela. (MathML sa SVG ili PNG za rezervu (preporučljivo za moderne preglednike i alate za pristupačnost): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \xi y^{4}}

monomi u varijablama Obrada nije uspjela. (MathML sa SVG ili PNG za rezervu (preporučljivo za moderne preglednike i alate za pristupačnost): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle x} , Obrada nije uspjela. (MathML sa SVG ili PNG za rezervu (preporučljivo za moderne preglednike i alate za pristupačnost): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle y} i Obrada nije uspjela. (MathML sa SVG ili PNG za rezervu (preporučljivo za moderne preglednike i alate za pristupačnost): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle z} .

Polinom koji u temeljnom obliku ima samo dva člana naziva se binom. Polinom s tri člana je trinom. Tako je npr. kvadrat binoma jednak trinomu u dvije varijable:

Obrada nije uspjela. (MathML sa SVG ili PNG za rezervu (preporučljivo za moderne preglednike i alate za pristupačnost): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle P(x,y)=(\underbrace {x-y} _{\text{binom}})^{2}=\underbrace {x^{2}-2xy+y^{2}} _{\text{trinom}}}

Obrada nije uspjela. (MathML sa SVG ili PNG za rezervu (preporučljivo za moderne preglednike i alate za pristupačnost): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle P(x,y)=(\underbrace {x^{2}+y} _{\text{binom}})^{2}=\underbrace {x^{4}+2x^{2}y+y^{2}} _{\text{trinom}}}

Nul-polinom

Ako je polinom jednak nuli za sve vrijednosti svojih varijabli nazivamo ga nul-polinom i za nj ne definiramo stupanj (ili se ponegdje formalno uzima da je njegov stupanj $-\infty$ ili Obrada nije uspjela. (MathML sa SVG ili PNG za rezervu (preporučljivo za moderne preglednike i alate za pristupačnost): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle -1} , ovisno o autoru).

Računske operacije s polinomima

Dva polinoma možemo zbrajati, oduzimati, množiti i dijeliti. Zbrajanje i množenje je komutativno te vrijede uobičajena algebarska pravila. Rezultat dijeljenja dva polinoma nije uvijek polinom: očigledan primjer je dijeljenje polinoma Obrada nije uspjela. (MathML sa SVG ili PNG za rezervu (preporučljivo za moderne preglednike i alate za pristupačnost): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle n} -tog stupnja polinomom Obrada nije uspjela. (MathML sa SVG ili PNG za rezervu (preporučljivo za moderne preglednike i alate za pristupačnost): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle m} -tog stupnja kada je Obrada nije uspjela. (MathML sa SVG ili PNG za rezervu (preporučljivo za moderne preglednike i alate za pristupačnost): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle n<m} .

Uočimo da oduzeti dva polinoma možemo tako da polinom koji je u funkciji umanjitelja pomnožimo s Obrada nije uspjela. (MathML sa SVG ili PNG za rezervu (preporučljivo za moderne preglednike i alate za pristupačnost): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle (-1)} te ga zbrojimo s polinomom umanjenikom.

Primjeri

Uzmimo Obrada nije uspjela. (MathML sa SVG ili PNG za rezervu (preporučljivo za moderne preglednike i alate za pristupačnost): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle P(x)=x^{2}+x-2} i $Q(x)=x-1$.

Njihovi zbroj i umnožak su:

Obrada nije uspjela. (MathML sa SVG ili PNG za rezervu (preporučljivo za moderne preglednike i alate za pristupačnost): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle P(x)+Q(x)=x^{2}+2x-3} ,

Obrada nije uspjela. (MathML sa SVG ili PNG za rezervu (preporučljivo za moderne preglednike i alate za pristupačnost): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle P(x)\cdot Q(x)=x^{3}-3x+2} .

Opišimo kako algoritamski podijeliti ova dva polinoma. Ovdje je, radi jednostavnosti, rezultat dijeljenja polinom. Želimo izračunati Obrada nije uspjela. (MathML sa SVG ili PNG za rezervu (preporučljivo za moderne preglednike i alate za pristupačnost): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle {\frac {P(x)}{Q(x)}}=R(x).}

Ta jednadžba ekvivalentna je s Obrada nije uspjela. (MathML sa SVG ili PNG za rezervu (preporučljivo za moderne preglednike i alate za pristupačnost): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle x^{2}+x-2=(x-1)R(x).} Prvi član polinoma $R(x)$ jednak je Obrada nije uspjela. (MathML sa SVG ili PNG za rezervu (preporučljivo za moderne preglednike i alate za pristupačnost): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle x} jer množenjem s Obrada nije uspjela. (MathML sa SVG ili PNG za rezervu (preporučljivo za moderne preglednike i alate za pristupačnost): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle (x-1)} mora dati član s jediničnim koeficijentom najveće potencije 2: Obrada nije uspjela. (MathML sa SVG ili PNG za rezervu (preporučljivo za moderne preglednike i alate za pristupačnost): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle (x^{2}+x-2)=(x-1)({\color {Red}x}+\dots )}

Ostatak (...) je neki polinom Obrada nije uspjela. (MathML sa SVG ili PNG za rezervu (preporučljivo za moderne preglednike i alate za pristupačnost): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle T(x)} pa u prvom koraku imamo

Obrada nije uspjela. (MathML sa SVG ili PNG za rezervu (preporučljivo za moderne preglednike i alate za pristupačnost): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle (x^{2}+x-2)=(x-1)({\color {Red}x}+T(x))}

$(x^{2}+x-2)=x^{2}-x+(x-1)T(x)$.

Dobivamo Obrada nije uspjela. (MathML sa SVG ili PNG za rezervu (preporučljivo za moderne preglednike i alate za pristupačnost): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle 2x-2=(x-1)T(x)} čime je problem dijeljenja sveden na dijeljenje polinoma stupnja nižeg za 1.

U drugom koraku rješavamo Obrada nije uspjela. (MathML sa SVG ili PNG za rezervu (preporučljivo za moderne preglednike i alate za pristupačnost): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle 2x-2=(x-1)T(x)} .

Obrada nije uspjela. (MathML sa SVG ili PNG za rezervu (preporučljivo za moderne preglednike i alate za pristupačnost): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle T(x)} može jedino biti polinom stupnja 0 jer množeći Obrada nije uspjela. (MathML sa SVG ili PNG za rezervu (preporučljivo za moderne preglednike i alate za pristupačnost): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle (x-1)} ne smije dati potencije veće od 1: Obrada nije uspjela. (MathML sa SVG ili PNG za rezervu (preporučljivo za moderne preglednike i alate za pristupačnost): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle 2x-2=(x-1)({\color {Red}2}+\dots )} .

Ostatak (...) može biti samo nulpolinom, tj. 0. Mogli smo uočiti da je Obrada nije uspjela. (MathML sa SVG ili PNG za rezervu (preporučljivo za moderne preglednike i alate za pristupačnost): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle 2x-2=(x-1)\cdot 2} .

Rješenje je $R(x)=({\color {Red}x}+{\color {Red}2}+{\color {Red}0})$, odnosno Obrada nije uspjela. (MathML sa SVG ili PNG za rezervu (preporučljivo za moderne preglednike i alate za pristupačnost): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle R(x)=x+2} .

Uporaba polinoma

Zbog jednostavnosti računanja s polinomima, posebno njihovog strojnog izvrjednjavanja, vrijedosti mnogih drugih funkcija često se aproksimiraju polinomom određenog stupnja na određenom intervalu. Ako je vrijednost funkcije poznata u konačno mnogo točaka, vrijednosti između točaka mogu se procijeniti interpolacijom iz polinoma koji u tim točkama daje egzaktne vrijednosti ili regresijom uz pomoć polinoma po volji izabranog stupnja koji po svim poznatim točkama daje najmanju pogrešku.

• 
  Vrijednosti nepoznate funkcije poznate su u sedam točaka
• 
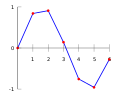
  Vrijednosti između točaka mogu se procijeniti linearnom interpolacijom od točke do točke
• 
  Vrijednosti između točaka procijenjene interpolacijskim polinomom šestoga stupnja

Nultočke polinoma

U primjeni, kao i u teoriji, često je potrebno znati u kojim točkama polinomi poprimaju vrijednost nula. Te se točke nazivaju nultočkama ili korijenima polinoma. Ako je Obrada nije uspjela. (MathML sa SVG ili PNG za rezervu (preporučljivo za moderne preglednike i alate za pristupačnost): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \alpha } nultočka polinoma Obrada nije uspjela. (MathML sa SVG ili PNG za rezervu (preporučljivo za moderne preglednike i alate za pristupačnost): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle P(x)} , vrijedi $P(\alpha )=0$. Prema Bézoutovom poučku za polinome, $(x-\alpha )$ tada dijeli $P(x)$. Iz ovog poučka i osnovnog teorema algebre, koji kaže da svaki polinom stupnja većeg od nule ima nultočku u skupu kompleksnih brojeva, slijedi da svaki polinom n-tog stupnja u jednoj varijabli ima točno n nultočaka u skupu kompleksnih brojeva, s tim da pritom neke nultočke mogu biti višestruke kratnosti, odnosno da za neke nultočke može i $(x-\alpha )^{k}$ dijeliti $P(x)$, gdje se najveći takav $k$ naziva kratnošću nultočke. Vrijedi i sljedeće: ako su $\alpha _{1}$,$\alpha _{2}$, ..., $\alpha _{n}$ kompleksne nultočke polinoma $P(x)$ s vodećim koeficijentom $a_{n}$, on se može na jedinstven način zapisati kao umnožak n polinoma prvoga stupnja,

Obrada nije uspjela. (MathML sa SVG ili PNG za rezervu (preporučljivo za moderne preglednike i alate za pristupačnost): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle P(x)=a_{n}(x-\alpha _{1})(x-\alpha _{2})\dots (x-\alpha _{n})}