Hookeov zakon
1. Vlačna čvrstoća materijala
2. Granica razvlačenja ili σ0,2
3. Lom materijala
4. Područje plastičnih deformacija
5. Područje klonulosti
A: Teoretski dijagram rastezanja
B: Stvarni dijagram rastezanja (F/A)

Hookeov zakon je zakonitost koja opisuje ovisnost promjene oblika čvrstoga tijela u obliku štapa o djelovanju vanjske sile, što ju je utvrdio Robert Hooke. Opterećenjem izazvano naprezanje σ razmjerno je deformaciji ε, odnosno:
Faktor razmjernosti E je modul elastičnosti i karakterističan je za pojedini materijal. Do određene granice naprezanja Hookeov zakon može se primijeniti na većinu konstrukcijskih materijala. Za složenija opterećenja tijela različitih oblika rabi se Hookeov zakon u poopćenom obliku, koji se izražava s više skalarnih linearnih jednadžba.[1]
Primjena Hookeovog zakona
Ako je šipka ili štap od nekog elastičnog materijala, onda i nju možemo promatrati kao oprugu. Šipka ima duljinu L i poprečni presjek A. Ako šipku razvlačimo s nekom silom F, onda u njoj nastaje naprezanje σ, koje se opire vanjskoj sili. Tada Hookeov zakon možemo pisati u drugom obliku:[2]
ili
gdje je: σ – naprezanje u šipki ili štapu (N/mm2), E – Youngov modul elastičnosti (N/mm2), ε – omjer produljenja šipke ili štapa i njene duljine (bez dimenzije ili ΔL / L), L – duljina štapa, ΔL - produljenje šipke ili štapa (mm), F – sila koja produljuje šipku ili štap (N), A – poprečni presjek šipke ili štapa (mm2) [3]
Hookeov zakon vrijedi samo u određenom području nekog materijala, koje se naziva elastično područje. Za čelik je elastično područje sve do granice razvlačenja ili gdje ta granica nije jasno određena, do granice plastičnosti koja je određena onim naprezanjem pri kojem nastaje trajno produljenje od 0,2% prvobitne dužine šipke ili štapa. Ovo naprezanje nosi oznaku σ0,2.[4]
Opruge
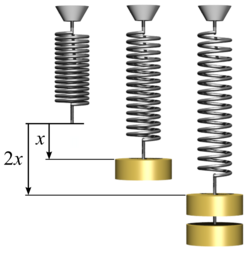
Ako se tijelo na elastičnoj opruzi pomakne iz ravnotežnog položaja, tj. ako se opruga rastegne ili stisne, djelovat će povratna sila (elastična sila opruge), koja će nastojati tijelo vratiti u ravnotežni položaj. Iznos te sile je proporcionalan pomaku tijela iz ravnotežnog položaja. Dakle, ako je pomak x, povratna sila je:
a koeficijent proporcionalnosti k je konstanta opruge (ovisi o njenim dimenzijama, obliku i materijalu od kojega je izrađena)
Dijagram naprezanja
Dijagram naprezanja prikazuje medusobnu ovisnost σ - vlačnog naprezanja i ε - relativnog produljenja ili linijske vlačne deformacije. U materijalu koji je opterećen nekom silom F nastaju naprezanja σ koja uzrokuju njegovo rastezanje. Naprezanje σ je omjer sile F i ploštine A presjeka štapa ili šipke (okomitog na smjer sile).
Zbog djelovanja sile F (a time nastalog naprezanja σ) štap ili šipka će se od početne duljine L0 rastegnuti na duljinu L. Tako je produljenje štapa ili šipke:
Relativno produljenje ε (duljinska ili uzdužna deformacija) štapa ili šipke je produljenje s obzirom na početnu duljinu Lo. Početno je naprezanje linearno (deformacija je izravno razmjerna naprezanju). U području linearnog rastezanja (Hookeov zakon) materijal je elastičan i nakon prestanka djelovanja sile, odnosno naprezanja, on se vraća u početno stanje. Youngov modul elastičnosti je omjer naprezanja i relativnog produljenja (u području elastičnosti).
Tehnička granica elastičnosti je naprezanje pri kojem osjetljiva mjerila osjete prvo primjetno trajno produljenje materijala (pri još nepromijenjenom presjeku Ao). Nakon te granice (obično na kraju linearnog rastezanja) materijal se rasteže plastično i nakon prestanka djelovanja sile ne vraća se više na početnu duljinu L0, već ostaje određeno trajno produljenje, uz suženje presjeka, A < A0.
Izvori
- ↑ Hookeov zakon, [1] (Arhivirano 21. siječnja 2019.) "Hrvatska enciklopedija", Leksikografski zavod Miroslav Krleža, www.enciklopedija.hr, 2015.
- ↑ [2] (Arhivirano 28. veljače 2017.) "Konstrukcijski elementi I", Tehnički fakultet Rijeka, Božidar Križan i Saša Zelenika, 2011.
- ↑ [3] (Arhivirano 31. siječnja 2012.) "Elementi strojeva", Fakultet elektrotehnike, strojarstva i brodogradnje Split, Prof. dr. sc. Damir Jelaska, 2011.
- ↑ "Elementi strojeva", Karl-Heinz Decker, Tehnička knjiga Zagreb, 1975.




