Potencija točke
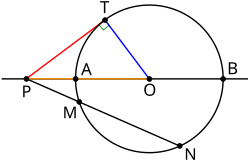
U geometriji, potencija točke govori o udaljenosti neke točke od neke kružnice. Neka je točka P, a kružnica k sa središtem u S i polumjerom r. Tada je potencija točke P s obzirom na kružnicu k jednaka |PS|2 - r2 (Slika 1). Ako je ona manja od nule, točka je unutar kružnice; ako je jednaka nuli, točke je na kružnici; te ako je veća od nule, točka se nalazi izvan kružnice. Ako je proizvoljna točka A na kružnici, pravac PA siječe kružnicu u točkama A i B, tada je potencija točke jednaka |PA| · |PB|. Neka je p tangenta na kružnicu k koja prolazi kroz P, te je T diralište tangente p. Tada je potencija točke jednaka |PT|2.
Radikalna os ili potencijalna os je skup točaka ravnine koje imaju jednaku potenciju na dvije nekoncentrične kružnice. Radikalna os je pravac okomit na spojnicu središta tih kružnica. Ako se kružnice sijeku, radikalna os prolazi kroz sjecišta kružnica.
Radikalno središte je točka koja ima jednaku potenciju na tri nekoncentrične kružnice. Ako se tri kružnice sijeku u jednoj točci, upravo je ta točka njihovo radikalno središte. Vukorepin teorem kaže kako se rješava svaki problem koji sadržava tri pravca koja prolaze kroz šest različitih točaka (svaki pravac kroz dvije) i sijeku se u jednoj točci s radikalnim središtem. Radikalno središte se uvijek dokazuje uvođenjem fantomske točke koja je sjecište dviju kružnica i dokazivanjem da ona leži na trećoj.
Dokaz
Potencija točke dokazuje se sličnim trokutima. Neka su |PA| · |PB| te |PM| · |PN| potencije točke s obzirom na kružnicu k. Trokuti PAM i PBN su slični (ali ne homotetični). Iz sličnosti slijedi:
što je i trebalo dokazati.
Dokaz za tangentne dužine koje spajaju diralište tangente i točku, uz oznake kao na slici 1:
gdje su točke P, A i B kolinearne.
Vidi još
![]() Nedovršeni članak Potencija točke koji govori o geometriji treba dopuniti. Dopunite ga prema pravilima uređivanja Hrvatske internetske enciklopedije.
Nedovršeni članak Potencija točke koji govori o geometriji treba dopuniti. Dopunite ga prema pravilima uređivanja Hrvatske internetske enciklopedije.


