Fibonaccijev broj

Fibonaccijevi brojevi oblikuju niz definiran sljedećom rekurzivnom relacijom:

[math]\displaystyle{ F(n):= \begin{cases} 0 & \mbox{ako je } n = 0; \\ 1 & \mbox{ako je } n = 1; \\ F_{n-1} + F_{n-2}\!\, & \mbox{ako je } n \gt 1. \\ \end{cases} }[/math]

Dakle, nakon dvije početne vrijedosti, svaki sljedeći broj je zbroj dvaju prethodnika. Primjerice, [math]\displaystyle{ 2 + 3 }[/math] dat će [math]\displaystyle{ 5 }[/math], [math]\displaystyle{ 3 + 5 }[/math] dat će [math]\displaystyle{ 8 }[/math], itd.

Prvi Fibonaccijevi brojevi, također označeni kao [math]\displaystyle{ F_n }[/math], za [math]\displaystyle{ n = 0, 1, 2, ... }[/math] su redom [math]\displaystyle{ 1, 1, 2, 3, 5, 8, 13, 21, ... }[/math]

Treba napomenuti da Fibonaccijev niz ipak može početi i s [math]\displaystyle{ F_1 = 1 }[/math] umjesto s [math]\displaystyle{ F_0 = 0, }[/math] no to često nije bitno u konkretnim razmatranjima svojstava tog niza.

Popločanje s kvadratima čije su stranice po duljini sukcesivni Fibonaccijevi brojevi

Fibonaccijeva spirala, stvorena iscrtavanjem lukova koji spajaju suprotne kuteve kvadrata u Fibonaccijevom popločanju prikazanom gore – vidjeti zlatna spirala.

Fibonaccijevi brojevi su imenovani po Leonardu od Pise, poznatom kao Fibonacci, iako su ranije opisani u Indiji.

Osnovna svojstva

Svojstva vezana uz djeljivost

• Svaka dva uzastopna Fibonaccijeva broja su relativno prosta. Dokažimo to. Pretpostavimo da je [math]\displaystyle{ M(F_{n - 1}, F_n) = d. }[/math] No, onda je [math]\displaystyle{ d | F_{n} - F_{n - 1} = F_{n - 2}. }[/math] Analogno, [math]\displaystyle{ d | F_{n - 3}, F_{n - 4}, ..., F_1 = 1 }[/math] što povlači [math]\displaystyle{ d = 1. }[/math]

• Vrijedi

[math]\displaystyle{ F_n | F_{kn}, \forall k \in \mathbb{N} }[/math].

Ovo se svojstvo lako pokaže indukcijom. Za [math]\displaystyle{ k = 1 }[/math], tvrdnja je očita. Pretpostavimo da tvrdnja vrijedi za neki [math]\displaystyle{ k }[/math]. Uočimo sada da je [math]\displaystyle{ F_{k + 1}n = F_{kn + n} }[/math], tj. [math]\displaystyle{ F_{(k + 1)n} = F_{kn - 1}F_{n} + F_{kn}F_{n + 1} }[/math] (vidjeti vezu s Morseovim kodom). Kako [math]\displaystyle{ F_n | F_{kn} }[/math] iz gornje jednakosti slijedi [math]\displaystyle{ F_n | F_{(k + 1)n} }[/math], čime je tvrdnja dokazana.

• Vrijedi:

[math]\displaystyle{ M(F_m, F_n) = F_{M(m, n)} }[/math].

Neka je [math]\displaystyle{ M(m, n) = d }[/math]. Kako, prema gornjoj jednakosti [math]\displaystyle{ F_d | F_m, F_n }[/math]. (Jer su [math]\displaystyle{ m, n }[/math] višekratnici od [math]\displaystyle{ d }[/math].) Iz ovoga očito slijedi [math]\displaystyle{ F_d | M(F_m, F_n) }[/math]. (1)

Prema Bézoutovoj lemi se [math]\displaystyle{ d }[/math] može prikazati kao linearna kombinacija [math]\displaystyle{ am + bn }[/math] za cijele brojeve [math]\displaystyle{ a, b }[/math].

Zato je [math]\displaystyle{ F_d = F_{am + bn} }[/math] pa slijedi da se [math]\displaystyle{ F_d }[/math] može zapisati kao linearna kombinacija [math]\displaystyle{ F_m, F_n }[/math] jer je [math]\displaystyle{ F_d = F_{am - 1}F_{bn} + F_{am}F_{bn + 1} }[/math]. Dakle, [math]\displaystyle{ M(F_m, F_n) | F_d }[/math]. (2)

Iz (1) i (2) slijedi [math]\displaystyle{ F_d = M(F_m, F_n) }[/math], što je i trebalo pokazati.

Druga važna svojstva

• Vrijedi [math]\displaystyle{ F_n = \frac{1}{\sqrt{5}}[{(\frac{1 + \sqrt{5}}{2})}^n - {(\frac{1 - \sqrt{5}}{2})}^n]. }[/math] Ovo se važno svojstvo Fibonaccijevih brojeva naziva Binetova formula.

• Vrijedi [math]\displaystyle{ F_{n - 1}F_{n + 1} = F_n^2 + (- 1)^n, n \geq 2.. }[/math] Ovo se pravilo naziva Cassinijev identitet.

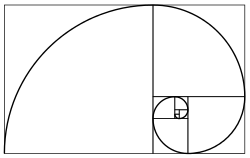
Povezanost sa zlatnim rezom

Ako imamo dvije dužine, jednu dužu i jednu kraću te ako je omjer duljina duže na prema kraćoj dužini jednak zlatnom rezu ([math]\displaystyle{ \approx 1.618 }[/math]), tada je zlatnom rezu jednak i omjer zbroja duljina duže i kraće dužine na prema duljini duže.

Vidjet ćemo da se slična relacija može naći u omjerima triju uzastopnih Fibonaccijevih broja, [math]\displaystyle{ F_{n - 1}, F_n, F_{n + 1}. }[/math] Naime, iz Cassinijevog identiteta dijeljenjem obje strane s [math]\displaystyle{ F_{n - 1}F_n, }[/math] slijedi [math]\displaystyle{ \frac{F_n}{F_{n - 1}} = \frac{F_{n + 1}}{F_n} + \frac{(- 1)^n}{F_{n - 1}F_n}. }[/math]

Kada [math]\displaystyle{ n \rightarrow \infty }[/math] možemo zanemariti drugi pribrojnik pa dobivamo [math]\displaystyle{ \frac{F_n}{F_{n - 1}} = \frac{F_{n + 1}}{F_n} }[/math] što zadovoljava povijesnu (geometrijsku) definiciju zlatnog reza navedenu gore.

Veza s Morseovim kodom

Morseov kod je niz točaka i crtica. Duljinu Morseovog koda definiramo tako da svaka točka pridonosi duljinu 1, a svaka crtica duljinu 2.

Prema tome, ako imamo Morseov kod duljine n, onda možemo zamisliti da imamo n pozicija od kojih su neke spojene crticama, a na ostalima se nalaze točke.

Zato možemo zamisliti da je crtica zapravo spojnica dviju točaka, ali dvije crtice ne mogu stajati jedna pored druge (razmak mora biti najmanje jedna ili više točaka).

Označimo sada s [math]\displaystyle{ M_n }[/math] broj svih Morseovih kodova duljine [math]\displaystyle{ n }[/math]. Dokazat ćemo relaciju [math]\displaystyle{ M_n = M_{n - 1} + M_{n - 2} }[/math] koja je posve ekvivalentna rekurzivnoj formuli Fibonaccijeva niza.

Naime, Morseov kod duljine [math]\displaystyle{ n }[/math] može započeti točkom (takvih ima [math]\displaystyle{ M_{n - 1} }[/math]) ili crticom (takvih ima [math]\displaystyle{ M_{n - 2} }[/math]). Dakle, očito je [math]\displaystyle{ M_n = M_{n - 1} + M_{n - 2} }[/math] te vrijedi [math]\displaystyle{ M_1 = 1 }[/math], [math]\displaystyle{ M_2 = 2 }[/math] iz čega slijedi direktna veza s Fibonaccijevim nizom: [math]\displaystyle{ M_n = F_{n + 1} }[/math].

Važni identiteti

Vrijedi:

[math]\displaystyle{ F_{m + n} = F_{m - 1}F_n + F_mF_{n + 1} }[/math]

Dokaz. Gore smo pokazali da je [math]\displaystyle{ F_{m + n} }[/math] jednak broju [math]\displaystyle{ M_{m + n - 1} }[/math] svih Morseovih kodova duljine [math]\displaystyle{ m + n - 1 }[/math].

Uočimo sada u svakom takvom kodu [math]\displaystyle{ (m - 1) }[/math]-vu i [math]\displaystyle{ m }[/math]-tu poziciju. Morseove kodove ćemo podijeliti na one koji imaju crticu između te dvije pozicije i na one koji ju nemaju.

Jasno je da kod koji ima crticu između [math]\displaystyle{ (m - 1) }[/math]-ve i [math]\displaystyle{ m }[/math]-te pozicije može na prve [math]\displaystyle{ m - 2 }[/math] pozicije imati bilo kakav Morseov kod, a potom mora imati crticu, a zatim na zadnjih [math]\displaystyle{ (m + n - 1) - m = n - 1 }[/math] pozicija može ponovno imati bilo kakav Morseov kod pa takvih kodova očigledno ima [math]\displaystyle{ M_{n - 2}M_{n - 1} = F_{m - 1}F_n }[/math]. S druge strane, kod koji nema crticu između [math]\displaystyle{ (m - 1) }[/math]-ve i [math]\displaystyle{ m }[/math]-te pozicije može na prvih [math]\displaystyle{ m - 1 }[/math] pozicija imati bilo kakav Morseov kod, kao i na zadnjih [math]\displaystyle{ (m + n - 1) - (m - 1) = n }[/math] pozicija. Zato takvih kodova ima [math]\displaystyle{ M_{m - 1}M_n = F_mF_{n + 1} }[/math], čime je identitet dokazan.

Od ostalih identiteta s Fibonaccijevim brojevima koji su vezani uz Morseov kod, po važnosti se ističu sljedeći:

• [math]\displaystyle{ F_{2n} = F^2_{n + 1} - F^2_{n - 1} }[/math],
• [math]\displaystyle{ F_{2n + 1} = F^2_n + F^2_{n + 1} }[/math],
• [math]\displaystyle{ F_1 + F_2 + ... + F_n = F_{n + 2} - 1 }[/math].

Varijacije Fibonaccijevog niza

Možemo konstruirati nove nizove za koje neće nužno vrijediti [math]\displaystyle{ F_1 = F_2 = 1 }[/math] kao što to vrijedi za Fibobaccijev niz. No, željet ćemo da osnovno pravilo, odnosno identitet, [math]\displaystyle{ F_n = F_{n - 2} + F_{n - 1} }[/math] vrijedi za sve te nizove. Takve nizove jednim imenom nazivamo generalizirani Fibonaccijevi nizovi.

Uočimo da je neki takav niz [math]\displaystyle{ a_{(F_1, F_2)} }[/math] zadan ako su zadani [math]\displaystyle{ F_1, F_2 \in \mathbb{N}. }[/math]

No, dakako da [math]\displaystyle{ F_1, F_2 }[/math] mogu biti negativni. Uočimo da će [math]\displaystyle{ F_n \rightarrow -\infty }[/math] kada [math]\displaystyle{ n \rightarrow \infty }[/math] samo ako je [math]\displaystyle{ F_1, F_2 \lt 0 }[/math] ili bez smanjenja općenitosti (možemo permutirati [math]\displaystyle{ F_1, F_2 }[/math]) kada je [math]\displaystyle{ |F_1| \gt |F_2|, F_1 \lt 0, F_2 \gt 0. }[/math]

Primjeri

Ovdje su primjeri takvih nizova: [math]\displaystyle{ a_{(5,5)} = 5, 5, 10, 15, 35, ... }[/math], [math]\displaystyle{ a_{(3, 8)} = 3, 8, 11, 19, ... }[/math], no možemo formirati niz za koji vrijedi [math]\displaystyle{ F_1 \gt F_2 }[/math] kao npr. [math]\displaystyle{ a_{(4, 2)} = 4, 2, 6, 8, ... }[/math]

Lucasovi brojevi

Za [math]\displaystyle{ F_1 = 2, F_2 = 1 }[/math] dobivamo niz tzv. Lucasovih brojeva nazvanih po francuskom matematičaru Françoisu Édouardu Anatoleu Lucasu (1842. - 1891.).

Evo prvih nekoliko članova tog niza: [math]\displaystyle{ 2, 1, 3, 4, 7, 11, ... }[/math]

Trojke generaliziranog Fibonaccijevog niza

Tri utastopna člana [math]\displaystyle{ F_{n}, F_{n + 1}, F_{n + 2} }[/math] Fibonaccijevog niza zajednički zovemo trojka generaliziranog Fibobaccijevog niza. Uočimo da za [math]\displaystyle{ n \in \{2, 3, ...\} }[/math] vrijedi [math]\displaystyle{ F_{n} \lt F_{n + 1} \lt F_{n + 2}. }[/math] (Za [math]\displaystyle{ n = 1 }[/math] sustav nejednakosti [math]\displaystyle{ F_n \lt F_{n + 1} \lt F_{n + 2} }[/math] ipak ne vrijedi ako niz počinje s [math]\displaystyle{ F_2 \leq F_1. }[/math])

Dakle, intuitivno je da vrijedi [math]\displaystyle{ F_nF_{n + 2} \approx F_{n + 1}F_{n + 1}. }[/math] Zapravo, ispravno je [math]\displaystyle{ F_nF_{n + 2} = F_{n + 1}F_{n + 1} + (- 1)^{n + 1} }[/math] prema Cassinijevom identitetu. Označimo sada s [math]\displaystyle{ D = F_nF_{n + 2} - F_{n + 1}F_{n + 1}. }[/math]

Pretpostavimo sada da su [math]\displaystyle{ F_1 \leq F_2 }[/math] dva početna broja niza za kojeg vrijedi osnovna relacija iz Fibonaccijevog niza.

Hoće li umnožak prvog i trećeg člana, [math]\displaystyle{ F_n \cdot F_{n + 2} }[/math], neke trojke biti veći za 1 odnosno manji za 1 od kvadrata srednjeg člana, [math]\displaystyle{ F_{n + 1} }[/math], te trojke isključivo ovisi o razlici [math]\displaystyle{ d }[/math] prvog i drugog člana tog niza, [math]\displaystyle{ d = F_2 - F_1 }[/math].

Ispišimo prvih nekoliko članova tog niza: [math]\displaystyle{ F_1 = x, F_2 = x + d, F_3 = 2x + d, F_4 = 3x + 2d, ... }[/math]

Slučaj 1., [math]\displaystyle{ F_1 = F_2 }[/math]

Ovdje će vrijediti [math]\displaystyle{ F_nF_{n + 2} = F_{n + 1}F_{n + 1} + (- 1)^nF^2, }[/math] tj. vrijedit će [math]\displaystyle{ D = F^2 }[/math] ako je [math]\displaystyle{ n }[/math] paran, odnosno [math]\displaystyle{ D = - d^2 }[/math] ako je neparan. (1)

Dokaz. Uočimo da je [math]\displaystyle{ d = 0. }[/math] Ispišimo nekoliko članova ovog niza: [math]\displaystyle{ x, x, x + x, (x + x) + x, ... = x, x, 2x, 3x, ... }[/math] Za prvu trojku [math]\displaystyle{ T_1 = (x, x, x + x) }[/math] vrijedi (1) jer je [math]\displaystyle{ D = (x + x)x - xx = xx = x^2 = F^2. }[/math] Za sljedeću trojku [math]\displaystyle{ T_2 = (x, 2x, 3x) }[/math] računamo [math]\displaystyle{ D = ((x + x) + x)x - (x + x)(x + x), }[/math] odakle je [math]\displaystyle{ D = - xx = - F^2. }[/math] Slično se provjeri za [math]\displaystyle{ T_3 = (2x, 3x, 5x) }[/math] pa se (1) lako dokaže matematičkom indukcijom.

Dakle, vrijedit će [math]\displaystyle{ D(T_1) = F^2, D(T_2) = - F^2, D(T_3) = F^2, ... }[/math]

Slučaj 2., [math]\displaystyle{ F_1 \lt F_2 }[/math]

Slično se dokazuje da u ovom slučaju vrijedi [math]\displaystyle{ D = F_1^2 - (F_1 + d)d. }[/math] Odavde vidimo da ako je [math]\displaystyle{ d \lt F_1 }[/math] će biti [math]\displaystyle{ D(T_{2k - 1})\gt 0, D(T_{2k}) \lt 0 }[/math] za [math]\displaystyle{ k \in \mathbb{N} }[/math], a ako je [math]\displaystyle{ d \gt F_1 }[/math] vrijedit će obratno.

Fibonnacijev niz u prirodi

Fibonaccijev niz se često povezuje i s brojem zlatnog reza fi (phi, [math]\displaystyle{ \varphi }[/math]), ili brojem kojeg mnogi zovu i "Božanskim omjerom". Uzmemo li jedan dio Fibonaccijevog niza, [math]\displaystyle{ 2, 3, 5, 8, }[/math] te podijelimo li svaki sljedeći broj s njemu prethodnim, dobiveni broj težit će broju fi: [math]\displaystyle{ \frac{3}{2} = 1, \frac{5}{3} = 1.67, \frac{8}{5} = 1.6, }[/math] itd. Broj [math]\displaystyle{ 1,618 }[/math] je fi zaokružen na tri decimale (fi je iracionalan). Odnosi mjera kod biljaka, životinja i ljudi, sa zapanjujućom preciznošću se približava broju fi.

Slijedi nekoliko primjera broja fi i njegove povezanosti sa Fibonaccijem i prirodom:

1. U pčelinjoj zajednici, košnici, uvijek je manji broj mužjaka pčela nego ženki pčela. Kada bi podijelili broj ženki sa brojem mužjaka pčela, uvijek bi dobili broj fi.
2. Nautilus (glavonožac), u svojoj konstrukciji ima spirale. Kada bi izračunali odnos svakog spiralnog promjera prema sljedećem dobili bi broj fi.
3. Sjeme suncokreta raste u suprotnim spiralama. Međusobni odnosi promjera rotacije je broj fi.
4. Izmjerimo li čovječju dužinu od vrha glave do poda, zatim to podijelimo s dužinom od pupka do poda, dobijamo broj fi.

Izvori

Nedovršeni članak Fibonaccijev broj koji govori o matematici treba dopuniti. Dopunite ga prema pravilima uređivanja Hrvatske internetske enciklopedije.