Bernsteinov polinom

Aproksimacija grafa funkcije upotrebom Bernsteinovog polinoma.

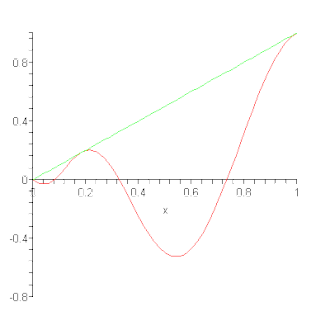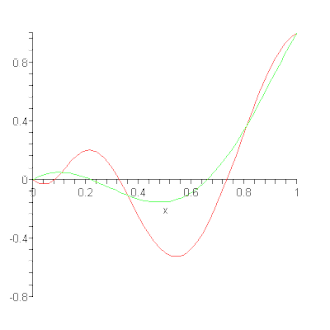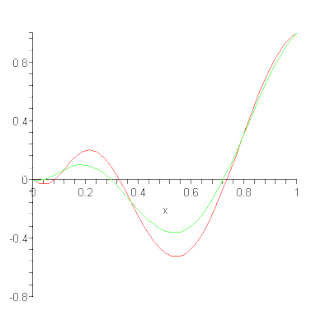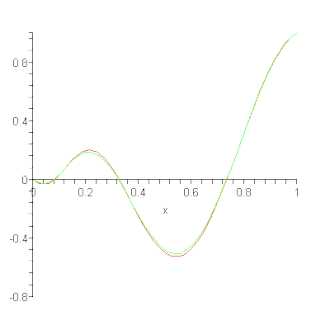
Bernsteinov polinom se može uzeti kao aproksimacija funkcije neprekidne na segmentu i to je polinom koji služi kao primjer za Weierstrassov teorem o aproksimaciji neprekidne funkcije na segmentu polinomom, koji govori da se razlika između funkcije i traženog polinoma (teorem ne daje metodu kako da se polinom nađe, nego samo utvrđuje postojanje) može napraviti proizvoljno malom, tj. $(\forall \epsilon >0)(|f(x)-P(x)|<\epsilon )$ gdje je P traženi polinom.

Bernsteinov polinom glasi (u slučaju segmenta $[0,1]$):

$\sum _{k=0}^{n}f\left({\frac {k}{n}}\right){\binom {n}{k}}x^{k}(1-x)^{n-k}$

Gdje je f funkcija neprekidna na segmentu realnih brojeva. Bernsteinov polinom se jednostavno izračunava: segment [0, 1] se podijeli na n jednakih dijelova i u dobivenim točkama $0,{\frac {1}{n}},{\frac {2}{n}},...,{\frac {n-1}{n}},1$ se računaju vrijednosti funkcije.

U slučaju segmenta $[a,b]$ Bernsteinov polinom glasi:

${\frac {1}{(b-a)^{n}}}\sum _{k=0}^{n}f\left(a+{\frac {k}{n}}(b-a)\right){\binom {n}{k}}(x-a)^{k}(b-x)^{n-k}$

Vidi još

• Binomni koeficijent