More actions
Bot: Automatski unos stranica |
m bnz |
||
| Redak 1: | Redak 1: | ||
[[datoteka:Perihelion precession.svg|mini|300px|desno|Prema [[Opća teorija relativnosti|Općoj teoriji relativnosti]], [[planet]] u svom obilasku oko [[Sunce|Sunca]] opisuje [[elipsa|elipsu]] koja se polako okreće u svojoj ravnini ([[Merkur]]ov zakret perihela).]] | |||
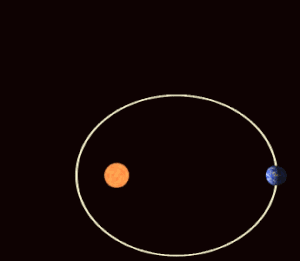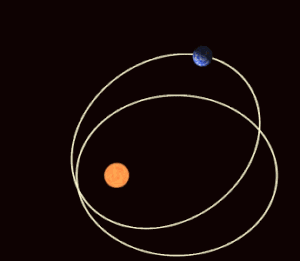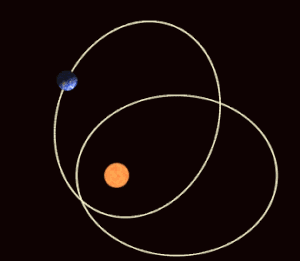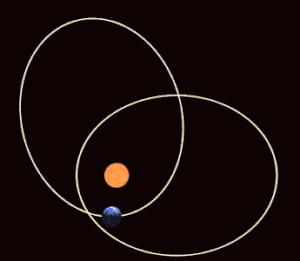
[[datoteka:Precessing Kepler orbit 280frames e0.6 smaller.gif|mini|300px|desno|Velika izduženost [[Merkur]]ove staze, s apsolutno najvećom [[brzina|brzinom]] putovanja od svih [[planet]]a, uzrok je jednom malom, [[Opća teorija relativnosti|relativističkom učinku]] prozvanom zakret perihela.]] | [[datoteka:Precessing Kepler orbit 280frames e0.6 smaller.gif|mini|300px|desno|Velika izduženost [[Merkur]]ove staze, s apsolutno najvećom [[brzina|brzinom]] putovanja od svih [[planet]]a, uzrok je jednom malom, [[Opća teorija relativnosti|relativističkom učinku]] prozvanom zakret perihela.]] | ||
Posljednja izmjena od 7. travanj 2022. u 13:23

Zakret perihela, apsidna precesija ili precesija perihela je vrsta precesije planetarne putanje. U 19. stoljeću opažene su promjene u Merkurovoj orbiti: točka u kojoj se Merkur najviše približava Suncu (perihel) zakretala se pomalo nakon svakog obilaska. Ova pojava nema objašnjenja u Newtonovoj klasičnoj mehanici i dugo se smatralo da postoji jedan nevidljiv planet, nazvan Vulkan, koji utječe na orbitu Merkura. Izmjereno odstupanje nije se moglo pripisati isključivo gravitacijskom utjecaju poznatih planeta. Pojavom Einsteinove teorije relativnosti pronađeno je objašnjenje za ova mala odstupanja. Zbog velike ekscentričnosti putanje, brzina Merkura se mijenja, a time i njegova masa (relativistički učinak). U tome se razlikovalo predviđanje klasične mehanike: Keplerovi zakoni predviđali su promjenu brzine planeta, ali su podrazumijevali stalnu masu. Ove promjene su male, ali izraženije kod Merkura nego kod drugih planeta, zbog njegove blizine Suncu.
Velika izduženost staze, s apsolutno najvećom brzinom putovanja od svih planeta, uzrok je jednom malom, relativističkom učinku prozvanom zakret perihela. Kada bi u okolini Sunca postojao samo Merkur, položaj velike osi njegove eliptične staze zakrenuo bi se u vlastitoj ravnini za kut 43,03″ u 100 godina. Učinak je predvidio Albert Einstein razrađujući relativističku teoriju gravitacije. Očit razlog učinka je u promjeni mase planeta pri promjeni brzine. Kako se u perihelu planet giba mnogo brže nego u afelu, a brzina gibanja je ionako velika, javlja se relativistička promjena mase. Osnovna pretpostavka klasične fizike planeta bila je u stabilnosti njihovih masa. Ako se masa mijenja, tijelo se neće oko Sunca gibati u stalnoj elipsi, već će se elipsa zakretati, i tijelo će opisivati rozetu. Osim relativističkog zakreta, staza Merkura zakreće se i zbog poremećaja ostalih planeta, pa se smjer velike osi elipse zakrene još za oko 500″ u 100 godina. Stvaran je zakret perihela jednak zbroju perturbacija i relativističkog učinka. Točnost astronomskih motrenja porasla je toliko da je utvrđeno kako je teorija relativističkog učinka točna bar na 1%, ako ne i bolje.[1]
Merkurov zakret perihela
Prema Einsteinevoj Posebnoj teoriji relativnosti nijedno se djelovanje, odnosno signal, ne može prenositi brže od brzine svjetlosti, pa je stoga Newtonova teorija gravitacije u neskladu sa posebnom teorijom relativnosti. Prema Newtonovoj teoriji, planet u svom obilasku oko Sunca opisuje elipsu koja miruje u koordinatnom sustavu Sunca usmjerenom prema dalekim svemirskim objektima. Prema Općoj teoriji relativnosti, ta se elipsa polako okreće u svojoj ravnini. Točnije rečeno, planet zapravo opisuje krivulju poput rozete. To se očituje tako da se Suncu najbliža točka staze ili perihel, pomalo pomiče. Taj je pomak to veći što je planet bliži Suncu, i to se točnije može odrediti što je veći eskcentricitet elipse (omjer udaljenosti žarišta elipse od središta prema velikoj poluosi). Od Sunčevih planeta Merkur je najbliži Suncu i ima najveći iznos eskcentriciteta elipse 0,2056, za Veneru je 0,0068 a za Zemlju 0,0167. Stoga je pomicanje Merkurova perihela najveće i može se najtočnije odrediti. Prema Općoj teoriji relativnosti treba da iznosi 575 lučnih sekundi u stoljeću (to je maleni kut pod kojim se vidi kovani novčić na udaljenosti od otprilike 100 metara).
Prema klasičnoj Newtonovoj teoriji, kut pomicanja Merkurova perihela bi bio 0 (nula) kada bi Merkur bio jedini planet. No, zbog smetnji drugih planeta, najviše Venere, Zemlje i Jupitera, trebalo bi i prema Newtonovoj teoriji nastati pomicanje Merkurova perihela, otprilike za 532 lučne sekunde u stoljeću. No, opažanja daju više, pa vrijednost razilaženja opažanja i klasičnog računa, uzevši u obzir sve potrebne korekcije, iznosi 43.11 ± 0.45″, što se izvrsno slaže sa spomenutim iznosom koji zahtijeva Einsteinova teorija. Pri tom se smetnje drugih planeta računaju prema Newtonovoj teoriji, jer bi njihova relativistička korekcija bila reda veličine 0,0001 lučnih sekundi u stoljeću, što dakako izmiče mogućnosti opažanja. Za Veneru i Zemlju rezultati opažanja se dobro slažu s Einstinovom teorijom, dok je relativistički pomak perihela za ostale planete premalen, a da bi se dao pouzdano izmjeriti.[2]
Einsteinovo objašnjenje
Merkurov zakret perihela je prvi zabilježio Urbain Le Verrier sredinom 19. stoljeća, a prvi ju je matematički izrazio Albert Einstein u općoj teoriji relativnosti. Einstein je pokazao da za planet, kojoj je velika poluos elipse α (planetarna putanja), i ekscentricitet putanje e, a ophodno vrijeme T, onda je zakret perihela zbog tog relativističkog učinka ε, za vrijeme jednog ophoda oko Sunca, u radijanima je:
gdje je: c - brzina svjetlosti. Kod Merkura, velika poluos elipse je oko 57.9 milijuna kilometara ili 57,9 · 109 m, ekscentricitet putanje je 0,206 i ophodno vrijeme je 87,97 dana, ili 7,6 · 106 sekundi. Osim toga, brzina svjetlosti je 3∙108 m/s, pa se Merkurov zakret perihela za vrijeme jednog ophoda ono Sunca može izračunati kao = 5,028 · 10−7 radijana, 2,88 · 10−5 ° ili 0,104". U 100 godina, Merkur napravi oko 415 ophoda ili obilazaka oko Sunca, pa Merkurov zakret perihela u 100 godina iznosi oko 43″, što je gotovo točno izmjerenim podatcima kod mjerenja. [3]
Zakret perihela Zemlje
S vremenom se mijenja i položaj Zemljine staze u ravnini gibanja, pa godišnji progradni zakret perihela (pomicanje u smjeru ophoda oko Sunca), potaknut utjecajem planeta i relativističkim učinkom, iznosi 11,63″. [4] Period Zemljinog zakreta perihela u odnosu na zvijezde je 112 000 godina.[5]
Milankovićevi ciklusi
Milutin Milanković je otkrio da su periodične promjene ekscentriciteta Zemljine putanje i nagiba Zemljine osi uzrok dugoročnih klimatskih promjena, to jest nastanka i nestanka ledenih doba, koji su nazvani Milankovićevi ciklusi. Ustanovio je osnovni period od približno 100 000 godina i sekundarne periode od približno 400 000 i 125 000 godina, u kojima zbog promjene ekscentriciteta Zemljine putanje nastaju značajne promjene primljene količine Sunčeva zračenja. Osim toga našao je i period promjene nagiba Zemljine osi od približno 41 000 godina, koji dovodi do smanjenja Sunčeva zračenja u višim zemljopisnim širinama.
Trenutno Zemlja prolazi kroz perihel svake godine zimi, 3. siječnja, a kroz afel ljeti, 4. srpnja. Time se ublažava klima na sjevernoj polutki: ljeta su duža i manje vruća, a zime su kraće i blaže. Na južnoj polutci vladaju suprotni uvjeti. Kombinacijom utjecaja zakreta perihela i precesije Zemljine osi za 13 000 godina doći će do toga da će Zemlja prolaziti kroz perihel sredinom ljeta na sjevernoj polutki, te će klimatski utjecaji biti obratni.[5]
Izvori
- ↑ Vladis Vujnović : "Astronomija", Školska knjiga, 1989.
- ↑ "Tehnička enciklopedija", glavni urednik Hrvoje Požar, Grafički zavod Hrvatske, 1987.
- ↑ Stephen Hawking: "On the Shoulders of Giants : the Great Works of Physics and Astronomy", pages = 1243, "Foundation of the General Relativity" (translated from Albert Einstein's "Die Grundlage der Allgemeine Relativitätstheorie", first published in 1916 in "Annalen der Physik", volume 49), Running Press, Philadelphia, Pennsylvania, USA
- ↑ Zemlja, [1] "Hrvatska enciklopedija", Leksikografski zavod Miroslav Krleža, www.enciklopedija.hr, 2014.
- ↑ 5,0 5,1 Milankovitch (Orbital) Cycles and Their Role in Earth's Climate, NASA. Pristupljeno 10. 12. 2020. (engl.)

