Descartesov oval

Primjer Descartesovog ovala

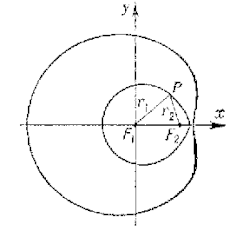
Descartesov oval ili Kartezijev oval je ravninska algebarska krivulja četvrtoga reda. Descartes tu krivulju prvi puta promatra 1637. godine u vezi sa sljedećom zadaćom iz optike: odrediti vrstu krivulje na kojoj se zrake koje izlaze iz jedne dane točke lome tako, da nakon loma prolaze kroz drugu danu točku. No ove krivulje je proučavao i Isaac Newton početkom 1664.

Ta krivulja ima svojstvo da udaljenosti $r_{1},r_{2}$ bilo koje njezine točke $P$ od dviju čvrstih točaka $F_{1},F_{2}$ žarišta povezuje jednakost $r_{1}+mr_{2}=a$ gdje su $a,m$ konstante. Drugim riječima, Descartesov oval dobivamo linearnom kombinacijom $r_{1},r_{2}$.

Za $m=1$ dobiva se elipsa, a za $m=-1$ se dobiva hiperbola. Poseban slučaj ove krivulje je i Pascalov puž.