Pascalov puž

Primjeri Pascalovih puževa

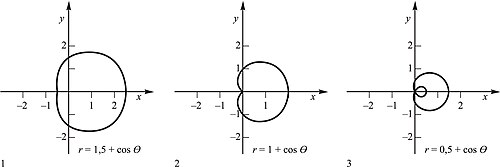
Pascalov puž ili Limacon (nazvan po Étienneu Pascalu (1588. – 1651.), ocu Blaisea Pascala) je konhoida kružnice, algebarska ravninska krivulja četvrtoga reda koja nastaje kada se s vanjske strane produlji ili skrati radijvektor kružnice koji vrškom ispisuje krivulju dok jedna kružnica obilazi drugu, jednaku kružnicu. U pravokutnom Kartezijevu koordinatnom sustavu određena je jednadžbom: [math]\displaystyle{ (x^2+y^2-ax)^2=l^2(x^2+y^2). }[/math], u polarnom koordinatnom sustavu jednadžbom [math]\displaystyle{ r = a\cos{\theta} + l }[/math], gdje je [math]\displaystyle{ a }[/math] promjer kružnice, a l udaljenost krivulje od kružnice za [math]\displaystyle{ y = 0 }[/math]. Poseban je slučaj Pascalova puža, kada je [math]\displaystyle{ a = l }[/math], kardioida. Površina Pascalova puža dana je formulom: [math]\displaystyle{ P = \frac{(\pi a^2)}{2} + l^2\pi }[/math]; u slučaju kad je [math]\displaystyle{ a \gt l }[/math] površina unutarnje petlje računa se dvaput.