Mehanika kontakta
Mehanika kontakta bavi se računanjem elastičnih, viskoelastičnih ili plastičnih tijela pri statičnom ili dinamičnom kontaktu. Mehanika kontakta je osnovna strojarsko-znanstvena disciplina, neophodna za siguran i energetski štedljiv koncept tehničkih postrojenja.
Ona je od interesa za primjenu kod, na primjer, kontakta između točaka i željezničkog kolosijeka, kod spojki, kočnica, guma, kliznih i kugličnih ležajeva, motora sa unutrašnjim izgaranjem, zglobova, hermetizacije, oblikovanja materijala, ultrazvučnog zavarivanja, električnih kontakata i mnogih drugih. Njeni zadaci obuhvatačaju dokaz čvrstine kontaktnih i spojnih elemenata, preko utjecaja podmazivanja ili dizajna materiala na trenje i habanje pa sve do primjene u sistemima mikro i nanotehnike.
Povijest
Klasična mehanika kontakta je prvenstveno povezana sa Heinrichom Hertzom. 1882. godine Hertz je riješio problem kontakta između dva elastična tijela sa zakrivljenim površinama. Ovaj klasični rezultat predstavlja i danas jedan temelj mehanike kontakta. Tek nepuno stoljeće kasnije pronašli su Johnson, Kendall i Roberts slično rješenje za adhezivni kontakt (JKR-Teorija).
Sljedeći napredak znanja o mehanici kontaka ostvaren je sredinom 20. stoljeća zahvaljujući Bowdenu i Taboru. Oni su prvi ukazali na važnost hrapavosti kontaktnih tijela. Hrapavost utječe na to da je stvarna površina kontakta između tijela, između kojih se ostvaruje trenje, po pravilu za red veličine manja u odnosu na prividnu površinu kontakta. Ovo saznanje munjevito je izmjenilo i pravac mnogih tribologičnih istraživanja. Radovi Bowdena i Tabora prouzrokovali su čitav niz teorija mehanike kontakta hrapavih površina.
Kao pionirske radove na ovom području treba prije svega spomenuti radove Archarda (1957.), koji na kraju zaključuje da je i u kontaktu elastičnih hrapavih površina kontaktna površina približno proporcionalna normalnoj sili. Sljedeći važni prilozi povezani su sa imenima Greenwooda i Williamsona (1966.), Busha (1975.) i Perssona (2002.). Najvažniji rezultat ovih radova je da je stvarna kontaktna površina kod hrapavih površina grubo proporcionalna normalnoj sili, dok su uvjeti u pojedinačnim mikrokontaktima (pritisak, veličina mikrokontakta) samo slabo zavisni od opterećenja.
Klasični zadaci u kontaktnoj mehanici
Kontakt između kugle i elastičnog poluprostora
Promatrajno elastičnu kuglu polumjera [math]\displaystyle{ R }[/math] utisnutu u elastični prostor za veličinu [math]\displaystyle{ d }[/math] (veličina udubljenja). Pri tome se obrazuje kontaktno područje polumjera [math]\displaystyle{ a=\sqrt{Rd} }[/math]. Za to je potrebna sila
[math]\displaystyle{ F=\frac{4}{3}E^*R^{1/2}d^{3/2} }[/math] ,
pri čemu
[math]\displaystyle{ \frac{1}{E^*}=\frac{1-\nu^2_1}{E_1}+\frac{1-\nu^2_2}{E_2} }[/math] .
gdje su [math]\displaystyle{ E_1 }[/math] i [math]\displaystyle{ E_2 }[/math] moduli elastičnosti a [math]\displaystyle{ \nu_1 }[/math] i [math]\displaystyle{ \nu_2 }[/math] poissonove konstante oba tijela.
Neka su dvije kugle polumjera [math]\displaystyle{ R_1 }[/math] i [math]\displaystyle{ R_2 }[/math] u kontaktu. Tada ove jednadžbe važe i dalje, s tim što je polumjer [math]\displaystyle{ R }[/math]
[math]\displaystyle{ \frac{1}{R}=\frac{1}{R_1}+\frac{1}{R_2} }[/math].
Raspodjela pritiska u kontaktnom području je data kao
[math]\displaystyle{ p=p_0\left(1-\frac{r^2}{a^2}\right)^{1/2} }[/math]
sa
[math]\displaystyle{ p_0=\frac{2}{\pi}E^*\left(\frac{d}{R}\right)^{1/2} }[/math].
Maksimalan smičući napon za [math]\displaystyle{ \nu = 0,33 }[/math] je pri[math]\displaystyle{ z\approx 0,49a }[/math] .
Kontakt između dva ukrštena cilindra istih polumjera [math]\displaystyle{ R }[/math]
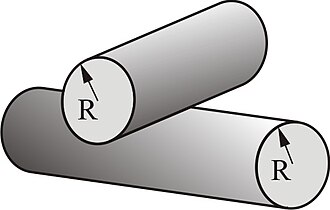
je isti kao i kontakt kugle polumjera [math]\displaystyle{ R }[/math] i ravnine (pogledaj gore).
Kontakt između tvrdog cilindra i elastičnog poluprostora
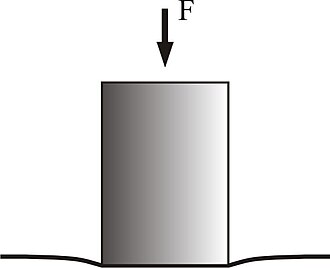
Jedan tvrdi cilindrični pečat polumjera [math]\displaystyle{ a }[/math] utisnut u elastični poluprostor stvara sljedeću raspodjelu pritiska
[math]\displaystyle{ p=p_0\left(1-\frac{r^2}{a^2}\right)^{-1/2} }[/math]
sa
[math]\displaystyle{ p_0=\frac{1}{\pi}E^*\frac{d}{a} }[/math].
Povezanost između veličine udubljenja [math]\displaystyle{ d }[/math] i normalne sile je data kao
[math]\displaystyle{ F=2aE^*d\frac{}{} }[/math].
Kontakt između tvrdog koničnog utiskivača i elastičnog poluprostora
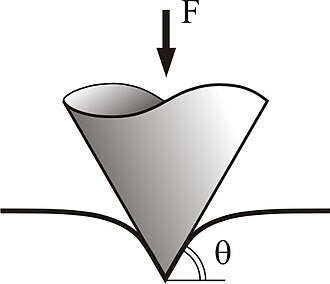
Kod utiskivanja tvrdog koničnog utiskivača u elastični poluprostor postoji sledeća povezanost između veličine udubljenja [math]\displaystyle{ d }[/math] i kontaktnog polumjera [math]\displaystyle{ a }[/math]
[math]\displaystyle{ d=\frac{\pi}{2}a\tan\theta }[/math]
[math]\displaystyle{ \theta }[/math] je ugao između granične ravnine poluprostora i izvodnice konusa. Raspodjela pritiska je opisana sljedećom jednadžbom
[math]\displaystyle{ p(r)=-\frac{Ed}{\pi a\left(1-\nu^2\right)}ln\left(\frac{a}{r}+\sqrt{\left(\frac{a}{r}\right)^2-1}\right) }[/math] .
Napon u vrhu konusa (u centru kontaktnog područja) ima logaritmički singularitet. Ukupna sila određuje se prema
[math]\displaystyle{ F_N=\frac{2}{\pi}E\frac{d^2}{\tan \theta} }[/math].
Kontakt između dva cilindra sa paralelnim osima
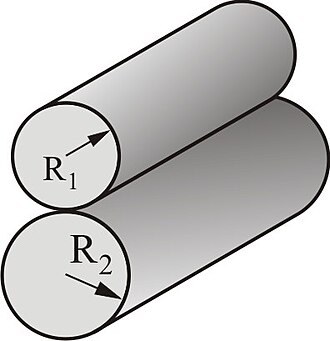
Sila je kod kontakta između dva cilindra sa paralelnim osima linearno proporcionalna veličini udubljenja
[math]\displaystyle{ F=\frac{\pi}{4}E^*Ld }[/math].
Polumjer zakrivljenja se u ovoj relaciji ne pojavljuje. Polovina kontaktne širine je data kao
[math]\displaystyle{ a=\sqrt{Rd} }[/math] ,
sa
[math]\displaystyle{ \frac{1}{R}=\frac{1}{R_1}+\frac{1}{R_2} }[/math]
i ista je kao i u kontaktu između dvije kugle. Maksimalni pritisak je
[math]\displaystyle{ p_0=\left(\frac{E^*F}{\pi LR}\right)^{1/2} }[/math] .
Kontakt između hrapavih površina
Kod kontakta između dva tijela sa hrapavim površinama je stvarna površina kontakta [math]\displaystyle{ A }[/math] mnogo manja nego prividna površina kontakta [math]\displaystyle{ A_0 }[/math] . Stvarna površina kontakta između stohastički hrapave površine i elastičnog poluprostora je proporcionalna normalnoj sili [math]\displaystyle{ F }[/math] i data je kroz jednadžbu
[math]\displaystyle{ A=\frac{\kappa}{E^*h'}F }[/math]
Pri čemu je [math]\displaystyle{ h' }[/math] srednja kvadratna vrijednost nagiba površine i [math]\displaystyle{ \kappa \approx2 }[/math]. Srednji pritisak u stvarnoj površini kontakta
[math]\displaystyle{ \sigma =\frac{F}{A}\approx\frac{1}{2}E^*h' }[/math]
računa se približno kao polovina efektivnog elastičnog modula [math]\displaystyle{ E^* }[/math] pomnožena srednjom kvadratnom vrijednosti nagiba [math]\displaystyle{ h' }[/math] profila površine. Ako je ovaj pritisak veći od tvrdoće materiala [math]\displaystyle{ \sigma _0 }[/math], što znači
[math]\displaystyle{ \Psi = \frac{E^*h'}{\sigma _0}\gt 2 }[/math],
onda je mikrohrapavost potpuno u plastičnom stanju. Za [math]\displaystyle{ \Psi \lt \frac{2}{3} }[/math] površina se pri kontaktu ponaša elastično. Veličinu [math]\displaystyle{ \Psi }[/math] su Greenwood i Williamson uveli i zove se indeks plastičnosti. Da li se sistem elastično ili plastično ponaša ne zavisi od primijenjene normalne sile.
Literatura
- K. L. Johnson: Contact mechanics. Cambridge University Press, 6. Nachdruck der 1. Auflage, 2001.
- Popov, Valentin L.: Kontaktmechanik und Reibung. Ein Lehr- und Anwendungsbuch von der Nanotribologie bis zur numerischen Simulation, Springer-Verlag, 2009, 328 S., ISBN 978-3-540-88836-9.
- Popov, Valentin L.: Contact Mechanics and Friction. Physical Principles and Applications, Springer-Verlag, 2010, 362 p., ISBN 978-3-642-10802-0.
- I. N. Sneddon: The Relation between Load and Penetration in the Axisymmetric Boussinesq Problem for a Punch of Arbitrary Profile. Int. J. Eng. Sci.,1965, v. 3, pp. 47–57.
- S. Hyun, M.O. Robbins: Elastic contact between rough surfaces: Effect of roughness at large and small wavelengths. Trobology International, 2007, v.40, pp. 1413-1422.