Komplement skupa
Komplement je u teoriji skupova onaj skup koji promatranom skupu činu takvu dopunu da njih dvoje skupa čine univerzalni skup. Primjer je univerzalni skup prirodnih brojeva u kojem je skup neparnih brojeva komplement skupu parnih brojeva.[1]
Dva se skupa također mogu "oduzeti". Relativni komplement skupa A u skupu B (još se koristi i naziv skupovna razlika skupova B i A), označeno sa B − A, (ili B \ A), je skup svih elemenata koji su članovi skupa B, ali nisu članovi skupa A. Potrebno je uočiti da je valjana operacija "oduzimanja" članova koji nisu u skupu, poput micanja elementa zelena iz skupa {1,2,3} - takva operacija nema učinka.
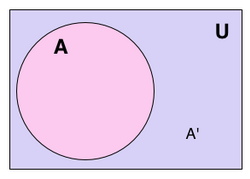
U određenim postavkama, svi skupovi koji se promatraju, smatraju se podskupovima nekog danog univerzalnog skupa U. U takvim slučajevima, U − A zove se apsolutni komplement ili jednostavno komplement skupa A, i označava s A′, AC ili .
Primjeri:
- {1, 2} − {crvena, bijela} = {1, 2}
- {1, 2, zelena} − {crvena, bijela, zelena} = {1, 2}
- {1, 2} − {1, 2} = ø
- Ako je U skup svih cijelih brojeva, P skup parnih brojeva, a N skup svih neparnih brojeva, tada komplement skupa P u U iznosi N, ili ekvivalentno, P′ = N.
Neka osnovna svojstva komplementa:
- A U A′ = U
- A ∩ A′ = ø
- (A′ )′ = A
- A − A = ø
- A − B = A ∩ B′
Izvori
- ↑ Leksikon matematike / <prijevod Predrag Raos>, Zagreb : Mozaik knjiga, <2001?> Prijevod djela: The Hutchinson Pocket Dictionary of Maths (Helicon Publishing, 1993), str. 55