San brucoša: razlika između inačica
Prijeđi na navigaciju
Prijeđi na pretraživanje
m bnz |
m file->datoteka |
||
| Redak 1: | Redak 1: | ||
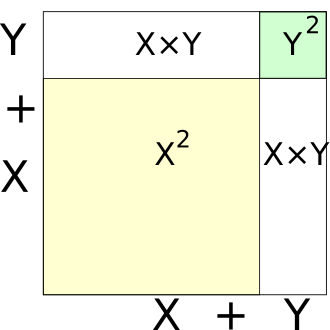
San brucoša''' je termin koji se često prirodaje sljedećoj greški u računanju ''n''-te potencije binoma: <math>(x + y)^n = x^n + y^n. </math> Naziva se tako jer [[student]]i prve godine nerijetko zaboravljaju ispravan razvoj kvadrata binoma koji se uči još u [[Osnovna škola|osnovnoj školi]] pa tako računaju <math>(x + y)^2 = x^2 + y^2,</math> što prema [[Binomni poučak|binomnon teoremu]] ne vrijedi, nego je ispravno pisati <math>(x + y)^2 = x^2 + 2xy + y^2.</math> | San brucoša''' je termin koji se često prirodaje sljedećoj greški u računanju ''n''-te potencije binoma: <math>(x + y)^n = x^n + y^n. </math> Naziva se tako jer [[student]]i prve godine nerijetko zaboravljaju ispravan razvoj kvadrata binoma koji se uči još u [[Osnovna škola|osnovnoj školi]] pa tako računaju <math>(x + y)^2 = x^2 + y^2,</math> što prema [[Binomni poučak|binomnon teoremu]] ne vrijedi, nego je ispravno pisati <math>(x + y)^2 = x^2 + 2xy + y^2.</math> | ||
[[ | [[Datoteka:Freshman's Dream.svg|right|thumbnail|U istinitost binomnog teorema za slučaj n = 2 možemo se uvjeriti ovom skicom.]] | ||
== Zanimljivosti == | == Zanimljivosti == | ||
Posljednja izmjena od 8. svibanj 2022. u 03:46
San brucoša je termin koji se često prirodaje sljedećoj greški u računanju n-te potencije binoma: Naziva se tako jer studenti prve godine nerijetko zaboravljaju ispravan razvoj kvadrata binoma koji se uči još u osnovnoj školi pa tako računaju što prema binomnon teoremu ne vrijedi, nego je ispravno pisati
Zanimljivosti
Zanimljivo je da postoji sličan identitet koji vrijedi za svaka dva cijela broja i za svaki neparni prosti broj
Naime, prema Malom Fermatovom teoremu vrijedi a isto tako je . Sada lagano slijedi te koristeći svojstvo tranzitivnosti modula zaista dobivamo da je [1]
Izvori
- ↑ http://www.mathos.unios.hr › ...PDF Kvadratni zakon reciprociteta - Odjel za matematiku









