Razlika između inačica stranice »Simetrična razlika skupova«
Izvor: Hrvatska internetska enciklopedija
m (bny) |
m (file->datoteka) |
||
| Redak 1: | Redak 1: | ||
[[ | [[Datoteka:Venn0110.svg|thumb| | ||
[[Vennov dijagram]] <math>A \triangle B</math>. Simetrična razlika je unija bez (vidi relativni komplement) presjeka: | [[Vennov dijagram]] <math>A \triangle B</math>. Simetrična razlika je unija bez (vidi relativni komplement) presjeka: | ||
{{nowrap|[[ | {{nowrap|[[Datoteka:Venn0111.svg|40px]] <math>~\setminus~</math> [[Datoteka:Venn0001.svg|40px]]}} <math>~=~</math> [[Datoteka:Venn0110.svg|40px]] | ||
]] | ]] | ||
Trenutačna izmjena od 06:42, 8. svibnja 2022.
Vennov dijagram [math]\displaystyle{ A \triangle B }[/math]. Simetrična razlika je unija bez (vidi relativni komplement) presjeka: 
[math]\displaystyle{ ~\setminus~ }[/math] 
[math]\displaystyle{ ~=~ }[/math] 
[math]\displaystyle{ ~\setminus~ }[/math] 
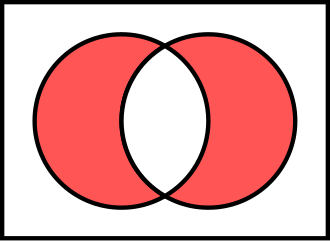
[math]\displaystyle{ ~=~ }[/math] Simetrična razlika odnosno disjunktivna unija (uobičajeni simboli :[math]\displaystyle{ \triangle\ , \ominus , \oplus }[/math]) u n skupova u teoriji skupova jest unija razlike n zadanih skupova. Dobiveni skup dobiven je primjenom operacije simetrične razlike na njima.[1]
[math]\displaystyle{ A \triangle B=(A\setminus B)\cup (B\setminus A ) }[/math]
Primjer:
[math]\displaystyle{ \{1,2,3\} \triangle \{3,4\} = \{1,2,4\} }[/math].
Disjunktivna unija nije isto što i disjunktna unija.